Виды пропорциональных отношений

ЛЕКЦИЯ 6

Средства гармонизации формы

ПРОПОРЦИИ

Понятие о пропорции в архитектуре

Одним из важнейших методов построения выразительной и целостной ар­хитектурной формы является пропорционирование.

Пропорция (лат. proportio) - соразмерность, определенное соотношение частей между собой. В современной литературе понятие пропорции употребляет­ся в трехосновных значениях:

1. Наиболее близкое к понятию соразмерности. Означает соотношение основных параметров формы (длина, ширина, высота). Именно это значение имеют в виду, когда говорят о пропорциях какого-либо зда­ния, сооружения. Пропорция здесь характеризует объект как целое, составляет основу его образа.

2. Под пропорцией в архитектуре (так же как и математике) понимают ра­венство отношений количественной меры одних и тех же объективных свойств в сопоставляемых формах или их частях. В математической форме записывают как а/в = c/d. Это значение понятия «пропорция» используется в большинстве работ, посвященных пропорционированию в архитектуре. Из математической записи та­кого понимания следует, что здесь в основе образования целостной формы лежит принцип геометрического подобия. Наиболее распространенным в архитектуре примером применения пропорции как равенства математических отношений яв­ляется образование формы на основе подобных прямоугольников, диагонали ко­торых либо параллельны (прямая пропорция), либо перпендикулярны (обратная пропорция) (рис. 33).

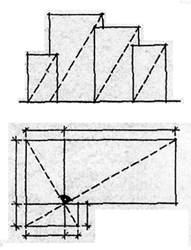Рис. 33

Виды пропорций на основе подобных прямоугольников

Пропорцию, средние члены которой равны между собой, называют непре­рывной. Примером непрерывной пропорции может служить ряд подобных прямоугольников, в котором длина предыдущего прямоугольника равна ширине после­дующего.

3. Под пропорцией в архитектуре понимают любую закономерность в соот­ношениях величин, которая связывает отдельные части и параметры формы в единое целое (наиболее правильное определение). Таким образом, пропорция в архитектуре есть понятие, отражающее однородность (закономерность) измене­ний количественной меры при переходах от одной части формы к другой и к фор­ме в целом.

Первое и второе определения пропорции являются частными случаями по­следнего определения.

Виды пропорциональных отношений

В теории и практике архитектуры хорошо известны такие виды закономер­ных (однородных) изменений величин, как арифметическая гармоническая и гео­метрическая прогрессии.

Арифметическая прогрессия выражается рядом чисел, в котором каждое

последующее число больше предыдущего на одну и ту же величину. Простейшим примером арифметической прогрессии является ряд натуральных чисел 0, 1,2, 3, 4, 5 и т.д.

Гармоническая прогрессия - это ряд чисел обратных ряду чисел арифме­тической прогрессии, например: 1/2, 1/3, 1/4, 1/5, 1/6, 1/7. Отношения между сосед­ними членами гармонического ряда по мере его возрастания так же, как и в ариф­метической прогрессии, изменяются от контрастных к нюансным.

Геометрическая прогрессия представляет собой ряд чисел, в котором каж­дое последующее число больше (или меньше) предыдущего в одно и то же число
раз. Например: 1,2,4,8,16,...: 1, 1/2, 1/4, 1/8, 1/16.

Широко используются в архитектуре аддитивные ряды, построенные на суммировании чисел. Например, в ряде чисел 1, 2, 3, 5, 8, 13, 21, 34,...(ряд Фибо­наччи) каждый последующий член, начиная с 3-го равен сумме двух предыдущих. Отношение между смежными членами такого ряда, начиная с 5-го члена, практи­чески постоянно и равно 1,62.

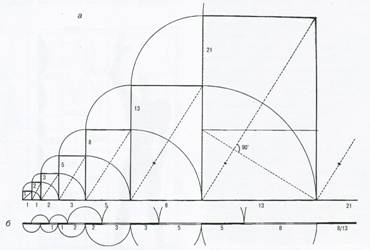Рис. 34 Линейная и двухмерная интерпретация ряда Фибоначчи: а – двухмерная – прямоугольники, начиная с 8:13, 13:21, приобретают пропорции «золотого сечения» и взаимное подобие – их диагонали параллельны и взаимоперпендикулярны; б – линейная - стабилизация пропорций «золотого сечения», начиная от 3:5:8; 5:8:13…