Логарифмическая функция.
Просмотреть видеоурок https://resh.edu.ru/subject/lesson/3834/main/198660/
Написать конспект
Перечень вопросов, рассматриваемых в теме
1) Понятие логарифмической функции
2) Свойства логарифмической функции
3) График логарифмической функции
Глоссарий по теме
Логарифмическая функция. Ф ункция вида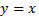 
, где a – заданное число, a > 0, a ≠ 1.
Свойства логарифмической функции:
1. Область определения – множество всех положительных чисел.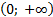 
2. Множество значений логарифмической функции – множество всех действительных чисел.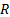 
3. Неограниченная функция.
4. Возрастающая, если a > 1, и убывающая, если 0 < a < 1.
5. Нули функции: х = 1 (т. к.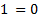 
)
6. Промежутки знакопостоянства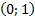 
и 
.
Если a > 0, то функция принимает положительные значение при х > 1, отрицательные при 0 < x < 1.
Если0 < a < 1, функция принимает положительные значение при 0 < х < 1, отрицательные при x > 1.
Открытые электронные ресурсы:
https://fipi.ru/
Теоретический материал для самостоятельного изучения
В математике и других науках достаточно часто встречаются функции, содержащие логарифм.
Функцию вида 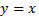, где a – заданное число, a > 0, a ≠ 1 называют логарифмической функцией.
Свойства логарифмической функции:
1. Область определения – множество всех положительных чисел. 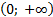. Это следует из определения логарифма (т. к. логарифм существует только положительного числа!)
2. Множество значений логарифмической функции – множество всех действительных чисел.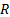
3. Неограниченная функция. (Следует напрямую из 2 свойства.)
4. Возрастающая, если a > 1, и убывающая, если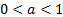 
.
Докажем возрастание по определению возрастающей функции, если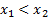 
, то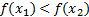 
.
Пусть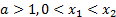 
.
По основному логарифмическому тождеству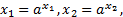 
cследовательно 
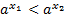. По свойству степеней с одинаковым основанием, большим 1 имеем: 
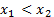. Т. е. большему значению аргумента соответствует большее значение функции, следовательно, функция возрастающая. Аналогично доказывается убывание функции при основании .
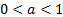Из этого свойства следуют два важных утверждения:
Если a > 0 и 
Если 0 < a < 1 и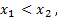 
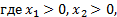
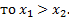
5. Нули функции: х = 1 (т. к. )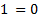
6. Промежутки знакопостоянства 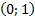и .
Если a > 0, то функция принимает положительные значение при х > 1, отрицательные при 0 < x < 1.
Если0 < a < 1, функция принимает положительные значение при 0 < х < 1, отрицательные при x > 1.
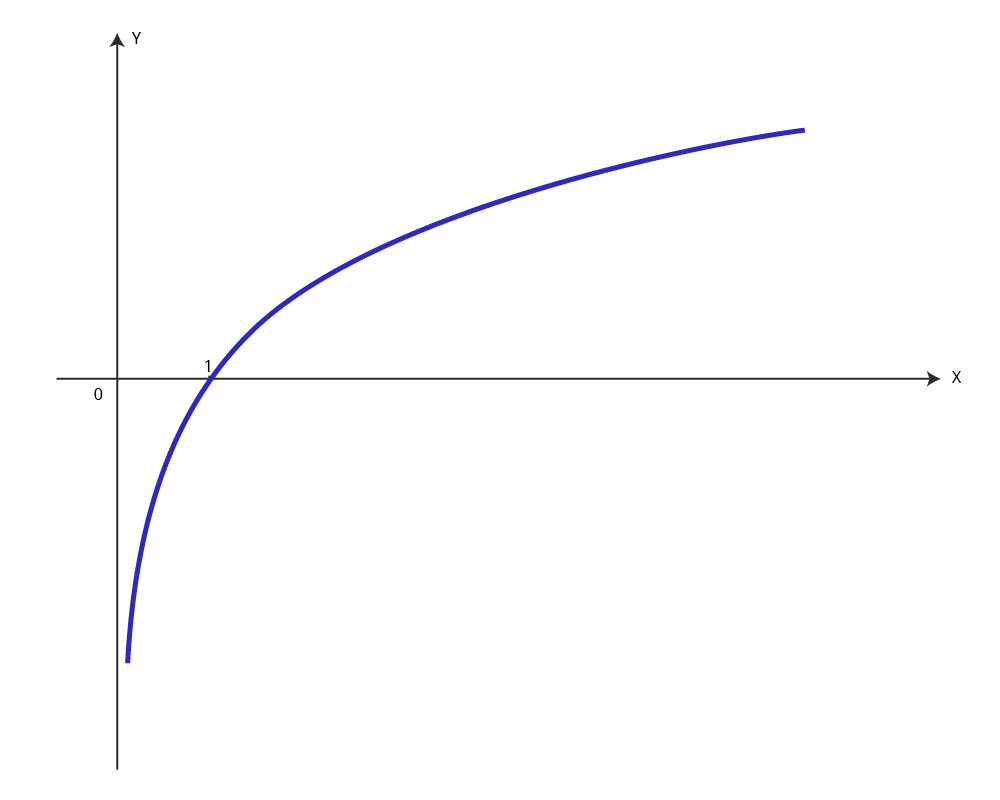
Из рассмотренных свойств логарифмической функции следует, что ее график располагается правее оси Оу, обязательно проходит через точку (1; 0) и имеет вид: если основание больше 1 (график №1) и если основание больше нуля, но меньше 1 (график №2).
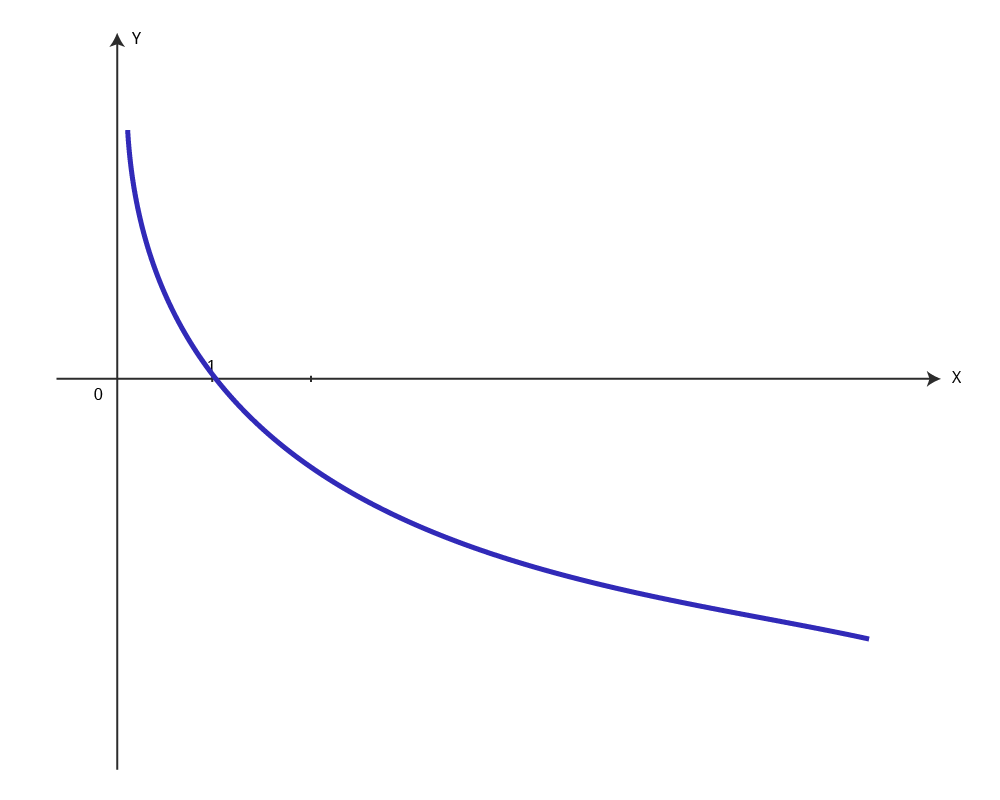
Отметим, если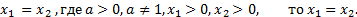 
Докажем это утверждение.
Предположим, что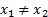 
, например, 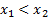. Тогда если основание 
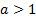, в силу возрастания функции 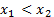. Противоречие с условием задачи. Если 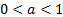, тогда функция убывающая и 
. Тоже противоречие с условием задачи, что 
. Следовательно, 
.
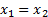Это свойство применяется при решении уравнений.
Задача 1.
Решить уравнение: 
Слева и справа логарифмы по одинаковым основаниям, значит при условии, что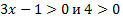 
(иначе логарифмы не существуют) приравниваем выражения под логарифмами: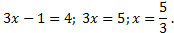 
Ответ: 
.
Особенности графиков логарифмической функции с разными основаниями.
Построим в одной системе координат графики функций 
; 
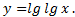
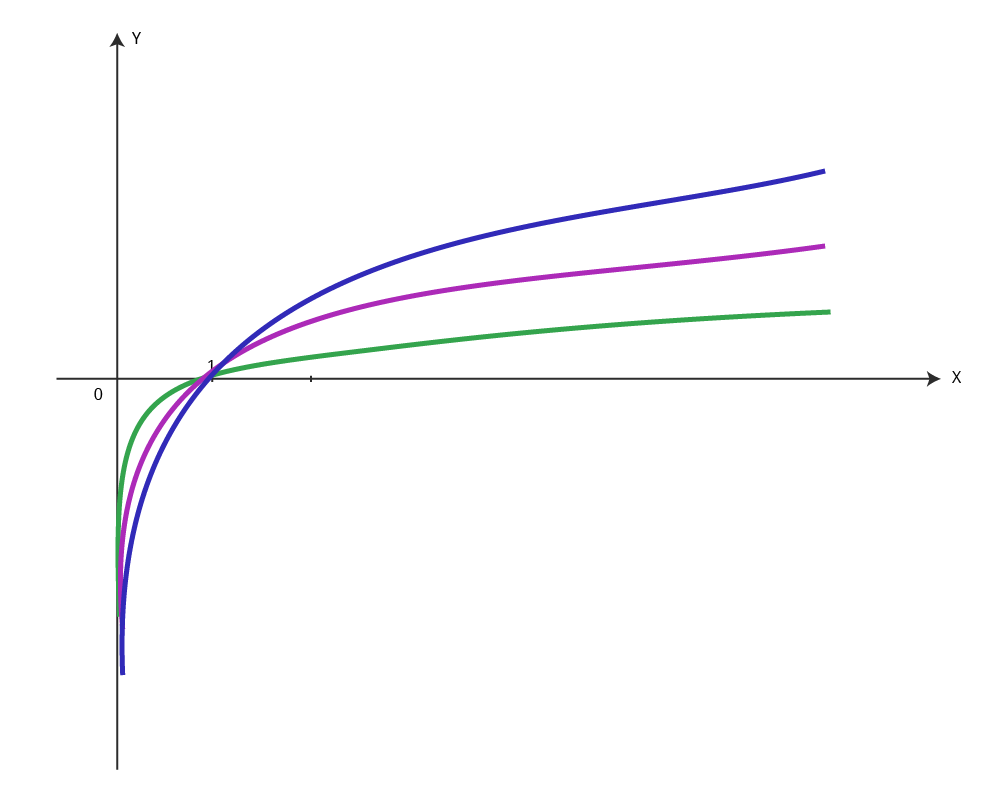
Видно, что чем больше основание, тем ближе к осям координат расположен график. Обратите внимание: все графики проходят через точку (1; 0).
В другой системе координат построим графики функций с основаниями от 0 до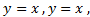 
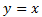
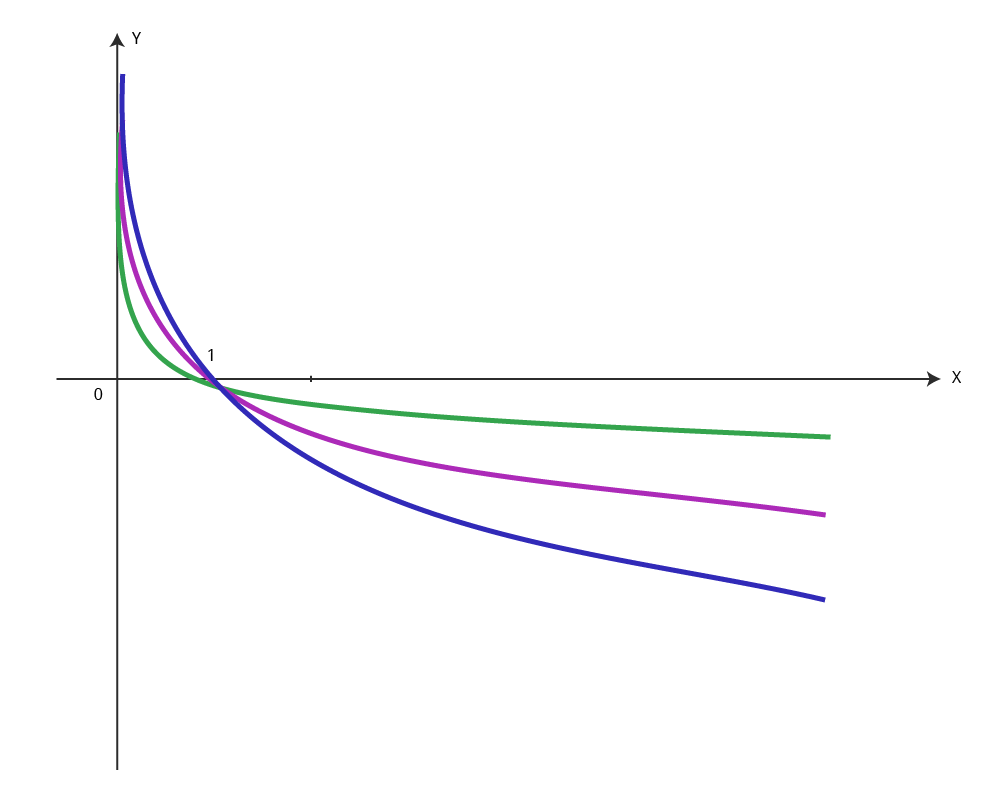
Видно, что в этом случае график приближается к осям координат при уменьшении основания. Но все так же есть общая точка (1; 0).
1. Если функция возрастающая (a > 1), при увеличении основания график приближается к осям координат.
2. Если функция убывающая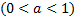 
, при уменьшении основания график приближается к осям координат.
Примеры и разбор решения заданий тренировочного модуля
№1. Найдите область определения функции: 
Решение.
Для функции 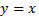область определения все положительные числа, т. е.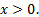 
В данной функции под логарифмом выражение, которое также должно быть больше нуля.
.
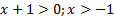Ответ: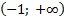 
№2 Найдите наибольшее значение функции на данном промежутке
Решение:
Рассмотрим функцию 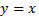. Это убывающая функция, т.к. основание меньше 1. Если функция убывает, то большему значению аргумента соответствует меньшее значение функции. Значит наибольшее значение функции будет при 
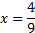, а наименьшее – при 
.
.
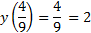Ответ: 2.