Термины и определения.
Совокупность электрических цепей с многофазными источниками питания называется многофазной системой электрических цепей.
Трехфазная цепь – частный случай многофазной цепи.
Отдельные электрические цепи, входящие в состав многофазной электрической цепи, называются фазами. Число фаз многофазной системы цепей будем обозначать через m. Термин «фаза» применяется и для обозначения аргумента синусоидально изменяющейся величины. Трех- и m -фазные системы бывают симметричные и несимметричные, уравновешенные и неуравновешенные.
Симметричной называют многофазную систему э.д.с., в которой э.д.с. в отдельных фазах равны по амплитуде и отстают по фазе друг относительно друга на углы 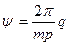 , где m =3 – число фаз, p =1 – число пар полюсов машинного генератора, q – нормирующий коэффициент, определяющий порядок чередования фаз (принимает значения q =1, 2, 3).
, где m =3 – число фаз, p =1 – число пар полюсов машинного генератора, q – нормирующий коэффициент, определяющий порядок чередования фаз (принимает значения q =1, 2, 3).
Порядок, в котором ЭДС генератора в фазных обмотках проходят через положительные максимумы, называют порядком чередования фаз (последовательностью фаз).
При q =1 получаем систему трех равных по амплитуде ЭДС, сдвинутых друг относительно друга на угол  :
:

или



Основные схемы соединения трехфазных цепей.
Существует два основных способа соединения обмоток генераторов, трансформаторов и приемников в трехфазных цепях: соединение звездой и соединение треугольником. Соединение генератора и приемника звездой показано на рис. 3.2, а соединение треугольником – на рис. 3.3.
При соединении звездой все «концы» фазных обмоток генератора и нагрузки соединяют в одну точку.
Общие точки обмоток генератора и ветвей звезды нагрузки называются нейтральными (нулевыми), а соединяющий их провод – нейтралью(нулевым проводом).
При соединении треугольником фазные обмотки генератора соединяются таким образом, чтобы «начало» одной обмотки соединялось с «концом» другой обмотки.
Общие точки каждой пары фазных обмоток генератора и ветвей приемника соединяются проводами, носящими названия линейных проводов.
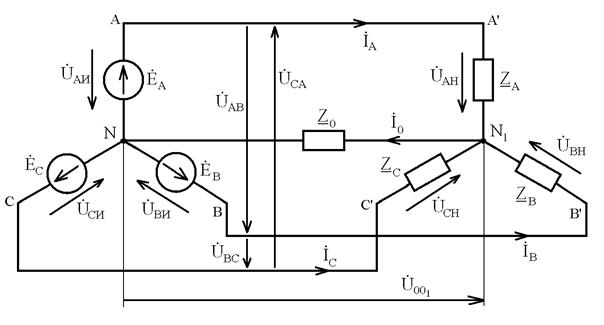
Рис. 3.2. Соединение фаз источника и нагрузки в звезду
Между линейными и фазными напряжениями и токами в симметричной трехфазной системе существуют следующие соотношения.
1) При соединении в звезду (рис. 3.2):
Iл=Iф; Uл=  Uф.
Uф.
2) При соединении в треугольник (рис. 3.3):
Uл=Uф; Iл=  Iф.
Iф.

Рис. 3.3. Соединение фаз источника и нагрузки в треугольник
Расчет трехфазных систем.
Расчет симметричных трехфазных цепей производится только для одной фазы системы, так как здесь IА=IВ=IС; Z А= Z В= Z С; jА=jВ=jС, т.е. имеет место полная симметрия. В этом случае при соединении звездой (рис. 3.2) линейные напряжения равны разностям соответствующих фазных напряжений:

а при соединении треугольником (рис. 3.3) линейные токи равны разностям соответствующих фазных токов:
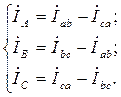
Мощность в трехфазных системах.
Активная мощность трехфазной системы определяется как сумма активных мощностей фаз нагрузки с учетом активной мощности в сопротивлении нулевого провода:
P=PA+PB+PC+P0.
Реактивная мощность трехфазной системы определяется аналогично:
Q=QA+QB+QC+Q0.
Полная мощность несимметричной трехфазной нагрузки равна
 .
.
В симметричной трехфазной системе активную, реактивную и полную мощности можно найти следующим образом:

В уравновешенных системах суммарная активная мощность постоянна и не зависит от времени: P=PA+PB+PC=3UфIфcosj=P.
В несимметричной трехфазной системе полная, активная и реактивная мощности определяется отдельно для каждой фазы нагрузки:
 A =
A = 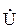 АН
АН  A = PA + jQA = UAHIA cosjA + jUAHIA sinj;
A = PA + jQA = UAHIA cosjA + jUAHIA sinj;
 B =
B = 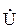 ВН
ВН  B = PB + jQB = UBHIB cosjB + jUBHIB sinj;
B = PB + jQB = UBHIB cosjB + jUBHIB sinj;
 C =
C = 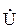 СН
СН  C = PC + jQC = UCHIC cosjC + jUCHIC sinj;
C = PC + jQC = UCHIC cosjC + jUCHIC sinj;
 0 =
0 = 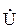 00’
00’  0 = P0 + jQ0 = U00’I0 cosj0 + jU00’I0 sinj.
0 = P0 + jQ0 = U00’I0 cosj0 + jU00’I0 sinj.