Цель работы.
Освоить методику расчёта параметров статической устойчивости автомобиля - критических углов, продольного и поперечного моментов запаса в зависимости от углов склона и расположения центра масс.
Теоретические сведения
Оценка устойчивости машин по нормальным реакциям на колёсах машины и по углу устойчивости
Рассмотрим общий случай определения нормальных реакций на колёсах машины, установленной на склоне с продольным и поперечным уклонами (рис. 1). Обозначая через α0 угол продольного наклона, а через αS, угол поперечного (бокового) наклона машины, из геометрических соотношений нетрудно установить их зависимость от угла склона α и положения машины на склоне, определяемого углом ψ:
sinα0=sinα⋅sinψ; sinαS=sinα⋅cosψ
Допустим сначала, что единственной внешней нагрузкой, действующей на машину, является сила тяжести G, приложенная в центре масс машины, в точке С с координатами l1 и hC. Силу G можно разложить на три составляющие - нормальную GN=G⋅cosα0⋅cosαS, продольную Gt=G⋅sinα0ипоперечнуюGS=G⋅cosα0⋅sinαS.
Геометрическая сумма этих сил равна, очевидно, равнодействующей силе G:
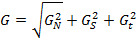
Каждая из отмеченных сил со стороны поверхности качения вызовет соответствующие реакции связей - нормальные на передних и задних колёсах RА,Б = RК1 и RВ,Г=RК2, боковые на левых и правых колёсах SА,В и SБ,Г и касательные реакции Т1 и Т2. При статическом положении машины реакции связей равны по значению и противоположно направлены соответствующим активным силам.
Не останавливаясь подробнее на методе определения опорных реакций, который в принципе ничем не отличается от определения реакций для плоской системы сил, рассмотренного нами ранее, запишем окончательные выражения для нормальных реакций поверхности качения на колесах А и Б (передних), В и Г (задних):
|
|
RA=½·G·ξA; RБ=½·G·ξБ; RВ=½·G·ξВ; RГ=½·G·ξГ;
где ξi(i = А, Б, В, Г) — коэффициенты перераспределения нормальных реакций, определяемые по формулам:
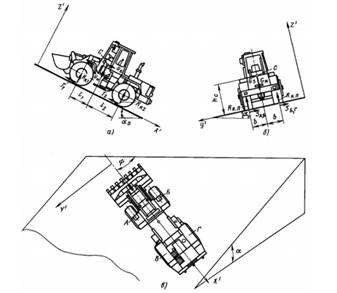
Рис. 1. Схемы для определения нормальных реакций на колёсахмашины, установленной на площадке с продольным и поперечным уклонами.
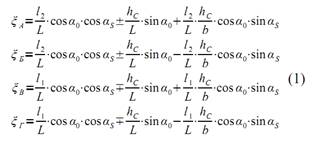
При установке машины на горизонтальной плоскости α0=αS=0 и тогда
ξA=ξБ=l2/L; ξВ=ξГ=l1/L;
Зная коэффициенты перераспределения ξi, для каждого колеса, нетрудно найти суммарные нормальные реакции на передних и задних колёсах машины RК1 и RК2 и на её левых и правых колёсах RК.Л. и RК.П.:
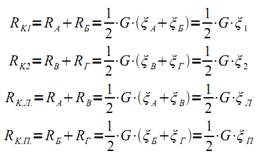
где
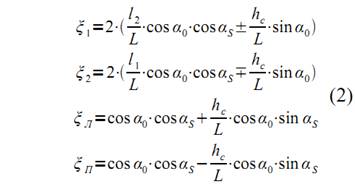
Из приведённых выражений следует, что при установке машины на горизонтальной плоскости (α0 = αS = 0)
; 
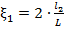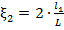; ξЛ=1; ξП=1
В выражениях (1) в (2) верхние знаки, стоящие перед вторыми членами, относятся к случаю движения машины вниз по склону или когда машина установлена так, что её передние колёса располагаются в нижней част склона, а нижние знаки относятся к случаю движения машины вверх во склону, когда её передние колёса находятся на верхней части склона (см. рис 1, а).
Очевидно, что равенство нулю нормальной реакции на внешних по отношению к оси опрокидывания опорах будет означать их полную разгрузку и потерю контакта с основанием, что, как мы уже отмечали, при статическом нагружении машины равносильно её опрокидыванию. Поэтому можно воспользоваться только что полученными выражениями для нормальных реакций на колёсах машины и из условия равенства их нулю найти условия, определяющие предельную устойчивость машины.
|
|
Так, применительно к схеме, показанной на рис.1, а, условием продольного опрокидывания является
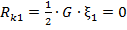, или, что то же, ξ1 = 0.
Тогда с учётом выражения (2)
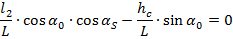
Обозначив l2=lC и разделив обе части этого уравнения наcosα0 найдём предельное значение угла наклона машины в продольной плоскости, превышениекоторого вызовет ее опрокидывание:
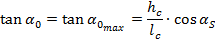
В дальнейшем угол α0МАХ мы будем обозначать через αУСТ и называть его углом продольной устойчивости машины
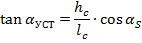
Как видим, в общем случае угол продольной устойчивости машины зависит и от угла её бокового наклона αS: чем больше боковой наклон машины, тем ниже её продольная устойчивость. При α0 = 0
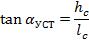
Для положения машины, показанного на рис.1, б, потеря боковой устойчивости наступит при полной разгрузке правых колёс машины, находящихся на верхней части склона, т. е. при условии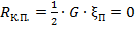 
или приξп=0. С учётом выражения (2) это условие можно записать так:
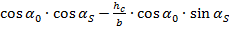=0
Обозначив в этом уравнении b = bC (поперечная координата центра масс машины) и разделив обе части уравнения на cosα0⋅cosαS получим
здесь αSУСТ - угол боковой устойчивости машины.
Если машина установлена на склоне, углы которого α0 и αS, меньше,чем углы устойчивости машины в соответствующих направлениях, то в этом случае разности между значениями углов устойчивости и фактическими углами наклона машины пределяют так называемые углы запаса устойчивости:
αзап=αуст−α0,или αSзап=αSуст−αS.
|
|
Аналогичным образом, воспользовавшись выражением, определяющим положение центра давления хД гусеничного хода, можно найти предельный угол наклона в продольной плоскости для гусеничной машины. Для этого значение хД нужно приравнять нулю (центр давления выходит за пределы опорной длины гусениц или опорного контура машины) и полученное равенство решить относительно угла α:
lc−hc⋅tanα=0
откуда
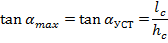
Разумеется, что положения машины, при которых углы её наклона достигают критических значений, равных αУСТ, являются в определенном смысле теоретическими, и машина поэтому должна всегда иметь определенный запас устойчивости. Так, для гусеничных машин можно считать, что предельное положение центра давления, при котором машина ещё сохраняет продольную устойчивость и может работать, соответствует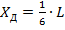 
, где L - опорная длина гусениц. В этом случае
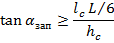
Из-за неравномерного распределения нормальных нагрузок на передние и задние, либо на правые и левые опоры машины или из-за неодинакового давлениявоздуха в шинах машина получает дополнительный наклон (крен) на угол αП, обусловленный деформацией её опор и основания (грунта):
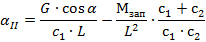
где МЗАП - момент запаса продольной ила боковой устойчивости машины: с1 и с2 - соответственно суммарные приведённые жёсткости основания и опор машины, находящихся со стороны оси опрокидывания, и опор машины, внешних по отношению к оси опрокидывания; L - база ходовой части машины (при определении продольного крена) – либо колея ходовой части (при определении поперечного крена).
При α = 0, с1=с2=с и среднем расположении центра масс машины (Мзап=Муст=(G⋅L)/2) угол крена αII=0. С учётом крена машины
αзад=αуст−α−αII