Минимизация логических функций

Недостаток методов получения функций СНДФ или СНКФ, обеспечивающего, в общем, правильное функционирование устройств, состоит в том, полученные схемы чаще всего неоправданно сложные. Они требуют большого числа логических элементов, имеют низкую экономичность. Во многих случаях удается упростить логическое выражение, не изменив функции. Методы упрощения функции называются методами мимнимизации функций.
Минимизация означает переход от СДНФ к ДНФ с минимумом слагаемых (избавиться от "совершенства"), при этом количество множителей в каждом слагаемом должно быть также минимальным, то есть максимально уменьшить количество переменных и операций в СДНФ.
Для минимизации логических функций возможно использовать разные методы:
· карта Карно (Вейча)
· Квайна
· Квайна- Мак-Класки
· Петрика
Отличие метода карт Карно от карт Вейча заключается в способе обозначения строк и столбцов карт. У карт Карно строки и столбцы обозначаются с помощью кода Грея. Однако, принципиальной разницы между ними нет.
Метод минимизационных карт Карно (или карт Вейча) хорошо работает при числе аргументов 3,4 и даже 5 и обеспечивает простоту получения результата. Этот метод основан на зрительном анализе таблиц (карт) и не может быть применен для обработки вычислительной техникой.
Карта Карно строится в соответствии с таблицей истинности логической функции. Столбцы и строки карты Карно обозначаются прямыми и инверсными переменными данной функции.
Рис 4.3.1. Карта Карно для 2-х и для 3-х переменных 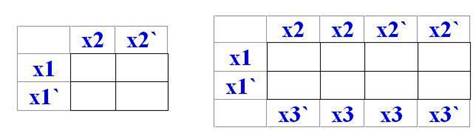
Число клеток карты равно числу всех возможных комбинаций входных переменных, т.е. 2ⁿ, где n - чило входных переменных. Это также значит, что число клеток карты равно максимальному числу минтерм СНДФ.
Каждая клетка карты соответствует логическому произведению (прямого или инверсного значения) переменных, на пересечении которых она находится, что соответствует минтерме СНДФ. В карту Карно заносятся соответствующие значения минтерм.
Строки и столбцы карты обозначаются таким образом, чтобы любые соседние клетки по строкам или по столбцам отличались бы между собой значением только одной переменной. Такое обозначение соответствует последовательности чисел в коде Грея. Это сделано для того, чтобы было бы возможно применить закон склеивания.
Клетки, находящиеся на границах одной строки или столбца, так же считаются соседними.
Рис. 4.3.2. Карта Карно строится на основании таблицы истинности
| a | b | c | f |
| а`b`c` | |||
| ab`c` | |||
| a`bc` | |||
| a`b`c | |||
| abc` | |||
| ab`c | |||
| a`bc | |||
| abc |
Каждая клетка карты соответствует произведению переменных, на пересечении которых она находится.
Рис. 4.3.3. Принцип составления карты Карно
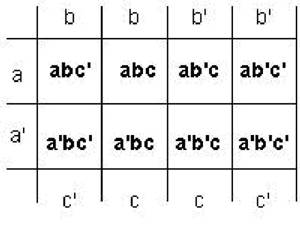
Для минимизации функций используется закон «склеивания»:
ab + ab` = a
Если переменная (аргумент) изменяет свое значение, а функция при этом остается неизменной, то эту переменную можно исключить из выражения.
Правило минимизации.
Для получения минимальной функции НДФ (или МНДФ) охватывают областями все клетки, имеющие значение 1 и являющиеся соседними. Эти области должны быть прямоугольной формы и содержать чётное количество клеток. Для каждой области записывается неизменяющаяся часть объедененных минтерм. При этом минимизируемые области могут иметь общие минтермы (пересекаться). В заключение все минтермы суммируются.
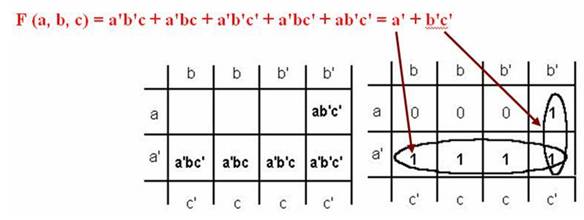
Рис. 4.3.4. Пример минимизации трех переменных с помощью карты Карно
В данном примере, произведения, образующие квадрат (с учётом замкнутости краевых линий диаграммы), позволяют исключить из общего выражения две переменные. При этом количество минтерм также сократилось.
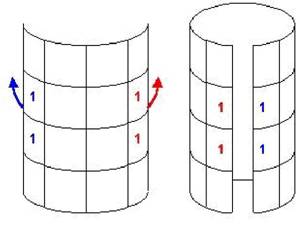
Рис. 4.3.5. Метод скручивания карты Карно
Крайние квадраты карты являются соседними при ее скручивании. Это значит, что они тоже подлежат минимизации. На плоскости можно изобразить карту Карно для 4-х переменных. Для 5 и более переменных необходимы объемные фигуры.
 Пример
Пример
Допустим, что задана логическая функция с помощью таблицы истинности.
Рис. 4.3.6. Пример создания логической функции
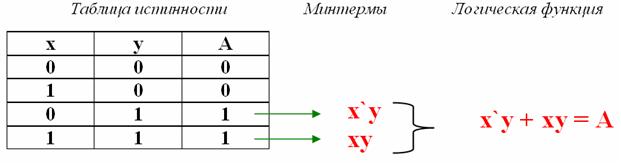
Составим карту Карно, объеденим единицы и получим минимальную форму функции.
Рис. 4.3.7. Пример минимизации
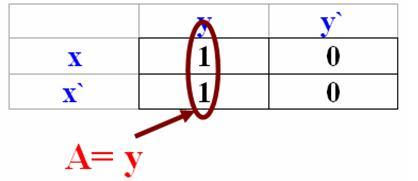
Переменная х изменяется, и поэтому её можно упустить!
Минимизировать нижеприведённые функции, представленные картами Карно.
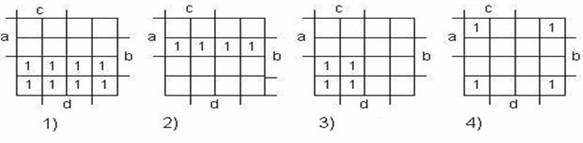
Не заполненные клетки соответствуют нулю. Переменные, обозначенные буквами, соответствуют прямому значению, а не обозначенные - инверсному.
Правильные решения для приведенных примеров:
1) F = a` 2) F = ab 3) F = a`c 4) F = b`d`
Задание 1
Минимизировать функцию, представленную картой Карно.
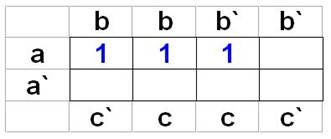
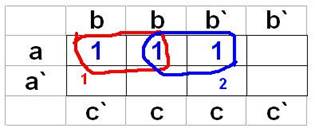
F = (1) + (2) = ab + ac
Задание 2
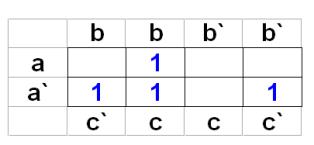
Минимизировать функцию, представленную картой Карно.
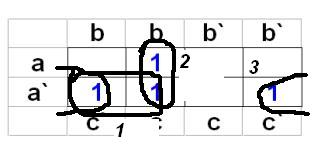 F = (1) + (2) + (3) = a`b + bc + a`c`
F = (1) + (2) + (3) = a`b + bc + a`c`
Задание 3
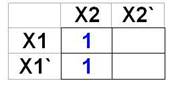
Для заданной таблицы истинности составить CНДФ, карту Карно и минимизировать функцию.
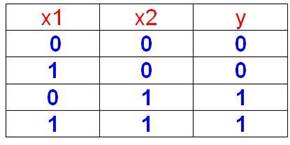
F = x2
Задание 4
Для заданной таблицы истинности составить CНДФ, карту Карно и минимизировать функцию.
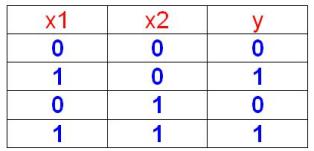
F = x1x2`+ x1x2 = x1
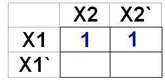
Задание 5
Для заданной таблицы истинности составитьCНДФ, карту Карно и минимизировать функцию.
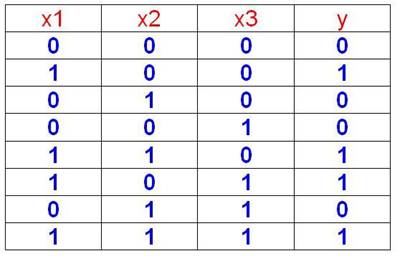
F = x1x2`x3` + x1x2x3` + x1x2`x3 + x1x2x3
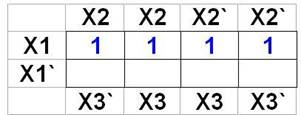
F = x1
Задание 6
Для заданной таблицы истинности составить CНДФ, карту Карно и минимизировать функцию.
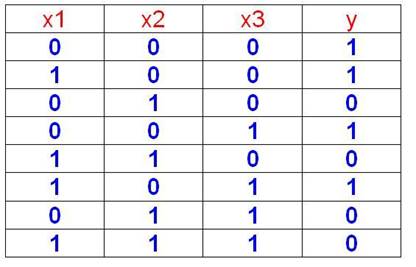
F = x1`x2`x3` + x1x2`x3` + x1`x2`x3 + x1x2`x3
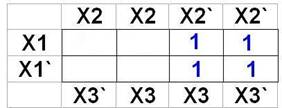
F = x2`
 МНКФ
МНКФ
По картам Карно также возможно получить Минимальную Нормальную Коньюктивную Форму логической функции. Для этого объеденяют не единицы, а нули. Из выражения минтерм также исключают изменяющиеся переменные. Однако в результирующей функции переменные записываются в инвертном виде. При этом минтермы являются логической суммой входных переменных, а функция есть конъюнкция входящих в нее минтерм.
Рис. 4.3.8. Пример получения МНКФ
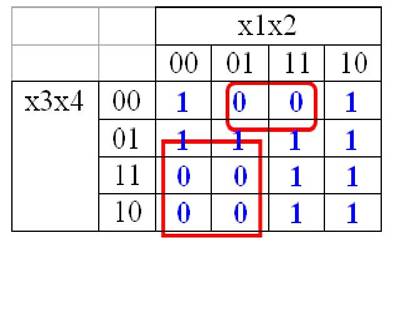
F = (x2` + x3 + x4) · (x1 + x3`)
представлять функции в ДНФ или КНФ с минимальным числом членов и минимальным числом букв в членах.
Этот метод содержит два этапа преобразования выражения функции: на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращенной форме, на втором этапе - переход от сокращенной формы логического выражения к минимальной форме.
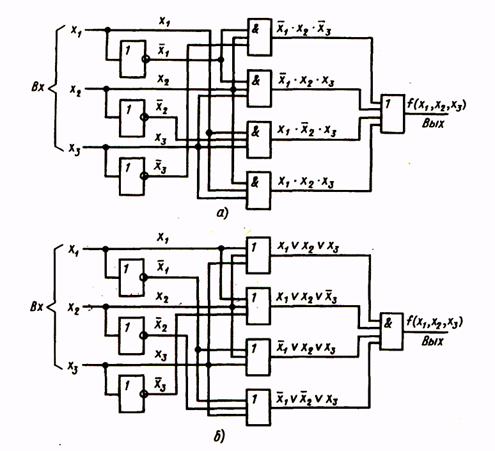
Рис. 1
Первый этап (получение сокращенной формы). Пусть заданная функция представлена в СДНФ. Переход к сокращенной форме основан на последовательном применении двух операций: операции склеивания и операции поглощения.
Для выполнения операции склеивания в выражении функции выявляются пары членов вида 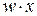 и
и 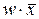 , различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом - с инверсией. Затем проводится склеивание таких пар членов:
, различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом - с инверсией. Затем проводится склеивание таких пар членов: 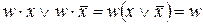 , и результаты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее выполняется операция поглощения. Она основана на равенстве
, и результаты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее выполняется операция поглощения. Она основана на равенстве 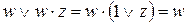 (член w поглощает член
(член w поглощает член 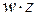 ). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции склеивания.
). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции склеивания.
Операции склеивания и поглощения выполняются последовательно до тех пор, пока это возможно. Покажем этот этап минимизации логического выражения на примере построения логического устройства для функции, заданной в табл. 2.
Таблица 2

Совершенная ДНФ этой функции
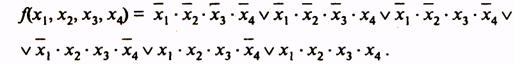 (3)
(3)
Для получения сокращенной формы проводим операции склеивания и поглощения:
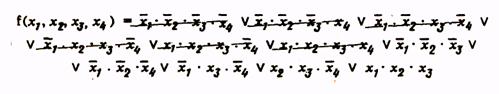 (4)
(4)
Второй этап (получение минимальной формы). Выражение (4) представляет собой сокращенную форму логического выражения заданной функции, а члены его являются простыми импликантами функции. Переход от сокращенной формы к минимальной осуществляется с помощью импликантной матрицы, приведенной в табл. 3.
Таблица 3
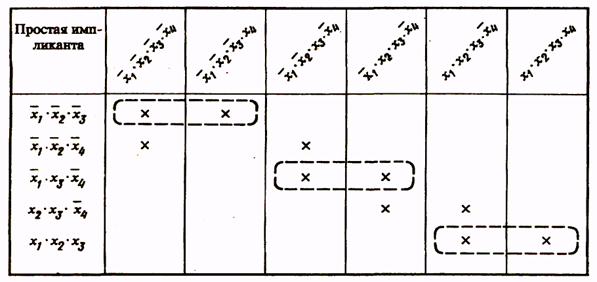
В столбцы импликантной матрицы вписываются члены СДНФ заданной функции, в строки - простые импликанты функции, т.е. члены сокращенной формы логического выражения функции. Отмечаются (например, крестиками) столбцы членов СДНФ, поглощаемых отдельными простыми импликантами. В табл. 3 простая импликанта 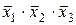 поглощает члены
поглощает члены 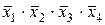 ,
, 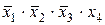 (в первом и во втором столбцах первой строки поставлены крестики).
(в первом и во втором столбцах первой строки поставлены крестики).
Вторая импликанта поглощает 1-й и 3-й члены СДНФ (крестики поставлены в первом и третьем столбцах второй строки) и т.д. Импликанты, которые не могут быть лишними и, следовательно, не могут быть исключены из сокращенной формы, составляют ядро. Входящие в ядро импликанты легко определяются по импликантной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только данной импликантой.
В рассматриваемом примере ядро составляют импликанты 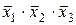 и
и 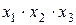 (только ими перекрываются второй и шестой столбцы матрицы). Исключение из сокращенной формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую уже в нелишний член.
(только ими перекрываются второй и шестой столбцы матрицы). Исключение из сокращенной формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую уже в нелишний член.
Для получения минимальной формы достаточно выбрать из импликант, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждой из этих импликант, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвертый столбцы матрицы. Это может быть достигнуто различными способами, но, так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать импликанту 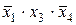 .
.
Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции
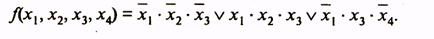 (5)
(5)
Структурная схема, соответствующая этому выражению, приведена на рис.2.
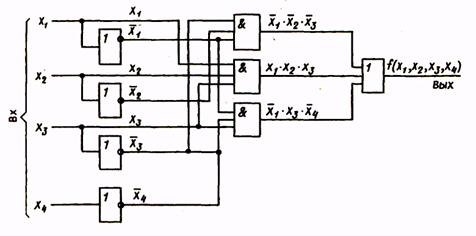
Рис. 2
До сих пор рассматривалось получение минимальной ДНФ. При использовании метода Квайна для получения минимальной конъюнктивной нормальной формы (МКНФ) логической функции имеются следующие особенности:
- исходной для минимизации формой логического выражения заданной функции является СКНФ;
- пары склеиваемых членов имеют вид w v д: и wv x;
- операция поглощения проводится в соответствии с выражением
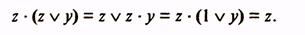
Рассмотрим применение метода Квайна на примере минимизации функции, заданной таблицей истинности (табл. 4).
Таблица 4

Совершенная КНФ рассматриваемой функции
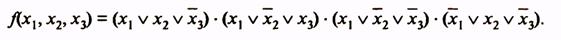
Склеивающиеся пары членов:
1-й и 3-й члены (результат склеивания 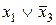 );
);
1-й и 4-й члены (результат склеивания 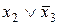 );
);
2-й и 3-й члены (результат склеивания 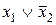 ).
).
Проводим операции склеивания и поглощения:
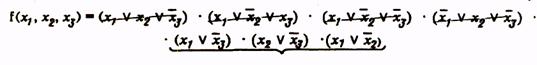
Члены операции склеивания
Полученное выражение является сокращенной формой функции.
Для перехода к минимальной форме строим импликантную матрицу (табл. 5).
Таблица 5
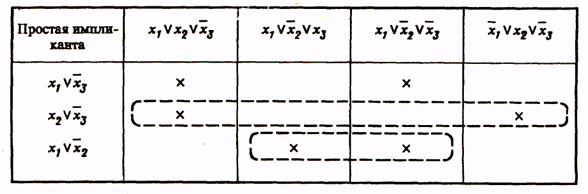
Все столбцы матрицы перекрываются импликантами 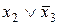 и
и 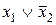 . Следовательно, член
. Следовательно, член 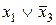 является лишним и минимальная конъюнктивная нормальная форма (МКНФ) заданной функции
является лишним и минимальная конъюнктивная нормальная форма (МКНФ) заданной функции
загрузка...
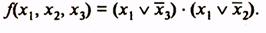
1.3. Минимизация логических функций методом карт Вейча
Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результатов. Он используется при минимизации относительно несложных функций (с числом аргументов до пяти). Карта Вейча представляет собой определенную форму таблицы истинности. Табл. 6 являются картами Вейча для функций соответственно двух (а), трех (б), четырех (в) аргументов.
Таблица 6
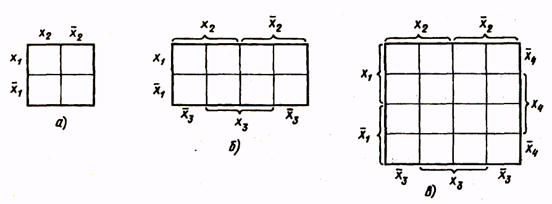
Каждая клетка карты соответствует некоторому набору значений аргументов. Этот набор аргументов определяется присвоением значения лог.1 буквам, на пересечении строк и столбцов которых расположена клетка. Так, в карте функций четырех аргументов (табл. 6в) клетки первой строки соответствуют следующим комбинациям значений аргументов:
1-я клетка 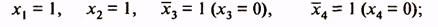
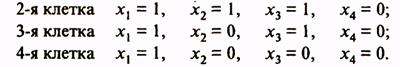
Число клеток карты равно числу всех возможных наборов значений аргументов 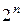 (п — число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности (табл. 7). Таблица истинности этой функции в форме карты Вейча представлена табл. 8.
(п — число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности (табл. 7). Таблица истинности этой функции в форме карты Вейча представлена табл. 8.
Таблица 7

Карта Вейча определяет значения функции на всех возможных наборах значений аргументов и является таблицей истинности. Карты Вейча компактны, но главное их достоинство состоит в следующем. При любом переходе из одной клетки в соседнюю вдоль столбца или строки изменяется значение лишь одного аргумента функции. Следовательно, если в паре соседних клеток содержится 1, то над соответствующими им членами канонической формы может быть проведена операция склеивания. Таким образом, облегчается поиск склеиваемых членов.
Таблица 8Таблица 9
Сформулируем правила получения МДНФ функций с помощью карт Вейча. Все клетки, содержащие 1, объединяются в замкнутые области. При этом каждая область должна представлять собой прямоугольник с числом клеток 2k, где k - 0, 1, 2,.... Значит, допустимое число клеток в области 1, 2, 4, 8,...,. Области могут пересекаться и одни и те же клетки могут входить в разные области. Затем проводится запись выражения МДНФ функции. Каждая из областей в МДНФ представляется членом, число букв в котором на k меньше общего числа аргументов функции п (т.е. равно 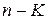 ). Каждый член МДНФ составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (без инверсии либо с инверсией).
). Каждый член МДНФ составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (без инверсии либо с инверсией).
Таким образом, при охвате клеток замкнутыми областями следует стремиться, чтобы число областей было минимальным (при этом минимальным будет число членов в МДНФ функции), а каждая область содержала возможно большее число клеток (при этом минимальным будет число букв в членах МДНФ функции).
Рассмотрим минимизацию с помощью карты Вейча функции трех аргументов, представленной табл. 9. Все клетки, содержащие 1, охватываются двумя областями. В каждой из областей 21 клеток, для них n-k = 3-l = 2, и эти области в МДНФ будут представлены членами, содержащими по две буквы. Первой области соответствует член 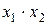 (аргумент
(аргумент 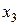 здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член
здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член 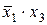 . Следовательно, МДНФ функции
. Следовательно, МДНФ функции
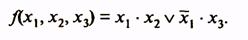
Рассмотрим пример минимизации функции четырех аргументов, заданной табл. 10. Первая и четвертая области имеют по две клетки, для них п- k - 4 -1=3. Эти области в МДНФ будут представлены членами, содержащими по три буквы. Вторая и третья области содержат по четыре клетки и в МДНФ выражаются членами, содержащими по две буквы (п - k = 4 -2 = 2). Минимальная ДНФ функции
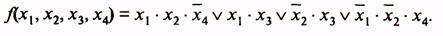
Таблица 10Таблица 11
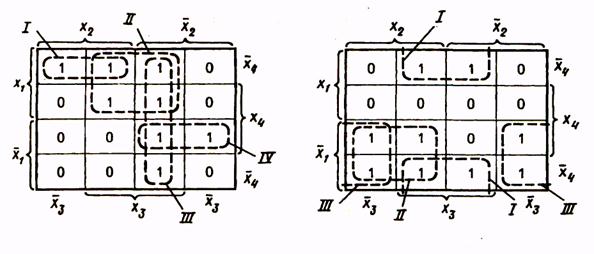
При построении замкнутых областей допускается сворачивание карты в цилиндр с объединением ее противоположных граней. В силу этого крайние клетки строки или столбца таблицы рассматриваются как соседние и могут быть объединены в общую область. Иллюстрацию этого приема проведем на примере функции, представленной табл. 11. Минимальная ДНФ функции
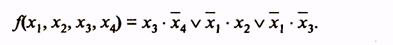
В силу допустимости такого сворачивания карты вдоль горизонтальной и вертикальной осей, например: клетки, расположенные в четырех углах карты функции четырех переменных, оказываются соседними и могут быть объединены в одну область. Покажем это на примере минимизации функции, заданной табл. 12. Минимальная ДНФ функции
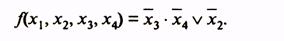
Таблица 12Таблица 13
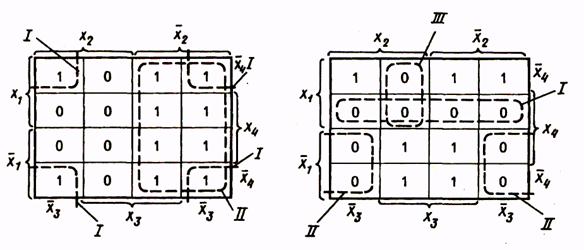
Для получения МКНФ функции замкнутыми областями охватываются клетки с нулевыми значениями функции, и при записи членов логического выражения берутся инверсии аргументов, на пересечении которых находятся области. Так, для функции, приведенной в табл. 13, МКНФ
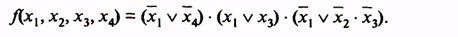
До сих пор рассматривались логические функции с числом аргументов до четырех. Представление функции и минимизация ее с помощью карт Вейча усложняются, если число аргументов больше четырех. В табл. 14 показано представление с помощью карт Вейча функции пяти аргументов.
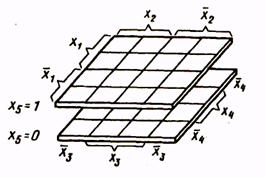 Рис.3 Рис.3
| Таблица истинности здесь состоит из двух карт, каждая из которых представляет собой карту четырех переменных. Одна из них соответствует х5= 1, другая - х5 = 0. Эти карты можно мысленно расположить одна над другой (рис.3). При этом области охвата клеток могут быть трехмерными, т.е. одной областью могут охватываться клетки двух карт. |
Для функции, приведенной в табл. 23, МДНФ
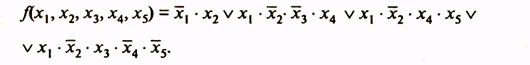
Таблица 14
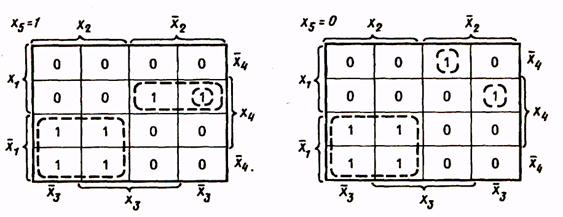
Для минимизации функции с числом аргументов, большим пяти, карты Вейча оказываются неудобными. Минимизация таких функций может быть выполнена методом Квайна.
1.4. Минимизация функций с использованием карт Карно
Отличие карт Карно от карт Вейча заключается в способе обозначения строк и столбцов таблицы истинности. Таблица 15 иллюстрирует карты Карно для функций трех и четырех аргументов.
Аргументы функции делятся на две группы, комбинации значений аргументов одной группы приписываются столбцам таблицы, комбинации значений аргументов другой группы - строкам таблицы. Столбцы и строки обозначаются комбинациями, соответствующими последовательности чисел в коде Грея (это сделано для того, чтобы склеивающиеся клетки находились рядом). Обозначения столбца и строки, на пересечении которых находится клетка таблицы, образуют набор, значение функции на этом наборе записывается в клетку.
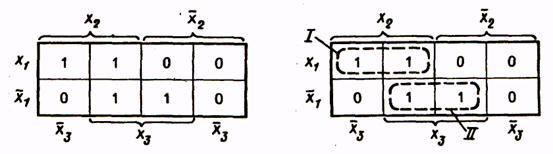
Для получения МДНФ функции охватываются областями клетки таблицы, содержащие 1. Как и в случае минимизации с помощью карт Вейча, области должны быть прямоугольной формы и содержать 2k клеток (при целочисленном значении k). Для каждой области составляется набор из двух комбинаций: приписанных столбцам и приписанных строкам, на пересечении которых расположена область. При этом если области соответствуют несколько комбинаций кода Грея, приписанных столбцам или строкам, то при составлении набора области записывается общая часть этих комбинаций, а на месте различающихся разрядов комбинаций ставятся звездочки. Например, для функции, представленной табл. 16, области I будет соответствовать набор 1*00 или член МДНФ 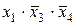 , области II - набор 0**1 или член МДНФ
, области II - набор 0**1 или член МДНФ 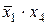 . Таким образом, для этой функции МДНФ
. Таким образом, для этой функции МДНФ
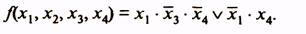
Таблица 15
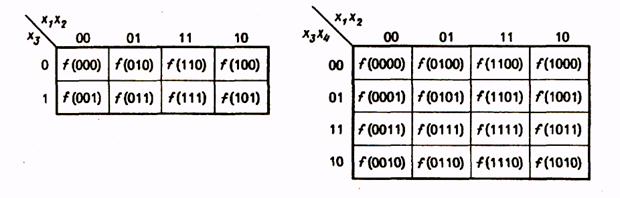
Таблица 16Таблица 17
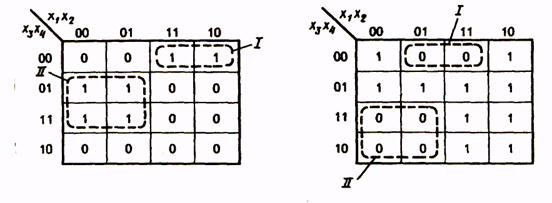
Для получения МКНФ областями охватываются клетки, содержащие 0, и члены МКНФ записываются через инверсии цифр, получаемых для наборов отдельных областей. Так, для функции, представленной в табл. 17, области I соответствует набор *100 и член МКНФ 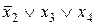 , области II — набор О*1* и член
, области II — набор О*1* и член 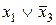 . Таким образом, МКНФ функции
. Таким образом, МКНФ функции
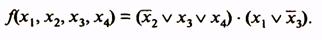
1.5. Задание для выполнения
Для функции четырех аргументов F(x1,x2,x2,x4):
а) записать СДНФ;
б) записать СКНФ;
в) упростить функцию с помощью метода Квайна – записать МДНФ и МКНФ;
г) упростить функцию с помощью карты Вейча – записать МДНФ и МКНФ;
д) упростить функцию с помощью карты Карно – записать МДНФ и МКНФ;
е) сравнить МДНФ и МКНФ, полученные в п. в)-д);
ж) реализовать МДНФ и МКНФ на логических элементах.
Минимизации логических функций. Метод Квайна
Пусть логическая функция 𝑓(𝑥4, 𝑥3, 𝑥2, 𝑥1) задана в виде f (2,5,6,7,10,12,13,14)=1. В скобках заданы номера наборов четырех переменных, на которых логическая функция принимает единичное значение.
Заменим эти номера (десятичные числа) их двоичным представлением, получаем наборы переменных (𝑥4, 𝑥3, 𝑥2, 𝑥1), на которых логическая функция принимает единичное значение:
f (0010,0101, 0110, 0111, 1010, 1100, 1101, 1110) =1. Эту логическую функцию можно представить в совершенной дизъюнктивной нормальной форме (символ конъюнкции для краткости опущен):
𝑓 = 𝑥̅4𝑥̅3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥̅2𝑥1 ∨ 𝑥̅4𝑥3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥2𝑥1 ∨ 𝑥4𝑥̅3𝑥2𝑥̅1 ∨ 𝑥4𝑥3𝑥̅2𝑥̅1 ∨ 𝑥4𝑥3𝑥̅2𝑥1 ∨ 𝑥4𝑥3𝑥2𝑥̅1
Но, оказывается, есть более экономное представление, а именно 2 1 4 3 1 4 3 2 f = x x Ú x x x Ú x x x Процедура получение такого представления называется минимизацией функции, а полученная форма минимальной нормальной формой. Рассмотрим один из методов такой минимизации, который называется методом Квайна. Данный метод делится на три этапа. 1. На первом этапе минимизации исходную СДНФ упрощаем, используя закон склеивания, AB+ ĀB=B (A+ Ā)=B. Применяя несколько раз закон склеивания к СДНФ функции f получим: 𝑥̅4𝑥̅3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥̅2𝑥1 ∨ 𝑥̅4𝑥3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥2𝑥1 ∨ 𝑥4𝑥̅3𝑥2𝑥̅1 ∨ 𝑥4𝑥3𝑥̅2𝑥̅1 ∨ 𝑥4𝑥3𝑥̅2𝑥1 ∨ 𝑥4𝑥3𝑥2𝑥̅1 𝑥̅3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥̅2𝑥1 ∨ 𝑥̅4𝑥3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥2𝑥1 ∨ 𝑥4𝑥3𝑥̅2𝑥̅1 ∨ 𝑥4𝑥3𝑥̅2𝑥1 ∨ 𝑥4𝑥3𝑥2𝑥̅1 𝑥̅3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥̅2𝑥1 ∨ 𝑥3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥2𝑥1 ∨ 𝑥4𝑥3𝑥̅2𝑥̅1 ∨ 𝑥4𝑥3𝑥̅2𝑥1 𝑥̅3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥̅2𝑥1 ∨ 𝑥3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥2𝑥1 ∨ 𝑥4𝑥3𝑥̅2 𝑥̅3𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥1 ∨ 𝑥3𝑥2𝑥̅1 ∨ 𝑥4𝑥3𝑥̅2 𝑥2𝑥̅1 ∨ 𝑥̅4𝑥3𝑥1 ∨ 𝑥4𝑥3𝑥̅2 Удачная последовательность склеиваний привела к минимальной форме. Однако, мы могли бы привести формулу к выражению: 2 1 4 3 1 1 3 2 3 2 1 4 3 2 4 3 1 f = x x Ú x x x Ú x x x Ú x x x Ú x x x Ú x x x. Теперь задача состоит в том, чтобы убрать лишние ∨−слагаемые в данном представлении так, чтобы ∨ − сумма оставшихся членов также представляла нашу функцию. 2. На втором этапе, составляем таблицу Куайна для функции f 𝑥4, 𝑥3, 𝑥2, 𝑥1 0010 0101 0110 0111 1010 1100 1101 1110 Х Х 1 0 1 0 1 0 1 0 0 1 0 1 Х 1 0 1 0 1 0 0 0 0 0 1 1 X 0 0 1 1 0 0 0 0 X 1 0 1 0 1 0 0 0 0 1 0 1 1 0 X 0 0 0 0 0 1 1 0 1 1 X 0 0 0 0 0 0 1 0 1 В этой таблице в первом столбце перечислены все, полученные на первом этапе упрощения, слагаемые в символической записи, а в первой строке – наборы значений переменных (𝑥4, 𝑥3, 𝑥2, 𝑥1), на которых логическая функция принимает единичное значение. Красные единицы и нули строки соответствуют значениям, которые принимает функция первого столбца, на соответствующем синем наборе значений переменных (символическая запись позволяет процесс вычисления заменить визуальным эффектом – «накрытием», 0 накрывает 0, 1 накрывает 1, а Х накрывает 0 и 1). 3. Наконец, на третьем этапе выбираем наименьшее число ∨− слагаемых (строк) так, чтобы «накрыть» всю первую строку. Объединение красных единиц выбранных строк, должны накрывать всю первую строку. В результате, получаем: 2 1 4 3 1 4 3 2 f = x x Ú x x x Ú x x x. Использованная литератураМинимизация булевых функций
Ясно, что при разработке логических схем, немаловажной является задача минимизации количества используемых элементов (другими словами, логических операций).
В связи с этим, возникает задача минимизации логических функций в некотором классе формул. В частности, в классах ДНФ и КНФ.
Минимальная ДНФ
Такая ДНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.
Минимальная КНФ
Такая КНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей КНФ.
Процесс нахождения минимальных форм, собственно, и называется минимизацией. В простых случаях, для минимизации достаточно тождественных преобразований. В более сложных – используются специальные алгоритмы.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя членами, содержащими одинаковые переменные, вхождения которых (с отрицанием и без) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
x1¯¯¯¯¯x2x3x4∨x1¯¯¯¯¯x2x3¯¯¯¯¯x4=x1¯¯¯¯¯x2x4(x3∨x3¯¯¯¯¯)=x1¯¯¯¯¯x2x4&1=x1¯¯¯¯¯x2x4.x1¯x2x3x4∨x1¯x2x3¯x4=x1¯x2x4(x3∨x3¯)=x1¯x2x4&1=x1¯x2x4.
Аналогично для КНФ:
(x1¯¯¯¯¯∨x2∨x3∨x4)(x1¯¯¯¯¯∨x2∨x3¯¯¯¯¯∨x4)=x1¯¯¯¯¯∨x2∨x4∨x3x3¯¯¯¯¯=x1¯¯¯¯¯∨x2∨x4∨0=x1¯¯¯¯¯∨x2∨x4.(x1¯∨x2∨x3∨x4)(x1¯∨x2∨x3¯∨x4)=x1¯∨x2∨x4∨x3x3¯=x1¯∨x2∨x4∨0=x1¯∨x2∨x4.
Возможность поглощения следует из очевидных равенств
A∨A¯¯¯¯=1A∨A¯=1
AA¯¯¯¯=0.AA¯=0.
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск членов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.
Минимизирующие карты Карно
Карта Карно
Графический способ минимизации булевых функций. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как построенная соответствующим образом таблица истинности функции.
Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Булевы функции NN переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе 2N2Nразличных элементарных членов.
Элементарные члены СДНФ или СКНФ образуют структуру, топологически эквивалентную NN-мерному кубу. Действительно, если рассматривать набор значений функции x1,…,xNx1,…,xN как NN-мерный вектор {x1,…,xN}{x1,…,xN}, мы получим набор точек, лежащих на ортах NN-мерной системы координат, и удаленных друг от друга на 11. Другими словами, мы получим NN-мерный гиперкуб с ребром 11.
Например, для функции двух переменных, заданной таблицей истинности:
| x1x1 | x2x2 | f(x1,x2)f(x1,x2) |
можно построить эквивалентный ей квадрат:
Или, если обозначить вершины соответствующими элементарными конъюнкциями и выделить вершины, конъюнкции которых входят в СДНФ:
0x̅₁x₂1x₁x₂0x̅₁x̅₂1x₁x̅₂
Или СКНФ:
0x₁∨x̅₂1x̅₁∨x̅₂0x₁∨x₂1x̅₁∨x₂
Можно заметить, что члены, находящиеся на одной стороне квадрата, могут быть склеены. Соответственно, если составляется ДНФ, то операции производятся только над вершинами, в которых функция имеет значение 11 (по правилам построения СДНФ). Если же составляется КНФ, то над вершинами, в которых функция имеет значение 00 (по правилам построения СКНФ).
При этом, сохраняются переменные, значение которых на стороне постоянно.
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
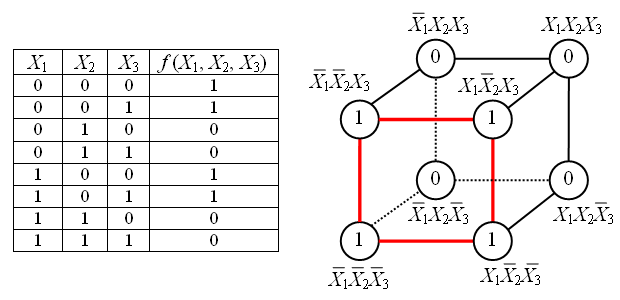
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации. Например, четыре члена, принадлежащие одной грани куба, объединяются в один с поглощением двух переменных:
x1¯¯¯¯¯x2¯¯¯¯¯x3¯¯¯¯¯∨x1x2¯¯¯¯¯x3¯¯¯¯¯∨x1¯¯¯¯¯x2¯¯¯¯¯x3∨x1x2¯¯¯¯¯x3=x1¯x2¯x3¯∨x1x2¯x3¯∨x1¯x2¯x3∨x1x2¯x3=
=x2¯¯¯¯¯(x1¯¯¯¯¯x3¯¯¯¯¯∨x1¯¯¯¯¯x3∨x1x3¯¯¯¯¯∨x1x3)=x2¯¯¯¯¯(x1¯¯¯¯¯∨x1)(x3¯¯¯¯¯∨x3)=x2¯¯¯¯¯=x2¯(x1¯x3¯∨x1¯x3∨x1x3¯∨x1x3)=x2¯(x1¯∨x1)(x3¯∨x3)=x2¯
В общем случае можно сказать, что 2K2K членов, принадлежащие одной KK–мерной грани гиперкуба, склеиваются в один член, при этом поглощаются KKпеременных.
Карта Карно представляет собой развертку гиперкуба на плоскость. Например, трехмерный куб из предыдущего примера можно развернуть следующим образом:
1x̅₁x̅₂x̅₃1x̅₁x̅₂x₃0x̅₁x₂x̅₃0x̅₁x₂x₃0x₁x₂x₃0x₁x₂x̅₃1x₁x̅₂x₃1x₁x̅₂x̅₃
Карта Карно является представлением такой двумерной развертки в виде таблицы.
| x3∖x1x2x3∖x1x2 | ||||
В этой карте самые левые ячейки смежны самым правым.
Ясно, что на одной KK-мерной грани могут лежать 2K2Kвершин. Следовательно, в карте Карно выбираются группы по 2K2K смежных ячеек, и в результирующую ДНФ или КНФ входят только те переменные, которые неизменны в рамках данной группы. Общее число членов соответствует числу групп в карте Карно, а число неизменных переменных обратным образом зависит от количества элементов в группе. Как следствие, группы необходимо выбирать как можно более большими. Следует отметить, что одна комбинация переменных может входить в несколько групп.
Для функций четырех переменных, требуется развертка 4-мерного гиперкуба. Карта Карно в таком случае имеет вид:
| x3x4∖x1x2x3x4∖x1x2 | ||||
| f(0,0,0,0)f(0,0,0,0) | f(0,1,0,0)f(0,1,0,0) | f(1,1,0,0)f(1,1,0,0) | f(1,0,0,0)f(1,0,0,0) | |
| f(0,0,0,1)f(0,0,0,1) | f(0,1,0,1)f(0,1,0,1) | f(1,1,0,1)f(1,1,0,1) | f(1,0,0,1)f(1,0,0,1) | |
| f(0,0,1,1)f(0,0,1,1) | f(0,1,1,1)f(0,1,1,1) | f(1,1,1,1)f(1,1,1,1) | f(1,0,1,1)f(1,0,1,1) | |
| f(0,0,1,0)f(0,0,1,0) | f(0,1,1,0)f(0,1,1,0) | f(1,1,1,0)f(1,1,1,0) | f(1,0,1,0)f(1,0,1,0) |
В данном случае, все крайние ячейки смежны друг другу. Это можно себе представить, натянув эту развертку на тор (“бублик”):
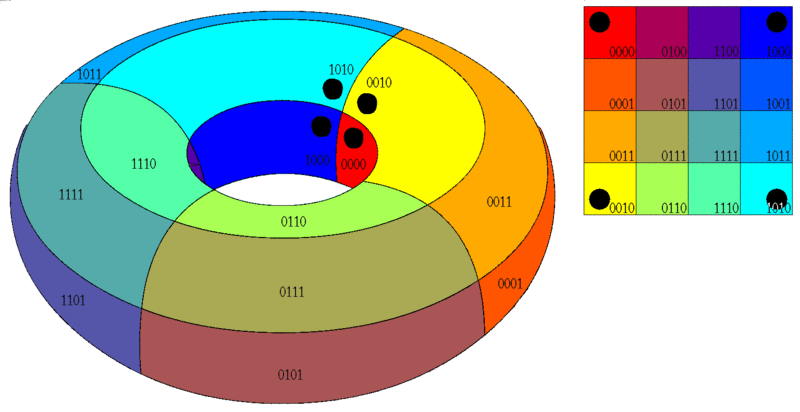
Возможно так же построение карт Карно для функций 5 и 6 переменных, однако работа с ними значительно затрудена. Для числа переменных, большего 6, использование карт Карно попросту непрактично.
Пример
Рассмотрим функцию, имеющую следующую таблицу истинности:
| x1x1 | x2x2 | x3x3 | x4x4 | f(x1,x2,x3,x4)f(x1,x2,x3,x4) |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2021-01-30 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд