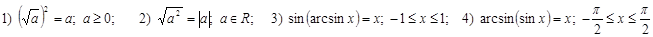РАЗДЕЛ 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Тема 3.1. Функция одной переменной
Лекция 1. Функция. Способы задания. Свойства
1.1. Функция
Определение. Закон, который каждой точке x из некоторого множества X ставит в соответствие определенное число y из множества Y, называется функцией.
Обозначение: y = f(x) или x —f—> y, где f – это закон.
Множество X – область определения функции (ООФ): D(y) или D(f), где переменная х – аргумент функции;
Множество Y – множество значений функции (МЗФ): E(y) или E(f)
Функция может быть: одной переменной y = f(x), двух переменных z = f(x,y) и более.
1.2. Способы задания функции
1) Аналитический, т.е. формулой. Например: y = 2x – 5, f(x) = (2x2 – 3)3, f(x) = x n, f(x) = sin x...
2) Табличный.
3) Графический.
Определение. а) Графиком функции y = f(x) называется множество точек плоскости с координатами (x, f(x)), где xÎ D(f), (для функции одной переменной)
б) Графиком функции z = f(x,y) называется множество точек пространства с координатами
(x, y, f(x, y)), где (x, y)Î D(f), (для функции двух переменных).
Из графика одной функции путем преобразования графика можно получить бесконечно много графиков других функций.
Простейшие преобразования графиков
·  сдвиг графика вверх по оси Y
сдвиг графика вверх по оси Y
·  сдвиг графика вниз по оси Y
сдвиг графика вниз по оси Y
· 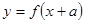 сдвиг графика влево по оси Х
сдвиг графика влево по оси Х
·  сдвиг графика вправо по оси Х
сдвиг графика вправо по оси Х
·  сжатие или растяжение графика от оси X
сжатие или растяжение графика от оси X
· 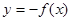 симметрия (отражение) графика относительно оси Х
симметрия (отражение) графика относительно оси Х
·  сжатие или растяжение графика от оси Y ( при к > 1 –сжатие, при k < 1- растяжение)
сжатие или растяжение графика от оси Y ( при к > 1 –сжатие, при k < 1- растяжение)
·  симметрия (отражение) графика относительно оси Y
симметрия (отражение) графика относительно оси Y
· 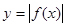 симметрия относительно оси Х
симметрия относительно оси Х
·  симметрия относительно оси Y
симметрия относительно оси Y
1.3. Свойства функции
Область определения и множество значений – это не свойства функции, а ее неотъемлемые атрибуты
Четность
Функция y=f(x) является:
- четной, если для любых x и -x из ООФ
 ;
; - нечетной, если для любых x и -x Î D(f)
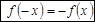 ;
; - функция, которая не является ни четной, ни нечетной – функция общего вида.
2) Периодичность
Функция y=f(x) называется периодичной, если найдется такое число Т ≠ 0, что:
1. для любой точки x Î D(f), (x + T) Î D(f) и (x – T) Î D(f)
2. f(x + T) = f(x – T) = f(x)
Число T называется периодом функции.
Монотонность
Под монотонностью понимаем постоянство поведения функции на каком-либо интервале, т.е. возрастание и убывание функции.
Пусть функция y=f(x) существует на множестве M и точки x1 , x2 Î D(f). Тогда:
- функция возрастает, если при x1 > x2 f(x1) > f(x2)
- функция убывает, если при x1 > x2 f)x1) < f(x2)
4) Нули функции. Графически – это точки, в которых график функции пересекает ось Х. Нули функции определяются составлением и решением уравнения: y=f(x)=0.
5) Наличие экстремумов
6) Ограниченность (или наличие наибольшего и наименьшего значений функции). Это свойство функции, при котором множество ее значений ограничено. Не любая функция ограничена. Например, функция  ограничена снизу. Графиком данной функции является парабола, ветви которой направлены вверх, т.к. старший коэффициент положителен. Функция
ограничена снизу. Графиком данной функции является парабола, ветви которой направлены вверх, т.к. старший коэффициент положителен. Функция  ограничена сверху. Функция
ограничена сверху. Функция  ограничена значениями от -1 до 1.
ограничена значениями от -1 до 1.
7) Асимптоты графика. Это прямые, к которым график функции бесконечно приближается, но никогда не пересекает. Нахождение асимптот рассмотрено в теме «Дифференциальное исчисление».
8) Обратимость.
1.4. Виды функций
Числовая последовательность
Последовательность можно понимать как частный вид функций, а именно как функцию номера места члена последовательности  . Обозначение числовой последовательности -
. Обозначение числовой последовательности - 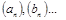 или
или 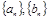 , где n – номер члена последовательности, an – общий член последовательности.
, где n – номер члена последовательности, an – общий член последовательности.
Sn – последовательность сумм.  .
.
Примеры числовых последовательностей:
-
 ;
; -
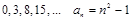 ;
; -
 и т.д.
и т.д.
Способ задания последовательности, при котором для вычисления n-го члена надо знать предыдущие, называется рекуррентным.
1.4.2. Основные элементарные функции
· Степенная:  ;
;
· Рациональная (это комбинация степенных с коэффициентами): 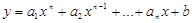 ;
;
· Показательная:  ;
;
· Логарифмическая:  ;
;
· Тригонометрические:  ;
;
· Обратные тригонометрические: 
1.4.3. Сложная функция
Это функция, аргументом которой тоже является функция.
Пусть u = g(x) – функция, определенная на множестве D(u) и со значениями E(u),
y = f(u) – функция, определенная на множестве E(u). Тогда каждому xÎD(u) можно поставить в соответствие: x ——g—> g(x) ——f—> f(g(x))
Тогда 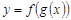 – сложная функция (или композиция функций f ○ g).
– сложная функция (или композиция функций f ○ g).
При этом u = g(x) – внутренняя функция, y = f(u) – внешняя функция.
Например: 1) y = (3x – 5)5 u = 3x – 5 – внутренняя, y = u5 – внешняя
2) y = cos(1 – x2) u = 1 – x2 – внутренняя, y = cos u – внешняя.
Обратная функция
Чтобы функция имела обратную, она должна быть обратимой.
Функция  с областью определения
с областью определения  и множеством значений
и множеством значений  называется обратимой, если для любых
называется обратимой, если для любых 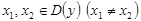 выполняется условие
выполняется условие  .
.
Примеры обратных функций:
1) Для функции  - обратная функция;
- обратная функция;
2) Функция 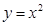 необратима на множестве (- ∞; ∞), но обратима на множестве
необратима на множестве (- ∞; ∞), но обратима на множестве  .
.
Графики взаимно обратных функций симметричны относительно прямой y = x (биссектрисы первой и третьей четвертей).
Композиция двух взаимно обратных функций всегда равна аргументу. Например: