1.1. Числовая последовательность
Последовательность можно понимать как частный вид функций, а именно как функцию номера места члена последовательности 
. Обозначение числовой последовательности - 
или 
, где n – номер члена последовательности, an – общий член последовательности.
Sn – последовательность сумм. 
.
Примеры числовых последовательностей:
-
; -
; -
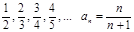и т.д.
Способ задания последовательности, при котором для вычисления n-го члена надо знать предыдущие, называется рекуррентным.
К известным рекуррентным соотношениям относят:
· Арифметическую прогрессию (an ) – 
, d – разность прогрессии.
Например, сумма n первых натуральных чисел: 
;
· Геометрическую прогрессию (bn) – 
, q – знаменатель прогрессии. При | q | < 1 получаем бесконечно убывающую геометрическую прогрессию;
· Последовательность Фибоначчи. Если взять a1=1, a2=2, то получится стандартная последовательность чисел Фибоначчи: 1, 2, 3, 5, 8, 11, 21, … Здесь 
, т.е. задается с a3. Формула общего члена: 
· Последовательность факториалов. Приняв a1=1, an является произведением натуральных чисел от 1 до n: 
. Восклицательный знак – это обозначение факториала. Например: 
.Формула общего члена: 
.
Конечно, существует бесконечно много различных числовых последовательностей.
1.2. Свойства последовательностей.
· Над последовательностями можно производить арифметические операции: сложение (вычитание) и умножение (деление);
· Возрастающая последовательность – последовательность, в которой каждый последующий член больше предыдущего, т.е. для любого 
.
Убывающая последовательность – соответственно для любого 
.
Монотонная последовательность – это последовательность, которая является либо возрастающей, либо убывающей.
· Ограниченные последовательности. Последовательность 
называется ограниченной, если для ее членов можно указать общую границу, т.е. такое число С, что для всех номеров n выполняется неравенство: 
.
Возрастающая последовательность ограничена сверху, если для всех n 
;
Убывающая последовательность ограничена снизу, если для всех n 
;
Чтобы последовательность была ограниченной, необходимо, чтобы она была ограничена и сверху и снизу.
1.3. Предел последовательности
Число A называют пределом последовательности a1,a2,…, если начиная с некоторого момента все члены этой последовательности, будут сколь угодно мало отличаться от A. 
Произношение: предел последовательности an при n стремящемся к бесконечности; lim - от латинского «лимит».
Последовательности, которые имеют пределы, называются сходящимися, а которые не имеют – расходящимися.
Правила вычисления пределов:
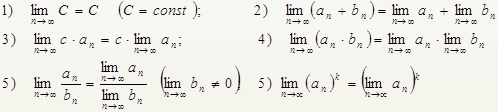
Примеры вычисления пределов последовательностей
В приведенных примерах: первые четыре – сходящиеся последовательности, т.к. имеют конечный предел, а пятая – расходящаяся последовательность.
Признак сходимости последовательности. Если последовательность монотонна и ограничена, то она имеет предел.
К явно сходящимся последовательностям относится и бесконечно убывающая геометрическая прогрессия. Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле: 
1.4. Бесконечно малые и бесконечно большие функции
1.4.1. Окрестность точки
Определение. Дельта (δ) - окрестностью точки a называется множество точек пространства, удаленных от точки a на расстояние меньшее, чем δ, т.е. 
1.4.2. Бесконечно Малые Функции (Б.М.Ф.)
Определение. Функция α(x) называется бесконечно малой в точке а (или при x→a), если для всякого сколь угодно малого числа ε >0 можно указать такую δ - окрестность точки а, что для всех x, попадающих в эту окрестность, выполняется неравенство 
.
Т.е. если: 
то: 
Примеры Б.М.Ф.
1) y = x – 2 Б.М.Ф. в точке x = 2 (можно записать: при x→2 y→0)
2 ) y = sin x Б.М.Ф. в точке x = 0, π, 2π…
3) 
Б.М.Ф. в точке x = 2
1.4.3. Бесконечно Большие Функции (Б.Б.Ф.)
Определение. Функция Φ(x) называется бесконечно большой при x→a, если Φ(x) ≠ 0 в некоторой окрестности точки а и 1/ Φ(x) является б.м.ф. (x→a).
Запись: при Φ(x) > 0 
; при Φ(x) < 0 
Например, функция (см. рис.)
(x≠1) является б.б.ф. при x→1, т.е. 
Это очевидно, т.к. 1/Φ(x) = (x – 1)2 – б.м.ф. при x→1
Если f(x) – бесконечно большая функция в окрестности точки a, тогда график функции в этой точке «взвивается» вверх (на +∞) или резко уходит вниз (на −∞). Прямая x=a называется вертикальной асимптотой графика.
1.5. Практическая работа № 4 «Числовые последовательности»
1.5.1. Найдите 4-й член последовательности, если последовательность задана формулой:
1.5.2. Найдите предел последовательности, заданной формулой общего члена:
;
1.5.3.. Найдите сумму членов бесконечно убывающей геометрическойпрогрессии: 