Возможны два случая нарушения сбалансированности. Первый из них исправляется 1 и 3 типом, а второй – 2 и 4. Рассмотрим первый случай. Пусть имеется следующее сбалансированное поддерево:
Поддерево. Случай 1
Здесь x и y – узлы, а A, B, C – поддеревья. После добавления к поддереву A узла v, баланс нарушиться, и потребуется балансировка. Она осуществляется правым поворотом (тип 1) узла y:
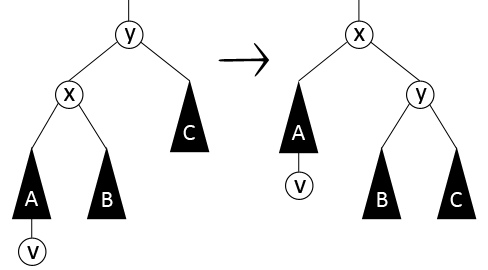Малый правый поворот
Малое левое вращение выполняется симметрично малому правому. Следующие две функции выполняют малый правый и малый левый повороты.
Node* RightRotation(Node *x) { Node *y=x->left; x->left=y->right; y->right=x; OverHeight(x); OverHeight(y); return y; } Node *LeftRotation(Node *y) { Node *x=y->right; y->right=x->left; x->left=y; OverHeight(y); OverHeight(x); return x; }
| Node* RightRotation(Node *x) { Node *y=x->left; x->left=y->right; y->right=x; OverHeight(x); OverHeight(y); return y; } Node *LeftRotation(Node *y) { Node *x=y->right; y->right=x->left; x->left=y; OverHeight(y); OverHeight(x); return x; } |
Второй случай дисбаланса исправляется большим правым или большим левым вращением. Пусть имеется следующее сбалансированное поддерево:
Поддерево. Случай 2
Вставка узлов в поддерево A или D, не нарушит сбалансированности, но добавление их в B или C приведет к необходимости произвести балансировку вращением 2-ого типа:
Большое левое вращение выполняется симметрично большому правому. Функция Balance выполняет балансировку узла путем вращения его поддеревьев:
Node *Balance(Node *x) { OverHeight(x); if (BF(x)==2) { if (BF(x->right)<0) x->right=RightRotation(x->right); return LeftRotation(x); } if (BF(x)==-2) { if (BF(x->left)>0) x->left=LeftRotation(x->left); return RightRotation(x); } return x; }
| Node *Balance(Node *x) { OverHeight(x); if (BF(x)==2) { if (BF(x->right)<0) x->right=RightRotation(x->right); return LeftRotation(x); } if (BF(x)==-2) { if (BF(x->left)>0) x->left=LeftRotation(x->left); return RightRotation(x); } return x; } |
Данная функция проверяет условия, и в зависимости от результата балансирует узел x, применяя один из типов вращения.
Добавление узлов
Операция вставки нового узла в АВЛ-дерево выполняется рекурсивно. По ключу данного узла, производиться поиск места вставки: спускаясь вниз по дереву, алгоритм сравнивает ключ добавляемого узла со встречающимися ключами, далее происходит вставка нового элемента; по возвращению из рекурсии, выполняется проверка всех показателей сбалансированности узлов и, в случае необходимости, выполняется балансировка. Для осуществления балансировки следует знать, с каким из рассмотренных выше случаев дисбаланса имеем дело. Допустим, мы добавили узел x в левое поддерево, для которого выполнялось h(Ti, R) < h(Ti, L), т. е. высота левого поддерева изначально превышала высоту правого. Если левое поддерево этого узла выше правого, то потребуется большое вращение, иначе – малое.
Функция добавления узла:
Node *Insert(Node *x, int k) { if (!x) return new Node(k); if (k<x->key) x->left=Insert(x->left, k); else x->right=Insert(x->right, k); return Balance(x); }
| Node *Insert(Node *x, int k) { if (!x) return new Node(k); if (k<x->key) x->left=Insert(x->left, k); else x->right=Insert(x->right, k); return Balance(x); } |
Удаление узлов.
Также как и вставку узла, его удаление удобно задать рекурсивно. Пусть x – удаляемый узел, тогда если x – лист (терминальный узел), то алгоритм удаления сводиться к простому исключению узла x, и подъему к корню с переопределением balance factor’ов узлов. Если же x не является листом, то он либо имеет правое поддерево, либо не имеет его. Во втором случае, из свойства АВЛ-дерева, следует, что левое поддерево имеет высоту 1, и здесь алгоритм удаления сводиться к тем же действиям, что и при терминальном узле. Остается ситуация когда у x есть правое поддерево. В таком случае нужно в правом поддереве отыскать следующий по значению за x узел y, заменить x на y, и рекурсивно вернуться к корню, переопределяя коэффициенты сбалансированности узлов. Из свойства двоичного дерева поиска следует, что узел y имеет наименьшее значение среди всех узлов правого поддерева узла x.
Для программной реализации операции удаления узла опишем функцию Delete:
Node *Delete(Node *x, int k) { if (!x) return 0; if (k<x->key) x->left=Delete(x->left, k); else if (k>x->key) x->right=Delete(x->right, k); else { Node *y=x->left; Node *z=x->right; delete x; if (!z) return y; Node* min=SearchMin(z); min->right=DeleteMin(z); min->left=y; return Balance(min); } return Balance(x); }
| Node *Delete(Node *x, int k) { if (!x) return 0; if (k<x->key) x->left=Delete(x->left, k); else if (k>x->key) x->right=Delete(x->right, k); else { Node *y=x->left; Node *z=x->right; delete x; if (!z) return y; Node* min=SearchMin(z); min->right=DeleteMin(z); min->left=y; return Balance(min); } return Balance(x); } |
Из нее вызываются вспомогательные функции: SearchMin и DeleteMin. Первая ищет минимальный элемент в правом поддереве, вторая удаляет его. Опишем эти вспомогательные функции:
Node *SearchMin(Node *x) { if (x->left) return SearchMin(x->left); else return x; } Node *DeleteMin(Node *x) { if (x->left==0) return x->right; x->left=DeleteMin(x->left); return Balance(x); }
| Node *SearchMin(Node *x) { if (x->left) return SearchMin(x->left); else return x; } Node *DeleteMin(Node *x) { if (x->left==0) return x->right; x->left=DeleteMin(x->left); return Balance(x); } |
Операция удаления реализуется определенно сложнее, чем операция добавления. Да и последствия ее выполнения могут потребовать поворота в каждом узле. Но какова вероятность возникновения ситуации, при которой появится потребность в поворотах? Этим вопросом задается Никлаус Вирт в своей книге «Алгоритмы и структуры», и отвечает на него: «Удивительный результат эмпирических проверок показал, что в то время как один поворот вызывается приблизительно каждыми двумя включениями, тем не менее, при удалении мы имеем дело с одним поворотом на целых пять удалений