Вспомогательные материалы для выполнения задания по дисциплине «Теория алгоритмов»
Список смежности графа.
По отношению к памяти списки смежности менее требовательны, чем матрицы смежности, для их хранения нужно O(|V|+|E|) памяти. Такой список графически можно изобразить в виде таблицы, столбцов в которой – два, а строк не больше чем вершин в графе. В качестве примера возьмем смешанный граф: 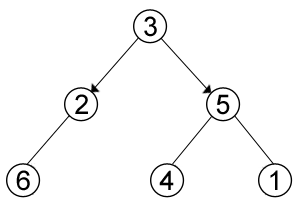
В нем 6 вершин (|V|) и 5 ребер (|E|). Из последних 2 ребра направленные и 3 ненаправленные, и, причем из каждой вершины выходит, как минимум одно ребро в другую вершину, из чего следует, что в списке смежности этого графа будет |V| строк.
смежности этого графа будет |V| строк.
| Вершина выхода | Вершины входа |
| 2, 5 | |
| 1, 4 | |
В i строке и 1 столбце указана вершина выхода, а в i строке и 2 столбце – вершина входа. Так, к примеру, из вершины 5 выходят два ребра, входящие в вершины 1 и 4.
Теперь перейдем непосредственно к программной реализации списка смежности. Количество вершин и ребер будут задаваться с клавиатуры, поэтому установим ограничения, иначе говоря, определим две константы, одна из которых отвечает за максимально возможное число вершин (Vmax), другая – ребер (Emax).
Далее, нам понадобятся три одномерных целочисленных массива:
- terminal[1..Emax] – хранит вершины, в которые входят ребра;
- next [1..Emax] – содержит указатели на элементы массива terminal;
- head[1..Vmax] – содержит указатели на начала подсписков, т. е. на такие вершины записанные в массив terminal, с которых начинается процесс перечисления всех вершин смежных одной i-ой вершине.
В программе позволительно выделить две основные части: ввод ребер с последующим добавлением их в список смежности, и вывод получившегося списка смежности на экран.
Код программы на C++:
C++
#include "stdafx.h" #include <iostream> using namespace std; const int Vmax=100, Emax=Vmax*2; int head[Vmax]; int next_el[Emax]; int terminal[Emax]; int n, m, i, j, k, v, u; char r; void Add(int v, int u) //добавление ребра { k=k+1; terminal[k]=u; next_el[k]=head[v]; head[v]=k; } //главная функция void main() { setlocale(LC_ALL,"Rus"); k=0; cout<<"Кол. вершин >> "; cin>>n; cout<<"Кол. ребер >> "; cin>>m; cout<<"Вводите смежные вершины:"<<endl; for (i=0; i<m; i++) { cin>>v>>u; cout<<"Ребро ориент.? (y/n) >> "; cin>>r; if (r=='y') Add(v, u); else { Add(v, u); Add(u, v); } cout<<"..."<<endl; } //вывод списка смежности cout<<"Список смежности графа:"; for (i=0; i<n+1; i++) { j=head[i]; if (i) cout<<i<<"->"; while (j>0) { if (!next_el[j]) cout<<terminal[j]; else cout<<terminal[j]<<", "; j=next_el[j]; } cout<<endl; } system("pause>>void"); }
| #include "stdafx.h" #include <iostream> using namespace std; const int Vmax=100, Emax=Vmax*2; int head[Vmax]; int next_el[Emax]; int terminal[Emax]; int n, m, i, j, k, v, u; char r; void Add(int v, int u) //добавление ребра { k=k+1; terminal[k]=u; next_el[k]=head[v]; head[v]=k; } //главная функция void main() { setlocale(LC_ALL,"Rus"); k=0; cout<<"Кол. вершин >> "; cin>>n; cout<<"Кол. ребер >> "; cin>>m; cout<<"Вводите смежные вершины:"<<endl; for (i=0; i<m; i++) { cin>>v>>u; cout<<"Ребро ориент.? (y/n) >> "; cin>>r; if (r=='y') Add(v, u); else { Add(v, u); Add(u, v); } cout<<"..."<<endl; } //вывод списка смежности cout<<"Список смежности графа:"; for (i=0; i<n+1; i++) { j=head[i]; if (i) cout<<i<<"->"; while (j>0) { if (!next_el[j]) cout<<terminal[j]; else cout<<terminal[j]<<", "; j=next_el[j]; } cout<<endl; } system("pause>>void"); } |
Код программы на Pascal:
Delphi/Pascal
program listAdj; uses crt; Const Vmax=100; Emax=Vmax*2; Var head: array [1..Vmax] of integer; next: array [1..Emax] of integer; terminal: array [1..Emax] of integer; n, m, i, j, k, v, u: integer; r: char; {добавление ребер} procedure Add(v, u: integer); begin k:=k+1; terminal[k]:=u; next[k]:=head[v]; head[v]:=k; end; {начало основной программы} begin clrscr; k:=0; write('Кол. вершин >> '); read(n); write('Кол. ребер >> '); read(m); writeln('Вводите смежные вершины:'); for i:=1 to m do begin read(v, u); write('Ребро ориент.? (y/n) >> '); read(r); if r='y' then add(v, u) else begin add(v, u); add(u, v); end; writeln('...'); end; {вывод списка смежности} writeln('Список смежности графа:'); for i:=1 to n do begin j:=head[i]; write(i, '->'); while j>0 do begin if next[j]=0 then write(terminal[j]) else write(terminal[j], ', '); j:=next[j]; end; writeln; end; end.
| program listAdj; uses crt; Const Vmax=100; Emax=Vmax*2; Var head: array [1..Vmax] of integer; next: array [1..Emax] of integer; terminal: array [1..Emax] of integer; n, m, i, j, k, v, u: integer; r: char; {добавление ребер} procedure Add(v, u: integer); begin k:=k+1; terminal[k]:=u; next[k]:=head[v]; head[v]:=k; end; {начало основной программы} begin clrscr; k:=0; write('Кол. вершин >> '); read(n); write('Кол. ребер >> '); read(m); writeln('Вводите смежные вершины:'); for i:=1 to m do begin read(v, u); write('Ребро ориент.? (y/n) >> '); read(r); if r='y' then add(v, u) else begin add(v, u); add(u, v); end; writeln('...'); end; {вывод списка смежности} writeln('Список смежности графа:'); for i:=1 to n do begin j:=head[i]; write(i, '->'); while j>0 do begin if next[j]=0 then write(terminal[j]) else write(terminal[j], ', '); j:=next[j]; end; writeln; end; end. |
Работа двух приведенных программ идентична, а отличаются они друг от друга, лишь символикой, используемой в ЯП, поэтому дальнейшие рассуждения будут касаться их обеих. Итак, первое действие, на которое стоит обратить внимание это запрос на ввод суммы вершин (n) и ребер (m) графа (пользователь должен заранее знать эти данные).
Далее, запускается цикл ввода ребер (смежных вершин). Условие в этом цикле нужно для того, чтобы узнать, какое введено ребро. Если введено направленное ребро, то функция add вызывается 1 раз, иначе – 2, тем самым внося сведения, что есть ребро как из вершины v в вершину u, так и из u в v. После того как список смежности сформирован, программа выводит его на экран.
Для этого использован цикл от 1 до n, где n – количество вершин, а также вложенный в него цикл, который прекращает свою работу тогда, когда указатель на следующий элемент для i-ой вершины отсутствует, т. е. все смежные ей вершины уже выведены.
Функция add производит добавление ребер в изначально пустой список смежности:
Add(v, u)
k:=k+1
terminal[k]:=u
next[k]:=head[v]
head[v]:=k
Чтобы сделать это, производятся операции с формальными параметрами, вспомогательной переменной k и тремя одномерными целочисленными массивами. Значение переменной k увеличивается на 1. Затем в k-ый элемент массива terminal записывается конечная для некоторого ребра вершина (u). В третий строке k-ому элементу массива next присваивается адрес следующего элемента массива terminal. Ну и в конце массив head заполняется указателями на стартовые элементы, те с которых начинается подсписок (строка в таблице) смежных вершин с некоторой i-ой вершиной.
Так как в ячейке на пересечении i-ой строки и 2-ого столбца могут быть записаны несколько элементов (что соответствует нескольким смежным вершинам) назовем каждую строку в списке смежности его подсписком. Таким образом, в выведенном списке смежности, элементы подсписков будут отсортированы в обратном порядке. Но, как правило, порядок вывода смежных вершин (в подсписках) попросту неважен
Список ребер графа.
Список, в каждой строке которого записаны две смежные вершины и вес, соединяющего их ребра, называется списком ребер графа. Возьмем связный граф G=(V, E), и множество ребер E разделим на два класса d и k, где d – подмножество, включающее только неориентированные ребра графа G, а k – ориентированные
Предположим, что некоторая величина p соответствует количеству всех ребер, входящих в подмножество d, а s – тоже относительно k. Тогда для графа G высота списка ребер будет равна s+p*2. Иными словами, количество строк в списке ребер всегда должно быть равно величине, получающейся в результате сложения ориентированных ребер с неориентированными, увеличенными вдвое.
Это утверждение следует из сказанного ранее, а именно, что данный способ представления графа предусматривает хранение в каждой строке двух смежных вершин, а неориентированное ребро, соединяющее вершины v и u, идет как из v в u, так и из u в v.
Рассмотрим смешанный граф, в котором 5 вершин, 4 ребра и каждому ребру поставлено в соответствие некоторое целое значение (для наглядности оно составлено из номеров вершин):

В нем 3 направленных ребра и 1 ненаправленное. Подставив значения в формулу, получим высоту списка ребер: 3+1*2=5.
Так выглядит список ребер для приведенного графа. Это таблица размером n×3, где n= s+p*2=3+1*2=5. Элементы первого столбца располагаются в порядке возрастания, в то время как порядок элементов второго столбца зависит от первого, а третьего от двух предыдущих.
Программная реализация списка ребер похожа на реализацию списка смежности. Так же как и в последней, в ней изначально необходимо организовать ввод данных, которые при помощи специальной функции будут распределяться по массивам. Второй шаг – вывести получившийся список смежности на экран.
В списке смежности хранились только смежные вершины, а здесь, помимо них, будут храниться веса инцидентных этим вершинам ребер, и для этой цели понадобиться дополнительный массив. К тому же, данный метод требует более строго порядка вывода вершин, т. к. если в списке смежности последовательность нарушалась лишь в строках, то использование аналогичного способа построения приведет к нарушению порядка в столбцах. Поэтому функцию добавления ребер следует организовать иначе.
Код программы на C++:
C++
#include "stdafx.h" #include <iostream> using namespace std; const int Vmax=100, Emax=Vmax*(Vmax-1)/2; //в случае, если граф полный int terminal[Emax], weight[Emax], point[Emax]; int head[Vmax], last[Vmax]; int n, m, v, u, w, k=0, i; char r; void Add(int v, int u, int w) //добавление ребра { k=k+1; terminal[k]=u; weight[k]=w; //если вершина v новая, то //первая смежная ей вершина имеет номер k if (head[v]==0) head[v]=k; //если вершина v уже просматривалась, то //следующая смежная с ней вершина имеет номер k if (last[v]!=0) point[last[v]]=k; last[v]=k; } //главная функция void main() { setlocale(LC_ALL,"Rus"); cout<<"Кол. вершин >> "; cin>>n; cout<<"Кол. ребер >> "; cin>>m; cout<<"Вводите ребра и их вес (v, u, w):\n"; for (i=0; i<m; i++) { cin>>v>>u>>w; cout<<"Ребро ориент.? (y/n) >> "; cin>>r; if (r=='y') Add(v, u, w); else { Add(v, u, w); Add(u, v, w); } cout<<"..."<<endl; } m=m*2; //вывод списка ребер cout<<"Список ребер графа:\n"; for (i=0; i<m; i++) { k=head[i]; while (k>0) { cout<<"("<<i<<"->"<<terminal[k]<<")$="<<weight[k]<<endl; k=point[k]; } } system("pause>>void"); }
| #include "stdafx.h" #include <iostream> using namespace std; const int Vmax=100, Emax=Vmax*(Vmax-1)/2; //в случае, если граф полный int terminal[Emax], weight[Emax], point[Emax]; int head[Vmax], last[Vmax]; int n, m, v, u, w, k=0, i; char r; void Add(int v, int u, int w) //добавление ребра { k=k+1; terminal[k]=u; weight[k]=w; //если вершина v новая, то //первая смежная ей вершина имеет номер k if (head[v]==0) head[v]=k; //если вершина v уже просматривалась, то //следующая смежная с ней вершина имеет номер k if (last[v]!=0) point[last[v]]=k; last[v]=k; } //главная функция void main() { setlocale(LC_ALL,"Rus"); cout<<"Кол. вершин >> "; cin>>n; cout<<"Кол. ребер >> "; cin>>m; cout<<"Вводите ребра и их вес (v, u, w):\n"; for (i=0; i<m; i++) { cin>>v>>u>>w; cout<<"Ребро ориент.? (y/n) >> "; cin>>r; if (r=='y') Add(v, u, w); else { Add(v, u, w); Add(u, v, w); } cout<<"..."<<endl; } m=m*2; //вывод списка ребер cout<<"Список ребер графа:\n"; for (i=0; i<m; i++) { k=head[i]; while (k>0) { cout<<"("<<i<<"->"<<terminal[k]<<")$="<<weight[k]<<endl; k=point[k]; } } system("pause>>void"); } |
Код программы на Pascal:
Delphi/Pascal
program ListEdges; uses crt; const Vmax=100; Emax=Vmax*(Vmax-1) div 2; {в случае, если граф полный} Var terminal, weight, point: array [1..Emax] of integer; head, last: array [1..Vmax] of integer; n, m, v, u, w, k, i: integer; yn: char; procedure Add(v, u, w: integer); begin k:=k+1; terminal[k]:=u; weight[k]:=w; {если вершина v новая, то первая смежная ей вершина имеет номер k} if head[v]=0 then head[v]:=k; {если вершина v уже просматривалась, то следующая смежная с ней вершина имеет номер k} if last[v]<>0 then point[last[v]]:=k; last[v]:=k; end; {основной блок программы} begin clrscr; write('Количество вершин > '); read(n); write('Количество ребер > '); read(m); {ввод ребер} writeln('Вводите ребра и их вес (v, u, w) > '); for i:=1 to m do begin read(v, u, w); write('Ребро ориентир.? (y/n) > '); read(yn); if yn='n' then begin Add(v, u, w); Add(u, v, w); end else begin Add(v, u, w); end; end; m:=m*2; {вывод списка ребер} writeln('Список ребер:'); for i:=1 to m do begin k:=head[i]; while (k>0) do begin writeln('(', i, '->', terminal[k], ')$=', weight[k]); k:=point[k]; end; end; end.
| program ListEdges; uses crt; const Vmax=100; Emax=Vmax*(Vmax-1) div 2; {в случае, если граф полный} Var terminal, weight, point: array [1..Emax] of integer; head, last: array [1..Vmax] of integer; n, m, v, u, w, k, i: integer; yn: char; procedure Add(v, u, w: integer); begin k:=k+1; terminal[k]:=u; weight[k]:=w; {если вершина v новая, то первая смежная ей вершина имеет номер k} if head[v]=0 then head[v]:=k; {если вершина v уже просматривалась, то следующая смежная с ней вершина имеет номер k} if last[v]<>0 then point[last[v]]:=k; last[v]:=k; end; {основной блок программы} begin clrscr; write('Количество вершин > '); read(n); write('Количество ребер > '); read(m); {ввод ребер} writeln('Вводите ребра и их вес (v, u, w) > '); for i:=1 to m do begin read(v, u, w); write('Ребро ориентир.? (y/n) > '); read(yn); if yn='n' then begin Add(v, u, w); Add(u, v, w); end else begin Add(v, u, w); end; end; m:=m*2; {вывод списка ребер} writeln('Список ребер:'); for i:=1 to m do begin k:=head[i]; while (k>0) do begin writeln('(', i, '->', terminal[k], ')$=', weight[k]); k:=point[k]; end; end; end. |
Максимально возможное количество вершин в графе задано константой Vmax, а ребер – Emax. Последняя константа инициализируется формулой Vmax*(Vmax-1)/2, вычисляющей количество ребер в полном графе при известном числе вершин.
Далее, в программах описываются 5 массивов:
terminal – массив вершин, в которые входят ребра;
weight – массив весов ребер;
head[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – первая вершина смежная с i-ой, а weight[k] – вес инцидентного ей ребра;
last[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – последняя вершина смежная с i-ой, а weight[k] – вес инцидентного ей ребра;
point[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – следующая вершина смежная с i-ой, а weight[k] – вес инцидентного ей ребра.
После ввода количества вершин (n) и ребер (m) графа, запускается цикл, на каждом шаге которого пользователь вводит с клавиатуры две смежные вершины и вес, лежащего между ними ребра. Если ребро является ориентированным, то функция добавления данных в список ребер (Add) вызывается один раз, если неориентированным – два раза. Общее число вызовов функции вычисляется все по той же формуле s+(p*2), где s – ориентированные ребра графа, p – неориентированные. Закончив формирование списка ребер, необходимо вдвое увеличить переменную m, т. к. в случае чисто неориентированного графа высота списка будет равна 0+(m*2).
Осталось вывести на экран получившуюся конструкцию. Вспомним, что на номер первой вершины смежной с i-ой вершиной указывает элемент head[i], следовательно, каждая новая итерация внешнего цикла должна начинаться с взятия этого номера (k=head[i]). Внутренний цикл перестанет выполняться тогда, когда не найдется ни одной смежной с i-ой вершины (k станет равной нулю), а внешний – по окончанию вывода списка ребер
Основные структуры данных.
Необходимым условием хранения информации в памяти компьютера является возможность преобразования этой самой информации в подходящую для компьютера форму. В том случае, если это условие выполняется, следует определить структуру, пригодную именно для наличествующей информации, ту, которая предоставит требующийся набор возможностей работы с ней.
 Кольцевой список
Кольцевой список
Здесь под структурой понимается способ представления информации, посредством которого совокупность отдельно взятых элементов образует нечто единое, обусловленное их взаимосвязью друг с другом. Скомпонованные по каким-либо правилам и логически связанные межу собой, данные могут весьма эффективно обрабатываться, так как общая для них структура предоставляет набор возможностей управления ими – одно из того за счет чего достигаются высокие результаты в решениях тех или иных задач.
Но не каждый объект представляем в произвольной форме, а возможно и вовсе для него имеется лишь один единственный метод интерпретации, следовательно, несомненным плюсом для программиста будет знание всех существующих структур данных. Таким образом, часто приходиться делать выбор между различными методами хранения информации, и от такого выбора зависит работоспособность продукта.
Говоря о не вычислительной технике, можно показать ни один случай, где у информации видна явная структура. Наглядным примером служат книги самого разного содержания. Они разбиты на страницы, параграфы и главы, имеют, как правило, оглавление, то есть интерфейс пользования ими. В широком смысле, структурой обладает всякое живое существо, без нее органика навряд-ли смогла бы существовать.
Вполне вероятно, читателю приходилось сталкиваться со структурами данных непосредственно в информатике, например, с теми, что встроены в язык программирования. Часто они именуются типами данных. К таковым относятся: массивы, числа, строки, файлы и т. д.
Методы хранения информации, называемые «простыми», т. е. неделимыми на составные части, предпочтительнее изучать вместе с конкретным языком программирования, либо же глубоко углубляться в суть их работы. Поэтому здесь будут рассмотрены лишь «интегрированные» структуры, те которые состоят из простых, а именно: массивы, списки, деревья и графы.
Массивы.
Массив – это структура данных с фиксированным и упорядоченным набором однотипных элементов (компонентов). Доступ к какому-либо из элементов массива осуществляется по имени и номеру (индексу) этого элемента. Количество индексов определяет размерность массива. Так, например, чаще всего встречаются одномерные (вектора) и двумерные (матрицы) массивы.
Первые имеют один индекс, вторые – два. Пусть одномерный массив называется A, тогда для получения доступа к его i-ому элементу потребуется указать название массива и номер требуемого элемента: A[i]. Когда A – матрица, то она представляема в виде таблицы, доступ к элементам которой осуществляется по имени массива, а также номерам строки и столбца, на пересечении которых расположен элемент: A[i, j], где i – номер строки, j – номер столбца.
В разных языках программирования работа с массивами может в чем-то различаться, но основные принципы, как правило, везде одни. В языке Pascal, обращение к одномерному и двумерному массиву происходит точно так, как это показано выше, а, например, в C++ двумерный массив следует указывать так: A[i][j]. Элементы массива нумеруются поочередно. На то, с какого значения начинается нумерация, влияет язык программирования. Чаще всего этим значением является 0 или 1.
Массивы, описанного типа называются статическими, но существуют также массивы по определенным признакам отличные от них: динамические и гетерогенные. Динамичность первых характеризуется непостоянностью размера, т. е. по мере выполнения программы размер динамического массива может изменяться. Такая функция делает работу с данными более гибкой, но при этом приходится жертвовать быстродействием, да и сам процесс усложняется.
Обязательный критерий статического массива, как было сказано, это однородность данных, единовременно хранящихся в нем. Когда же данное условие не выполняется, то массив является гетерогенным. Его использование обусловлено недостатками, которые имеются в предыдущем виде, но оно оправданно во многих случаях.
Таким образом, даже если Вы определились со структурой, и в качестве нее выбрали массив, то этого все же недостаточно. Ведь массив это только общее обозначение, род для некоторого числа возможных реализаций. Поэтому необходимо определиться с конкретным способом представления, с наиболее подходящим массивом.
Списки.
Список – абстрактный тип данных, реализующий упорядоченный набор значений. Списки отличаются от массивов тем, что доступ к их элементам осуществляется последовательно, в то время как массивы – структура данных произвольного доступа. Данный абстрактный тип имеет несколько реализаций в виде структур данных. Некоторые из них будут рассмотрены здесь.
Список (связный список) – это структура данных, представляющая собой конечное множество упорядоченных элементов, связанных друг с другом посредствам указателей. Каждый элемент структуры содержит поле с какой-либо информацией, а также указатель на следующий элемент. В отличие от массива, к элементам списка нет произвольного доступа.
 Односвязный список
Односвязный список
В односвязном списке, приведенным выше, начальным элементом является Head list (голова списка [произвольное наименование]), а все остальное называется хвостом. Хвост списка составляют элементы, разделенные на две части: информационную (поле info) и указательную (поле next). В последнем элементе вместо указателя, содержится признак конца списка – nil.
Односвязный список не слишком удобен, т. к. из одной точки есть возможность попасть лишь в следующую точку, двигаясь тем самым в конец. Когда кроме указателя на следующий элемент есть указатель и на предыдущий, то такой список называется двусвязным.
 Двусвязный список
Двусвязный список
Возможность двигаться как вперед, так и назад полезна для выполнения некоторых операций, но дополнительные указатели требуют задействования большего количества памяти, чем таковой необходимо в эквивалентном односвязном списке.
Для двух видов списков описанных выше существует подвид, называемый кольцевым списком. Сделать из односвязного списка кольцевой можно добавив всего лишь один указатель в последний элемент, так чтобы он ссылался на первый. А для двусвязного потребуется два указателя: на первый и последний элементы.
 Кольцевой список
Кольцевой список
Помимо рассмотренных видов списочных структур есть и другие способы организации данных по типу «список», но они, как правило, во многом схожи с разобранными, поэтому здесь они будут опущены.
Кроме различия по связям, списки делятся по методам работы с данными. О некоторых таких методах сказано далее.
Стек.
 Стек
Стек
Стек характерен тем, что получить доступ к его элементом можно лишь с одного конца, называемого вершиной стека, иначе говоря: стек – структура данных, функционирующая по принципу LIFO (last in — first out, «последним пришёл — первым вышел»). Изобразить эту структуру данных лучше в виде вертикального списка, например, стопки каких-либо вещей, где чтобы воспользоваться одной из них нужно поднять все те вещи, что лежат выше нее, а положить предмет можно лишь на вверх стопки.
В показанном односвязном списке операции над элементами происходят строго с одного конца: для включения нужного элемента в пятую по счету ячейку необходимо исключить тот элемент, который занимает эту позицию. Если бы было, например 6 элементов, а вставить конкретный элемент требовалось также в пятую ячейку, то исключить бы пришлось уже два элемента.
Очередь.
Структура данных «Очередь» использует принцип организации FIFO (First In, First Out — «первым пришёл — первым вышел»). В некотором смысле такой метод более справедлив, чем тот, по которому функционирует стек, ведь простое правило, лежащее в основе привычных очередей в различные магазины, больницы считается вполне справедливым, а именно оно является базисом этой структуры. Пусть данное наблюдение будет примером. Строго говоря, очередь – это список, добавление элементов в который допустимо, лишь в его конец, а их извлечение производиться с другой стороны, называемой началом списка.
 Очередь
Очередь
Дек.
Дек (deque — double ended queue, «двухсторонняя очередь») – стек с двумя концами. Действительно, несмотря конкретный перевод, дек можно определять не только как двухстороннюю очередь, но и как стек, имеющий два конца. Это означает, что данный вид списка позволяет добавлять элементы в начало и в конец, и то же самое справедливо для операции извлечения.
 Дек
Дек
Эта структура одновременно работает по двум способам организации данных: FIFO и LIFO. Поэтому ее допустимо отнести к отдельной программной единице, полученной в результате суммирования двух предыдущих видов списка.
Графы.
Раздел дискретной математики, занимающийся изучением графов, называется теорией графов. В теории графов подробно рассматриваются известные понятия, свойства, способы представления и области применения этих математических объектов. Нас же интересует, лишь те ее аспекты, которые важны в программировании.
Граф – совокупность точек, соединенных линиями. Точки называются вершинами (узлами), а линии – ребрами (дугами).

Как показано на рисунке различают два основных вида графов: ориентированные и неориентированные. В первых ребра являются направленными, т. е. существует только одно доступное направление между двумя связными вершинами, например из вершины 1 можно пройти в вершину 2, но не наоборот. В неориентированном связном графе из каждой вершины можно пройти в каждую и обратно. Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.
Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.
Ребра графа необязательно должны быть прямыми, а вершины обозначаться именно цифрами, так как показано на рисунке. К тому же встречаются такие графы, ребрам которых поставлено в соответствие конкретное значение, они именуются взвешенными графами, а это значение – весом ребра. Когда у ребра оба конца совпадают, т. е. ребро выходит из вершины F и входит в нее, то такое ребро называется петлей.

Графы широко используются в структурах, созданных человеком, например в компьютерных и транспортных сетях, web-технологиях. Специальные способы представления позволяют использовать граф в информатике (в вычислительных машинах). Самые известные из них: «Матрица смежности», «Матрица инцидентности», «Список смежности», «Список рёбер». Два первых, как понятно из названия, для репрезентации графа используют матрицу, а два последних – список.
Деревья.
 Неупорядоченное дерево
Неупорядоченное дерево
Дерево как математический объект это абстракция из соименных единиц, встречающихся в природе. Схожесть структуры естественных деревьев с графами определенного вида говорит о допущении установления аналогии между ними. А именно со связанными и вместе с этим ациклическими (не имеющими циклов) графами. Последние по своему строению действительно напоминают деревья, но в чем то и имеются различия, например, принято изображать математические деревья с корнем расположенным вверху, т. е. все ветви «растут» сверху вниз. Известно же, что в природе это совсем не так.
Поскольку дерево это по своей сути граф, у него с последним многие определения совпадают, либо интуитивно схожи. Так корневой узел (вершина 6) в структуре дерева – это единственная вершина (узел), характерная отсутствием предков, т. е. такая, что на нее не ссылается ни какая другая вершина, а из самого корневого узла можно дойти до любой из имеющихся вершин дерева, что следует из свойства связности данной структуры. Узлы, не ссылающиеся ни на какие другие узлы, иначе говоря, ни имеющие потомков называются листьями (2, 3, 9), либо терминальными узлами. Элементы, расположенные между корневым узлом и листьями – промежуточные узлы (1, 1, 7, 8). Каждый узел дерева имеет только одного предка, или если он корневой, то не имеет ни одного.
Поддерево – часть дерева, включающая некоторый корневой узел и все его узлы-потомки. Так, например, на рисунке одно из поддеревьев включает корень 8 и элементы 2, 1, 9.
С деревом можно выполнять многие операции, например, находить элементы, удалять элементы и поддеревья, вставлять поддеревья, находить корневые узлы для некоторых вершин и др. Одной из важнейших операций является обход дерева. Выделяются несколько методов обхода. Наиболее популярные из них: симметричный, прямой и обратный обход. При прямом обходе узлы-предки посещаются прежде своих потомков, а в обратном обходе, соответственно, обратная ситуация. В симметричном обходе поочередно просматриваются поддеревья главного дерева.
Представление данных в рассмотренной структуре выгодно в случае наличия у информации явной иерархии. Например, работа с данными о биологических родах и видах, служебных должностях, географических объектах и т. п. требует иерархически выраженной структуры, такой как математические деревья