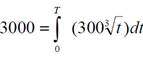1. Если начальный вклад составляет р, процентная ставка равна r, то
величина вклада через промежуток времени t определяется по формуле:
Рассмотрим обратную задачу для нахождения стоимости аннуитета (регулярных платежей) применительно к непрерывным процентам. В этом
случае платежи зависят от времени t, то есть является функцией от t, что
можно записать
Тогда величина вклада S через Т лет определяется формулой
Если рассмотреть понятия дисконтированной суммы, связанное для
непрерывных процентов с формулой
Эта формула дает возможности определять величину начального вклада p, если известно, что через t лет он должен составить величину S, а
непрерывная процентная ставка равна r. Задача аннуитета в этом случае
может быть сформулирована так: найти величину начального вклада p, если регулярные выплаты по этому вкладу должны составить S ежегодно в течение Т лет.
Расчетная формула имеет вид
Пример 6. Определить величину вклада через 2 года, если начальный капитал 50 000 ден. ед., процентная ставка 8%.
Решение. Используя формулу, получим общую величину вклада
через 2 года:
Пример 7. Требуется определить начальный вклад, если выплаты
должны составить 75 у.е. в течение трёх лет, а процентная ставка 5%.
Решение. Применим формулу
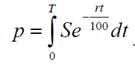
Пример 8. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 тыс. условных единиц и намечается ежегодное увеличение капиталовложения на 1 тыс. у.е.
Решение. Очевидно, что капиталовложения задаются функцией
. Тогда дисконтируемая сумма капиталовложений
Применяя формулу интегрирования по частям, получим K =30,5 тыс. усл. единиц.
|
|
Это означает, что для получения одинаковой наращиваемой суммы через три года ежегодные капиталовложения от 10 до 13 тыс. у. е. равносильны одновременным первоначальным вложениям 30,5 тыс. у. е. при той же начисляемой непрерывно процентной ставке.
Пример 9. Определить дисконтированный доход за пять года при процентной ставке 12%, если первоначальные (базовые) капиталовложения составили 8 тыс. условных единиц и намечается ежегодное увеличение капиталовложения на 8 тыс. у.е.
---------------
В курсе микроэкономики рассматриваются так называемые предельные величины, т.е. для данной величины представляемой некоторой функцией f (x), рассматривают ее производную f' (х). Поэтому часто приходится находить экономическую функцию (первообразную) по данной
функции предельных величин (производной).
Пример 10. Задана функция предельных издержек (издержки на производство дополнительной выпускаемой единицы продукции товара)
Найти функцию издержек С = С (q) и вычислить издержки в случае производства 15 единиц товара.
Решение. Находим интегрированием издержек на изготовление 15 ед. товара
Нахождение капитала по известным чистым инвестициям.
Чистыми инвестициями (капиталовложениями) называют общие инвестиции, производимые в экономике в течение определенного промежутка времени (чаще всего года), за вычетом инвестиций на возмещение выходящих из строя основных фондов (капитала).
Таким образом, за единицу времени капитал увеличивается на величину чистых инвестиций.
Если капитал обозначить как функцию времени K(t),а чистые инвестиции - I(t), сказанное выше можно записать
|
|
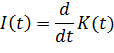
т.е. производная от капитала по времени t.
Часто требуется найти приращение капитала за период времени от t1 до t2 т.е. величину
Функция K(t) является первообразной для функции I(t), поэтому можно записать:
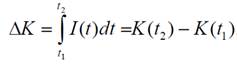
Пример 11. Заданы чистые инвестиции функцией 
Требуется определить приращение капитала за 2 года.
Пример 12. Задана функция чистых инвестиций 
Определить: сколько лет потребуется, чтобы приращение капитала составило 3000.
Решение. Обозначим искомый промежуток времени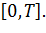 
Тогда
