Работа силы и мощность при поступательном и вращательном движениях.
Работа и мощность при поступательном движении
Работа постоянной силы P на прямолинейном участке пути s, пройденном точкой приложения силы, определяется по формуле A = Fs cos α,
где α – угол между направлением действия силы и направлением перемещения.
При α = 90°
cos α = cos 90° = 0 и A = 0,
На точку или на тело обычно действует не одна сила, а несколько, поэтому при решении задач целесообразно использовать теорему о работе равнодействующей системы сил
AR = ∑ Ai,
алгебраическая сумма работ уравновешенной системы сил на некотором пути равна нулю. ∑ Ai = 0, (при прямолинейном движении)
Мощность, развиваемая при работе постоянной силы, определяется по формуле
N = A/t или N = (Fs cos α)/t.
Если при определении работы силы Р скорость движения точки v=s/t остается постоянной, то N = Fv cos α.
Работа и мощность при вращательном движении
Величина работы пары сил измеряется произведением момента пары (вращающего момента) на угол поворота, выраженный в радианах: A = Mврφ.
Мощность при вращательном движении N = A/t = Mврφ/t.
Если тело вращается с постоянной угловой скоростью, то, заменив в формуле (2) φ/t = ω, получим N = Mврω.
Внутренние и внешние силы. Консервативные и диссипативные силы.
2. 1Внутренние и внешние силы.
1. Внешние силы—это силы, действующие на тело извне. Под влиянием внешних сил тело или начинает двигаться, если оно находилось в состоянии покоя, или изменяется скорость его движения, или направление движения. Внешние силы в большинстве случаев уравновешены другими силами и их влияние незаметно, только знание законов механики позволяет утверждать о действии внешних сил на тело, находящееся в покое.
|
|
Внешние силы, действуя на твердое тело, вызывают изменения его формы, обуславливаемые перемещением частиц.
2. Внутренними силами являются силы, действующие между частицами, эти силы оказывают сопротивление изменению формы.
Изменение формы тела под действием силы называют деформацией, а тело, претерпевшее деформацию, называют деформированным.
Равновесие внутренних сил с момента приложения внешней силы нарушается, частицы тела перемещаются одна относительно другой до такого состояния и положения, когда возникающие между ними внутренние силы уравновешивают внешние силы и тело сохраняет приобретенную деформацию.Если внутренние силы малы и окажутся неспособными уравновесить внешние силы, то тело разрушается, разъединяясь на части.
Консервативные и диссипативные силы
1. Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.
2. Неконсервативными(диссипативными) силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
Импульс тела. Закон сохранения импульса
Импульс тела
В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:
|
|
В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости
Закон сохранения импульса
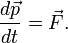В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Рассмотрим второй закон Ньютона
Перепишем его для системы из N частиц: 
где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида Fa,b и - Fb,a будут равны по абсолютному значению и противоположны по направлению, то есть Fa,b = - Fb,a Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:
.
Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.
Также стоит подчеркнуть, что изменение импульса зависит не только от действующей на тело силы, но и от продолжительности её действия
Учитывая, что лагранжиан свободной частицы имеет вид: нетрудно видеть, что последнее выражение совпадает с выражением в ньютоновом формализме: