Порядок выполнения работы. Постулаты Бора

ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА

 

Цель работы: Исследовать спектр атомарного водорода, вычислить постоянную Ридберга.

 

Приборы и принадлежности: Монохроматор, газосветные трубки с водородом.

 

 

Введение

 

Спектр испускания возникает при переходе атома из более возбуждённого состояния в менее возбуждённое. Величина испущенного кванта энергии определяется разностью энергетических уровней начального и конечного состояний.

В простейшем случае (атом водорода) сказанное можно проиллюстрировать небольшим расчётом с использованием постулатов Бора и второго закона Ньютона (сила кулоновского притяжения ядром электрона сообщает ему нормальное ускорение).

 

Постулаты Бора

 

Первый постулат

Существуют стационарные состоянии, находясь в которых, атом не излучает и не поглощает энергию.

Стационарными являются такие состояния, для которых выполняется условие:

mur = n_iħ (n_i = 1, 2, 3,…),

 

где m – масса электрона, u – скорость электрона, r – радиус его орбиты, ħ = h /(2p) = 1,03×10^-34 Дж/с – постоянная Планка.

 

Второй постулат

При переходе атома из состояния с энергией W_j в состояние с энергией W_i испускается или поглощается один фотон частотой n_Ф, энергия которого рассчитывается по формуле

E _Ф = h n_Ф = W_j - W_i.

Если W_i < W_j, происходит излучение фотона, если W_i > W_j, – поглощение фотона.

Для атома водорода уравнения, описывающие поведение электрона, имеют вид:

mur = n_iħ, (1)

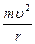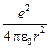= . (2)

Решая систему, можно получить значения r и u на соответствующей орбите.

Полная энергия электрона:

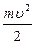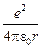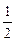
W = W _К + W _П = - = - 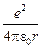. (3)

Подставив r и u из уравнений (1) – (2) в уравнение (3), получим:

W = - .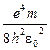

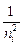Отсюда:

n_Ф = .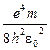

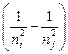Множитель 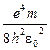обозначается буквой R и называется постоянной Ридберга; R = 3,29×10¹⁵ c^-1.

 

Линейчатые спектры обусловлены испусканием электромагнитного излучения свободными или слабо связанными атомами. Одним из источников такого излучения является возбужденный газ или пар. В данной работе используются газосветные трубки, наполненные водородом и неоном.

Установлено, что спектральные линии атомарного водорода обнаруживают несложные закономерности. Частоты соответствующих линий могут быть определены по формуле

ν = R 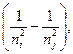(4)

 

где ν – частота, ν = c /l, с –скорость света в вакууме, λ – длина волны, R - постоянная Ридберга, n_i и n_j – целые числа, причем n_j может принимать значения (n_i + 1),(n_i + 2),(n_i + 3),....

Рассмотрим переход атома из различных возбужденных состояний на один и тот же энергетический уровень, определяемый квантовым числом n_i. Совокупность спектральных линий, отвечающая таким переходам, образует серию. Таким образом, n_i определяет серию. Соответственно квантовое число n_j определяет энергетический уровень, с которого имел место данный переход, то есть линию в серии.

Различным сериям атома водорода: Лаймана, Бальмера, Пашена, Брэккета, Пфунда отвечают соответственно значения n_i = 1, 2, 3, 4, 5.

Рассмотрим, как определить частоты спектральных линий атома водорода, принадлежащих серии Бальмера, используя комбинационный принцип, математическое выражение которого представлено равенством (2). Для серии Бальмера n_i = 2, n_j = 3, 4, 5... Следовательно,

ν = Rc 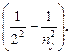(5)

 

Если приписать n_j значения соответственно 3, 4, 5, 6, то из уравнения (5) получим значения частот спектральных линий, лежащих в видимой области и обозначаемых в спектроскопии H _a H _b H_γ, H _d. По мере увеличения n_j разность частот соседних линий уменьшается, и при n_j → ¥ сами частоты стремятся к пределу

n_ГР = R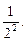

где n_ГР– частота, соответствующая границе серии Бальмера. У каждой серии есть своя граница, соответствующая ей частота определяется соотношением:

n_ГР = R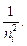

Рассмотрим физический смысл n_ГР. Согласно Бору, при переходе атома с более высокого j -го энергетического уровня на менее высокий i -й уровень излучается квант энергии

 

hν = E_j - E_i (6)

 

Соответственно, чтобы перевести электрон с уровня i на уровень j, необходимо сообщить ему такую же энергию.

Частота ν_гропределяет энергию (Е = h n_ГР), которую надо сообщить электрону, чтобы удалить его с уровня, определяемого числом и, в пространство за пределы атома, где его полная энергия должна быть равна нулю.

Описанный процесс называется процессом ионизации, а Е = h n_ГР является энергией ионизации атома в данном состоянии.

Эта величина связана с потенциалом ионизации простым соотношением: j = h n_ГР/ e, где e – элементарный заряд, равный 1,6×10^-19 Кл.

Процесс обратный ионизации: захват электрона атомом будет сопровождаться излучением света.

Поскольку электрон, отделенный от атома, может обладать произвольной кинетической энергией W _К, то при его захвате ионом должна освобождаться энергия (h n_ГР + W _К).Следовательно, согласно второму постулату Бора (1) в этом случае будет испускаться электромагнитное излучение с частотой

 

ν = 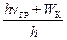= n_ГР +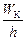

 

Таким образом, возможно излучение с частотой, большей нежели частота границы серии, на любую величину W _К/ h. Это означает, что к границе серии со стороны высоких частот прилегает сплошной спектр. Излучение спектров испускания позволяет исследовать строение атома.

 

Приборы и оборудование

 

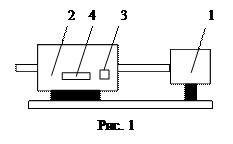
Схема установки приведена на рис. 1. Установка содержит излучатель 1 и монохроматор 2. Блок излучателя содержит лампу ТВС-15, заполненную водородом, устройство ее питания и кодиро

вочный узел.

 

Монохроматор предназначен для выделения и исследования монохроматического излучения в спектральном диапазоне от 2000 до 8000 ангстрем. Для наблюдения спектра на выходной патрубок надевается окуляр, положение которого регулируется наблюдателем. Сканирование спектра осуществляется вращением ручки 3 рядом с индикатором цифрового счетчика длин волн 4. Первые три цифры счетчика 4 соответствуют длине волны в нм, по барабану с рисками отсчитываются десятые доли нм в том же окне.

 

Внимание! Перед включением необходимо проверить заземление излучателя.

 

Порядок выполнения работы

 

1. Провести начальную юстировку системы на оптической скамье по схеме на рис. 1 Вертикальная юстировка осуществляется перемещением держателя в рейтере, горизонтальная позволяет перемещать центр области свечения лампы относительно оси излучателя по горизонтали от 0 до 3 мм для лучшего совмещения с выходным окном излучателя.

 

2. Установить щель и окуляр монохроматора.

 

3. Ручкой монохроматора установить какую-либо линию спектра и провести окончательную юстировку системы, используя юстировочную ручку излучателя.

 

4. Просканировать весь наблюдаемый спектр. Видеть спектральные линии можно с помощью окуляра. Измерения провести два раза и усреднить. Результаты измерений занести в таблицу

Таблица

Цвет линии	ni	nj	l	lСР	R ´
Красная
Голубая
Фиолетовая

 

6. Построить график зависимости 1/λ от разности 1/ n _i² - 1/ n _j² и оценить постоянную R как численно равную тангенсу угла наклона прямой на графике к оси абсцисс.

Оценить точность измерения, сравнив экспериментально найденное R _СР с теоретическим (R _ТЕОР = 3,29×10¹⁵ c^-1). Относительную ошибку определить по формуле:

 

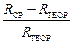×100 %.

 

Контрольные вопросы

1. Сформулируйте постулаты Бора.

2. Рассчитайте по теории Бора радиус первой орбиты атома водорода.

3. Рассчитайте энергию атома водорода по теории Бора в основном состоянии (n = 1).

4. Что определяют в формуле (4) квантовые числа n_i и n_j?

5. Объясните закономерности в спектре атома водорода.

6. Что называется серией?

7. Что такое граница серии?

8. Что называется потенциалом ионизации? Как он определяется?

 

 

Список литературы

 

1. Курс физики: Учеб. пособие для студ. вузов. / А.А. Детлаф, Б.М. Яворский. 7-е изд., стер. – М.: Издат. центр «Академия», 2008. – 720 с.

2. Курс физики: Учеб. для вузов / Т.И. Трофимова. – 7-е изд., стер. – М.: Высшая шк., 2003. – 542 с.

3. Курс общей физики. Кн. 5. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц: Учеб. пособие для втузов. / И.В.Савельев. – М.: ООО «Издательство Астрель». – 2002. – 368 с.