ТЕМА: Статистические показатели
Статистический показатель - это обобщающая характеристика какого-то свойства совокупности, группы; этим он отличается от индивидуальных значений, которые называются признаками.
Показатели свойств конкретных объектов включают: экономические показатели (себестоимость продукции отраслей, предприятий и т.д.); демографические (показатели рождаемости); макроэкономические (характеризуют особенности страны ВВП, НД); показатели обеспеченности населения товарами и услугами и т.д. Эти показатели не являются продуктом самой статистики.
Показатели статистических свойств любых массовых явлений не зависят от конкретного содержания этих явлений (показатели динамики, вариации и т.д.).
Абсолютным показателем является показатель, отражающий либо суммарное число единиц, либо суммарное свойство объекта.
Относительным показателем является показатель, полученный путем сравнения, сопоставления абсолютных или относительных показателей в пространстве (т.е. между объектами), во времени (по одному и тому же объекту), или в результате сравнения показателей разных свойств изучаемого объекта.
Различают следующие группы относительных показателей:
- о тносительные величины структуры рассчитываются как отношение части к целому;
- о тносительные величины динамики рассчитываются, как отношение показателей, характеризующих объект в более поздний (текущий) период к аналогичным показателям того же объекта в более ранний (базисный) период;
- о тносительные величины координации отражают отношение численности двух частей единого целого (сколько служащих приходится на 100 рабочих);
- относительные величины интенсивности представляют результат сопоставления двух разноименных статистических показателей (потребление мяса на душу населения);
- относительные величины наглядности строятся как результат сравнения разных объектов по одинаковым признакам (сравнение годовой производительности труда по двум предприятиям);
- относительные величины выполнения плана или относительные величины планового задания рассчитываются как отношение фактически наблюдаемых величин признака к его нормативным, плановым, оптимальным или максимально возможным величинам.
ТЕМА: Средние величины и Вариационный анализ
Вариацией значений какого-либо признака совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени. Вариации значений присуще всем явлениям природы и общества, она является предметом изучения статистики. Большинство методов статистики либо метод изучения вариаций, либо метод абстрагирования от нее.
Этапы изучения вариации
1) построение вариационного ряда;
2) графическое изображение вариационного ряда, анализ графического изображения;
3) анализ вариационного ряда с помощью системы показателей.
Для анализа вариационного ряда используем трои группы показателей.
1 группа - показатели центра распределения (мода, медиана, средняя арифметическая)
2 группа- показатели степени вариаций (для оценки размера и интенсивности вариаций)
3 группа - показатели формы распределения
Медиана – это величина варьирующего признака, делящая совокупность на две равные части: со значениями признака меньше медианы и больше медианы.
Способы нахождения медианы
1) Графически (кумулята);
2) в ранжированном вар. ряду с нечетным числом членов медианой является значение признака у средней в ряду единицы;
3) в дискр. вар. ряду – значение признака в той группе, в которой накопленная частота превышает половину численности совокупности;
4) 
по формуле.
, где
Me – медиана;
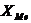- нижняя граница медианного интервала (интервала для которого накопленная частота впервые превысит полусумму частот)
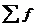- сумма частот ряда
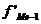- сумма накопленных частот предшествующих медианному интервалу
- частота медианного интервала.
Аналогично медиане определяется квартили - это значения признака, делящие совокупность на четыре равные по числу единиц части. 2-й квартиль равен Ме.
Мода - это величина варьирующегося признака, которые встречаются в изучаемом ряду чаще всего. Графически мода может быть определена по гистограмме.
Модальным является интервал с максимальной частотой. Мода может быть определена по формуле:
, где
Mo – мода;
Xmo - нижняя граница модальности (интервал ряда с наибольшей частотой);
fMo - частота модального интервала;
fMo-1 - частота интервала предшествующего модальному;
fMo+1 - частота интервала следующего за модальным.
Мода дискретного вариационного ряда - это значение признаков с максимальной частотой.
Средней арифметической величиной называется такое среднее значение признаков при вычислении которого общий объем признаков совокупности сохраняется неизменным.
Простая средняя арифметическая используется для не сгруппированных данных:
, где
- средняя величина;
n - численность совокупности.
Взвешенная средняя арифметическая используется для сгруппированных данных:
- численность (частоты);
- сумма частот.
Показатели, используемые для оценки размера и интенсивности вариации
1) абсолютные: размах (амплитуда) вариации, среднее линейное отклонение, СКО, дисперсия, среднее квартильное расстояние;
2) относительные: отн. размах вариации, относительное линейное отклонение, коэффициент вариации (отн. квадратичное отклонение), относительное квартильное расстояние
Абсолютные:
1. Размах или амплитуда вариаций, определяется как разница между максимальным и минимальным значением признака в совокупности:
R=Xmax-Xmin.
2. Среднее линейное отклонение, определяется как сумма индивидуальных значений признаков:
- простая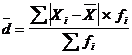 
-взвешенная
3. Среднее квадратическое отклонение рассчитывается как корень из среднего квадрата разности:
Квадрат среднего квадрата отклонения равен дисперсии.
4.Дисперсия:
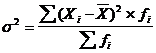
Относительные показатели вариации строятся как отношение значения соответствующего абсолютного показателя к средней величине признака по совокупности.
1. Относительный размах вариаций:
2. Относительное линейное отклонение:
- Относительный квадратическое отклонение или коэффициент вариаций:
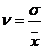*100%
Совокупность считается однородной, если коэффициент вариаций не превышает 33 %.
ТЕМА: Статистическое изучение и моделирование динамики –
Ряд динамики – это числовые значения (уровни статистического показателя) представленные во временной последовательности. Ряды динамики представляются в виде таблицы, состоящей из двух строк или граф.
Интервальный динамический ряд - ряд динамики, в котором время задано в виде промежутков (прибыль предприятия по годам).
Моментальный динамический ряд - ряд динамики, в котором время задано в виде конкретных дат (численность населения)
Задачи, возникающие при изучении рядов динамики:
1) охарактеризовать интенсивность развития явления от периода к периоду (от даты к дате);
2) охарактеризовать среднюю интенсивность за исследуемый период;
3) выявить основную тенденцию в развитии явления;
4) осуществить прогноз развития на будущее;
5) изучить сезонные колебания.
Для характеристики интенсивности развития явления от периода к периоду (от даты к дате) используются следующие показатели динамики:
1) абсолютные приросты (характеризуют абсолютное изменение уровня признака по сравнению с принятым за базу сравнения):
| Цепная форма | Базисная форма |
| 
|
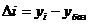
2) коэффициент роста показывает во сколько раз уровень сравниваемого периода больше уровня принятого за базу сравнения:
| Цепная форма | Базисная форма |
| 
|
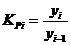
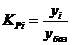
3) темп роста - отношение уровня текущего периода к базисному, выражается в процентах. Говорит о том, сколько процентов составляет уровень сравниваемого периода от уровня базового периода.
4) темп прироста показывает на сколько процентов уровень текущего периода превышает уровень периода, принятого за базу сравнения:
5) абсолютное значение 1% прироста - одна сотая часть абсолютного прироста. Рассчитывается только если абсолютный прирост - положительная величина.
Средняя интенсивность развития явления за весь период характеризуется с помощью средних показателей динамики:
1) средний уровень ряда
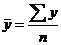
2) средний абсолютный прирост
3) средний коэффициент роста
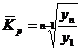
4) средний темп роста
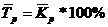
5) средний темп прироста
Коэффициент опережения используется при анализе взаимосвязанных рядов динамики; показывает, во сколько раз 1 ряд динамики растет быстрее другого.
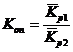
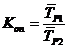
Существует два основных способа выявления основной тенденции развития:
1) механическое выравнивание (переменные и скользящие средние),
2) аналитическое выравнивание (построение уравнения тренда).
Методы механического выравнивания:
- трехчленная переменная средняя:
; 
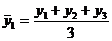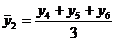
- трехчленная скользящая средняя:
; 
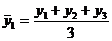Скользящая средняя - подвижная динамическая средняя, которая вычисляется по ряду при последовательном передвижении на один интервал.
Аналитическое выравнивание используется для описания плавной линии развития (тренда ряда). Сущность аналитического выравнивания заключается в нахождении уравнения, выражающего закономерность развития явления как функцию времени y=f(t).
Для вычисления коэффициентов уравнения по уравням динамического ряда используется метод наименьших квадратов ( МНК).
Для нахождения коэффициентов уравнения прямой
используется следующая система нормальных уравнений:
Для определения коэффициентов параболы вида 
решается следующая система нормальных уравнений:
; 
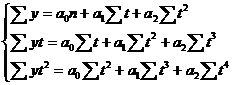Для оценки качества уравнения рассчитывается ошибка аппроксимации:
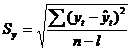
-значение по уравнению, модельное;
- число параметров уравнения;
- число уровней ряда.
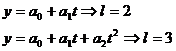
Методика изучения дисциплины «статистика» студентами заочной формы обучения
2012/2013 уч. год, доц. Петрова В.В.
Теоретические вопросы в соответствии с нижеприведенным списком изучаются студентами самостоятельно. Аудиторные занятия реализуются в форме выполнения типовых расчетов по ряду тем в MS Excel (под руководством преподавателя) с последующей интерпретацией результатов. Изучение материала закрепляется в ходе самостоятельного выполнения курсовой или контрольной работы.
Вопросы для проведения экзамена
по курсу “статистика”
Тема 1. Предмет и метод статистики. Задачи, организация
1. Назовите и определите 3 смысла слова “статистика”
2. Почему статистика изучает совокупности явлений, а не единичные явления?
3. Что такое статистические закономерности? Чем они отличаются от динамических?
4. Что такое “закон больших чисел” применительно к статистическим закономерностям?
5. Перечислите виды измерителей в статистике, приведите по 1 примеру
6. Что такое единица совокупности?
7. Что такое статистические совокупности?
8. Что является предметом статистического изучения?
9. Классификация признаков в статистике: основания классификации, названия и определения классов, примеры признаков разных классов
10. Представьте схематично метод статистики
11. Что такое статистический показатель?
12. Чем отличается статистический показатель от признака? Приведите пример.
13. Классификация видов статистических показателей: основания классификации, названия и определения классов, примеры
Тема 2. Статистическое наблюдение
14. Что такое статистическое наблюдение?
15. Классификация видов статистического наблюдения: основания классификации, названия и определения классов, примеры
16. Что такое статистическая отчетность?
17. Назовите виды ошибок, возникающих при статистическом наблюдении
18. Назовите причины использования выборочного метода
19. Каким образом формируется простая случайная выборка? Повторная и бесповторная выборка.
20. Каким образом реализуется механическая выборка? Что определяют при ее организации?
21. Какие выборки называют малыми?
Тема 3. Статистическая группировка, сводка и способы представления данных
22. Что такое статистическая группировка?
23. Определите виды статистических группировок, приведите примеры
24. Что такое закрытые и открытые интервалы?
25. Запишите формулу для нахождения величины равного интервала
Тема 4. Средние величины и вариационный анализ
26. Какими свойствами обладают все массовые явления и процессы?
27. Что такое вариация?
28. В чем заключается главное значение средних величин?
29. Дайте определение средней арифметической величины.
30. Запишите формулу простой средней арифметической
31. Запишите формулу взвешенной средней арифметической
32. Перечислите категории средних величин и виды средних, которые к ним относятся
33. Запишите формулу степенной средней степени k
34. Запишите формулу средней квадратической. Какой статистический показатель строится на ее основе?
35. Запишите формулу средней кубической величины
36. Запишите формулу средней геометрической. Какой статистический показатель строится на ее основе?
37. В чем заключается правило мажорантности средних?
38. Что такое средняя величина?
39. Что такое ряд распределения?
40. Назовите формы вариационного ряда, дайте определения
41. Что такое частота (при построении вариационного ряда)?
42. Что показывает накопленная частота, как она рассчитывается?
43. Что такое частость?
44. Перечислите, определите и изобразите виды графического изображения вариационного ряда. Что показывает каждый из графиков?
45. Перечислите этапы изучения вариации
46. Что такое медиана? Опишите способы ее нахождения (без формул)
47. Что такое мода? Графический способ ее определения. Какой интервал является модальным? Мода дискретного вариационного ряда
48. Что такое размах (амплитуда) вариации?
49. Перечислите показатели, используемые для оценки размера и интенсивности вариации. Запишите формулы любых трех показателей из их числа
50. Как рассчитывается среднее линейное отклонение?
51. Понятие дисперсии, формула расчета
52. По какому принципу строятся относительные показатели вариации?
53. Как рассчитывается коэффициент вариации?
Тема 5. Статистическое изучение динамики
54. Что такое ряд динамики?
55. Перечислите виды рядов динамики. Определите каждый вид.
56. Какие задачи встают перед статистикой при изучении рядов динамики?
57. Какие показатели используются для характеристики интенсивность развития явления от периода к периоду?
58. Как рассчитывается абсолютный прирост?
59. Как рассчитывается абсолютное ускорение?
60. Что такое коэффициент роста? О чем говорит его значение?
61. Что такое темп роста? О чем говорит его значение?
62. Что такое темп прироста?
63. Что такое тренд?
64. Перечислите показатели, с помощью которых можно охарактеризовать среднюю интенсивность развития явления за исследуемый период
65. Что такое переменная средняя и для чего она используется?
66. Что такое скользящая средняя и для чего она используется?
67. Что такое интерполяция?
68. Что такое экстраполяция?
69. На основе годовых данных об изменении урожайности картофеля (ц/га) в регионе с 1989г. по 1998г. (t=1,2,...,10) были оценены коэффициенты линейного тренда: У=180,5+5,1*t. Чему равен среднегодовой прирост урожайности?
70. См. вопрос № 66: чему равен прогноз урожайности картофеля в регионе на 1999г.?
71. Что характеризуют точечный и интервальный прогнозы?
Тема 6. Корреляционно-регрессионный анализ
72. Перечислите основные виды связей. Определите каждый вид
73. Какая связь называется функциональной?
74. Какая связь называется статистической?
75. Какая связь называется корреляционной?
76. Что такое корреляционный анализ?
77. Что такое регрессионный анализ?
78. С помощью какого метода оцениваются параметры уравнения регрессии? В чем его сущность?
79. Алгоритм изучения парной корреляционной связи
80. Что такое парная корреляция?
81. Что такое множественная корреляция?
82. Что значит прямая связь? Обратная связь?
83. Каким образом определяется степень тесноты парной зависимости? Показатели, интерпретация значений.
84. Линейный коэффициент корреляции равен 1. Что можно сказать о характере связи?
85. Линейный коэффициент корреляции равен -1. Что можно сказать о характере связи?
86. Линейный коэффициент корреляции равен 0. Что можно сказать о характере связи?
87. С помощью каких показателей оценивается статистическая значимость коэффициентов уравнения регрессии? Опишите принцип их использования
88. Фактическое значение t-статистики по модулю меньше табличного. Что можно сказать о коэффициенте уравнения регрессии?
89. Фактическое значение F-критерия больше табличного. Что можно сказать об уравнении регрессии?
90. Коэффициент детерминации равен 0,87. Что можно сказать о соответствующем уравнении регрессии?
91. Для чего используются коэффициент детерминации, F-критерий Фишера, t-статистика Стьюдента, парный и множественный коэффициенты корреляции, ошибка и коэффициент аппроксимации. Интерпретация значений, алгоритм использования
92. Зависимость потребления мяса (кг/на члена семьи) от дохода на члена семьи (тыс.руб) описывается уравнением y=2+0,12x. Какой вывод можно сделать по этому уравнению?
Основная литература
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. чл. – корр. РАН И.И. Елисеевой. – М.: Финансы и статистика, 1998.
2. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учеб. пособие. - М.: Финансы и статистика, 2001. – 208 с.
3. Статистика рынка товаров и услуг: Учебник. – 2-е изд.. / Под ред. проф. И.К. Беляевского. – М.: Финансы и статистика, 2002. – 656 с.
4. Статистика финансов: Учебник. – 2-е изд. / Под ред. проф. В.Н. Салина. – М.: Финансы и статистика, 2002. – 816 с.
Дополнительная литература
5. Рябушкин Б.Т. Национальные счета и экономические балансы: практикум: Учеб. пособие. – 2-е изд. - М.: Финансы и статистика, 2002. – 256 с.
6. Экономическая статистика: Учебник. - 2-е изд. / Под ред. проф. Ю.Н. Иванова. – М.: ИНФРА-М, 2001. – 480 с.