Вариант 8.
Решить задачу, используя диаграмму Эйлера-Венна.
В одной из студентческих групп все студенты умеют программировать. Десять человек умеют работать на Бейсеке. 10 на Паскале, 6 на Си. Два языка знают: 6 человек Бейсик и Паскаль, 4 – Паскаль и Си, 3 – Бейсик и Си. Один человек знает все три языка. Сколько студентов в группе?
Решение:
В задаче идет речь о следующих множествах:
U - – множество студентов в группе;
А – множество студентов умеющие работать на Бейсик;
В – множество студентов умеющие работать на Паскаль;
С – множество студентов умеющие работать на Си.
По условию задачи:
10 человек умеют работать на Бейсик т.е.  ;
;
10 человек умеют работать на Паскаль, т.е. 
6 человек умеют работать на Си, т.е.  ;
;
6 человек умеют работать на Бейсик и Паскаль, т.е.  ;
;
4 человека умеют работать на Паскаль и Си, т.е.  ;
;
3 человека умеют работать на Бейсик и Си, т.е. 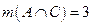 ;
;
1 человек умеет работать на всех трех языках, т.е.  .
.
Требуется найти число число студентов в группе, т.е.  .
.
Перенесем эти данные на диаграмму Эйлера-Венна.

Тогда  .
.
Ответ: 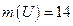 .
.
2. Задано универсальное множество  и множества
и множества  ,
, 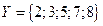 ,
,  . Записать булеан множества X, любое разбиение множества Y, покрытие множества Z. Выполнить действия
. Записать булеан множества X, любое разбиение множества Y, покрытие множества Z. Выполнить действия  .
.
Решение:
Для нахождения множества  выполним операции над множествами в следующем порядке:
выполним операции над множествами в следующем порядке:
1) 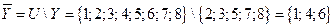 - по определению операции отрицания; 2)
- по определению операции отрицания; 2)  - по определению операции дополнения;
- по определению операции дополнения;
3) 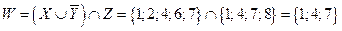 - по определению операции пересечения.
- по определению операции пересечения.
Итак, 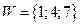 .
.
Для построения булеана множества X воспользуемся двоичной записью числа.
Т.к. множество Х содержит 5 элементов, то его булеан содержит 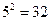 подмножеств. Будем записывать номер подмножества пятиразрядным двоичным числом от 0 до 31, включая в подмножество только те элементы, которым соответствует единица в двоичном разряде. Результаты внесем в таблицу:
подмножеств. Будем записывать номер подмножества пятиразрядным двоичным числом от 0 до 31, включая в подмножество только те элементы, которым соответствует единица в двоичном разряде. Результаты внесем в таблицу:
| № подмножества | Двоичная запись номера | Подмножества множества 
| № подмножества | Двоичная запись номера | Подмножества множества 
|

| 
| ||||

| 
| ||||

| 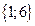
| ||||

| 
| ||||
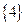
| 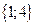
| ||||

| 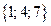
| ||||
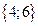
| 
| ||||
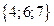
| 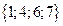
| ||||
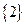
| 
| ||||
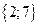
| 
| ||||

| 
| ||||

| 
| ||||

| 
| ||||

| 
| ||||

| 
| ||||

| 
|
Итак, в булеан множества Х включаем пустое множество, само множество Х, все одноэлементные подмножества, все двухэлементные подмножества множества Х, все трехэлементные подмножества множества Х, все четырехэлементные подмножества множества Х:
B(X)=  ;
;  ;
; 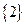 ;
;  ;
;  ;
; 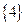 ;
;  ;
;  ;
; 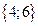 ;
; 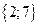 ;
;  ;
;  ;
;  ;
; 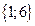 ;
; 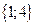 ;
;  ;
; 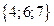 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 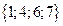 ;
;  ;
;  ;
;  ;
; 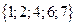 .
.
Для множества Y построим разбиение, состоящее из трех блоков  например, таким образом:
например, таким образом:
 .
.
Определение разбиения выполняется: множества  не пусты, не пересекаются
не пусты, не пересекаются 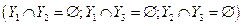 , их объединение равно множеству Y:
, их объединение равно множеству Y:  .
.
Для построения покрытия выберем подмножества  и
и  . Полученная система множеств
. Полученная система множеств  состоит из двух блоков, объединение которых равно множеству Z:
состоит из двух блоков, объединение которых равно множеству Z: 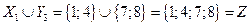 .
.
3. Упростить, используя законы и тождества алгебры множеств (перечислить используемые законы):  .
.
Решение:
Будем считать операция пересечения имеет более высокий приоритет, чем объединение множеств.
Пользуясь этим правилом, определим порядок действий.

1) По закону дистрибутивности:
 .
.
2) По закону ассоциативности:
 .
.
3) По свойству пустого множества:
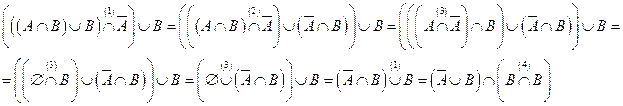
4) По закону идемпотентности:

Ответ:  .
.
4. Пользуясь только определениями операций над множествами и определением равенства множеств, доказать  .
.
Решение:
Пусть  и
и  .
.
По определению равенства множеств покажем, что  и
и 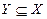 , т.е.
, т.е.  .
.
Пусть  , т.е. по определению объединения и пересечения множеств имеем:
, т.е. по определению объединения и пересечения множеств имеем:
 , т.е.
, т.е. 
Пусть  , т.е. по определению объединения и пересечения множеств имеем:
, т.е. по определению объединения и пересечения множеств имеем:
 , т.е.
, т.е. 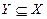 .
.
Т.к.  и
и 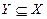 , то
, то  , т.е.
, т.е. 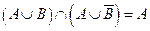 . Ч.т.д.
. Ч.т.д.
5. Пусть  . Отношение
. Отношение 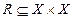 задано характеристическим свойством:
задано характеристическим свойством:

Задать отношение другими возможными способами. Выяснить, какими свойствами оно обладает.
Решение:
Отношение R можно задать перечислением всех элементов:
 .
.
Область определения отношение R:  ;
;
Область значений отношение R:  .
.
Наглядно представить отношение R можно с помощью графика:

С помощью схемы:
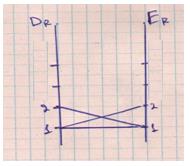
С помощью графа:

С помощью матрицы отношения:
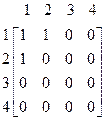
Выясним, какими свойствами обладает отношение.
Рефлексивность.
При  условие
условие  - не выполняется
- не выполняется  - т.е. отношение R не является рефлексивным;
- т.е. отношение R не является рефлексивным; 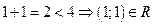 и не является антирефлексивным.
и не является антирефлексивным.
Симметричность.
Пусть  . Составим пару
. Составим пару  и для нее проверим характеристическое свойство отношения:
и для нее проверим характеристическое свойство отношения:  выполняется. Т.е. отношение
выполняется. Т.е. отношение 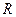 - симметрично.
- симметрично.
Транзитивность: пусть  и
и  , т.е.
, т.е.  и
и  выясним выполняется ли неравенство
выясним выполняется ли неравенство  .
.

 . Т.е. отношение
. Т.е. отношение 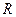 - транзитивно.
- транзитивно.
Отношение R обладает свойствами симметричности и транзитивности, следовательно, не является отношением эквивалентности.
6. Дано множество  и отношение
и отношение  . Показать, что отношение R является отношением порядка. Построить диаграмму Хассе частично упорядоченного множества
. Показать, что отношение R является отношением порядка. Построить диаграмму Хассе частично упорядоченного множества  . Существует ли в множестве X наибольший и наименьший элементы? Существуют ли несравнимые элементы?
. Существует ли в множестве X наибольший и наименьший элементы? Существуют ли несравнимые элементы?
Решение:
Покажем, что отношение R рефлексивно, антисимметрично и транзитивно. Рефлексивность имеет место, так как любое число является своим делителем, т.е. 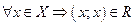 .
.
Пусть одновременно выполняются условия: 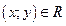 и
и  . Тогда
. Тогда  . Действительно,
. Действительно,  означает, что
означает, что  – делитель
– делитель  , т.е. найдется целое число
, т.е. найдется целое число  такое, что
такое, что  . Одновременно найдется целое число
. Одновременно найдется целое число  такое, что
такое, что 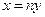 . Отсюда
. Отсюда 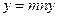 и
и  . Последнее равенство выполняется при
. Последнее равенство выполняется при  или
или 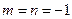 , но все элементы множества X – положительные числа, и второй случай невозможен. Следовательно,
, но все элементы множества X – положительные числа, и второй случай невозможен. Следовательно,  , т.е.
, т.е.  , и отношение R антисимметрично.
, и отношение R антисимметрично.
Пусть  и
и  , значит, найдутся
, значит, найдутся 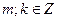 такие, что
такие, что  ,
,  . Тогда
. Тогда  , где
, где  . Следовательно,
. Следовательно,  является делителем
является делителем  и
и  . Отношение R транзитивно.
. Отношение R транзитивно.
Отношение R рефлексивно, антисимметрично и транзитивно, т.е. является отношением порядка. Построим диаграмму Хассе частично упорядоченного множества  . На первом уровне диаграммы поместим элементы
. На первом уровне диаграммы поместим элементы  не имеющие других делителей, кроме себя (
не имеющие других делителей, кроме себя ( и
и  ). На втором уровне – элементы
). На втором уровне – элементы  , не имеющие других делителей, кроме себя и элементов нижнего уровня
, не имеющие других делителей, кроме себя и элементов нижнего уровня  . На третьем уровне – элементы
. На третьем уровне – элементы  , не имеющие других делителей, кроме себя и элементов второго и первого уровня
, не имеющие других делителей, кроме себя и элементов второго и первого уровня 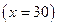 . Соединяем отрезком элементы соседних уровней, если элемент нижнего уровня является делителем элемента соседнего верхнего уровня.
. Соединяем отрезком элементы соседних уровней, если элемент нижнего уровня является делителем элемента соседнего верхнего уровня.

Диаграмма Хассе построена.
Пара элементов  тогда и только тогда, когда двигаясь по диаграмме только вверх, мы можем пройти от элемента
тогда и только тогда, когда двигаясь по диаграмме только вверх, мы можем пройти от элемента  до элемента
до элемента  . По диаграмме Хассе легко обнаружить несравнимые элементы: 3 и 5. Наибольшим элементом является
. По диаграмме Хассе легко обнаружить несравнимые элементы: 3 и 5. Наибольшим элементом является 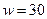 (для всех
(для всех  выполнено условие «
выполнено условие «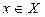 является делителем 30»). Наименьшего элемента нет, но есть два минимальных
является делителем 30»). Наименьшего элемента нет, но есть два минимальных  и
и  .
.
7. Заданы отношения 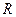 и
и  :
:


| 
|

| 
|
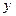
| 
|

| 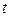
|


| 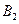
| 
|

| 
| 
|

| 
| 
|

| 
| 
|
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция отношения S на список (2,1);
б) соединение отношений R и S по условию «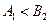 ».
».
Решение:
Степень отношения 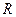 равна 2;
равна 2;
Степень отношения  равна 3.
равна 3.
Т.к. степень отношений 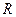 и
и  различны, то отношения
различны, то отношения 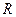 и
и  - несовместимы и над ними нельзя выполнить операции пересечения, объединения и разности.
- несовместимы и над ними нельзя выполнить операции пересечения, объединения и разности.
a) 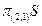 - проекция отношения
- проекция отношения  на список
на список  .
.
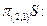

| 
|

| 
|

| 
|

| 
|
Одинаковых строк нет.
б) соединение отношений R и S по условию «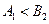 ».
».

| 
| 
| 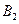
| 
|

| 
| 
| 
| 
|
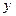
| 
| 
| 
| 
|

| 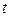
| 
| 
| 
|

| 
| 
| 
| 
|
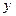
| 
| 
| 
| 
|

| 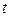
| 
| 
| 
|

| 
| 
| 
| 
|
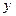
| 
| 
| 
| 
|

| 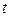
| 
| 
| 
|

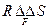
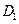
| 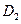
| 
| 
| 
|

| 
| 
| 
| 
|
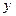
| 
| 
| 
| 
|

| 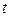
| 
| 
| 
|

| 
| 
| 
| 
|
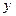
| 
| 
| 
| 
|

| 
| 
| 
| 
|
8. Даны множества  и
и  . Какова мощность множеств
. Какова мощность множеств  ,
, 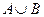 ,
,  ?
?
Решение:
Множество A конечно и задано перечислением своих элементов, множество B задано характеристическим свойством. Запишем несколько первых элементов множества  .
.
 , тогда мощности
, тогда мощности  равна единице:
равна единице:  , т.е. множество
, т.е. множество  конечно.
конечно.
Покажем, что множество  счетно. Занумеруем его элементы:
счетно. Занумеруем его элементы:
 .
.
Задана биекция множества  на множество
на множество  , следовательно,
, следовательно,  счетно и
счетно и  .
.
По определению декартова произведения  . Запишем элементы этого множества в виде матрицы и занумеруем их по столбцам.
. Запишем элементы этого множества в виде матрицы и занумеруем их по столбцам.

| … | ||||

| 
| 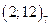
| 
| … | |
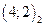
| 
| 
| 
| … | |

| 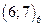
| 
| 
| … |
Замечаем, что если номер  делится на 3 без остатка, то первый элемент пары равен 6; если номер
делится на 3 без остатка, то первый элемент пары равен 6; если номер  делится на 3 с остатком 1, то первый элемент пары равен 4; если номер
делится на 3 с остатком 1, то первый элемент пары равен 4; если номер  делится на 3 с остатком 2, то первый элемент пары равен 2. Поэтому способ нумерации может быть задан следующим образом:
делится на 3 с остатком 2, то первый элемент пары равен 2. Поэтому способ нумерации может быть задан следующим образом:

и множество  счетно, т.е. имеет мощность
счетно, т.е. имеет мощность  .
.
9. Равномощны ли множества 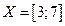 и
и  ?
?
Решение:
Покажем, что множества равномощны по теореме Кантора–Бернштейна, т.е. покажем, что найдется 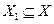 такое, что
такое, что  равномощно
равномощно  , и найдется
, и найдется  такое, что
такое, что 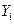 равномощно X.
равномощно X.
Пусть 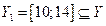 . Установим биекцию
. Установим биекцию 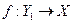 следующим образом:
следующим образом: 
Множества  и
и  равномощны.
равномощны.
Пусть  . Установим биекцию
. Установим биекцию  следующим образом:
следующим образом:  .
.
Множества  и
и 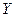 равномощны.
равномощны.
По теореме Кантора–Бернштейна  .
.