Фрагмент урока
Предмет: математика
Учебник: Моро 1 класс, часть2
Тема урока: «Объём. Единицы объёма.».
Цель: формирование математического понятийного аппарата учащихся через ознакомление с новой величиной – объёмом.
Задачи урока:
1)Повторение изученного материала
2) Познакомить с различными приёмами сравнения площади;
3) Использование приемов сравнения площадей сочетанием разных форм организации работы: фронтальной, групповой, индивидуальной.
4) Закрепление изученного материала
С этой величиной детей знакомят по-разному в разных программах. Так по программе М.И. Моро термин объём не вводят, а используют понятие «ёмкость сосуда».
-Ребята, сегодня мы с вами познакомимся с Ёмкостью сосудов.
Ёмкость- это то, сколько помещается какого-либо вещества в сосуд.
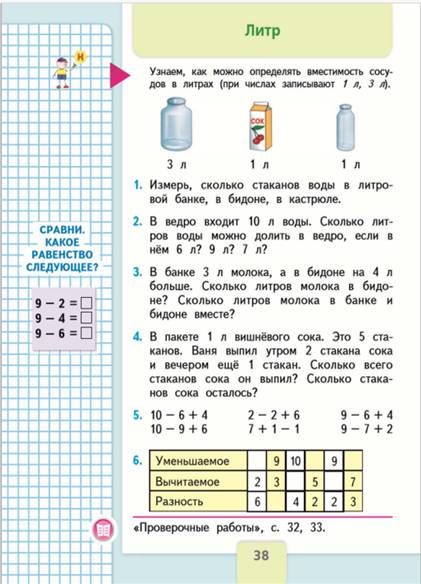
Давайте проверим, сколько стаканов воды помещает в трёхлитровой банке.
Сейчас я возьму стаканы с водой и буду по очереди их наливать в банку, а вы вместе со мной будете считать.
В банке поместилось 10 стаканов воды.
Теперь проверим, сколько в литровую банку поместится стаканов воды.
Итак, в литровой банке- 5 стаканов воды.
А теперь вы возьмете кастрюлю и проверите, сколько же поместилось в нее стакан воды. (Ответы у всех разные, так как кастрюли детки принесли все свои)
Какие задания целесообразно предложить учащимся с целью формирования у них представления об объеме как свойстве трехмерной фигуры? Какие задания из различных учебников математики можно использовать для этого?
Чтобы помочь детям выделить массу среди других свойств следует предлагать им для сравнения предметы, имеющие одинаковую форму, но разные массы, одинаковую форму и размеры, но равные массы и т.д. Сюда следует включать и цвет, и материал, из которых сделаны предметы, и добиваться, чтобы дети различали размеры, форму, массу.
Так как в начальных классах не вводится понятие объема и не изучаются единицы измерения объема, то следует ограничиться ознакомлением учащихся с процессом измерения вместимости некоторых предметов (банка, кастрюля, металлическая кружка, стакан). Целесообразно показать сравнение емкостей, выявить, какая из них больше и показать необходимость использования единой меры - литра.
 М1М часть 2
М1М часть 2
 М1Демидова часть 3
М1Демидова часть 3

 М1Петерсон Часть 3
М1Петерсон Часть 3

 М4 Чекин Часть 1
М4 Чекин Часть 1
3. Составьте вариант беседы ознакомления учащихся с понятием «Объём фигуры» при изучении трёхмерных геометрических фигур по программам Н.Б.Истоминой или И.И. Аргинской (М4И ч.2 с.32; М4А ч.2 с.16).
Ребята, как вы думаете все ли величины мы изучили?(нет)
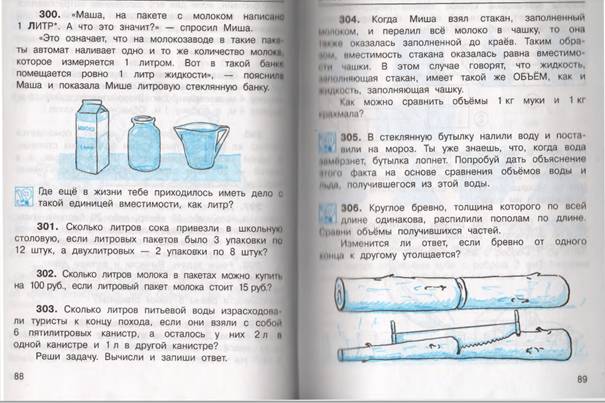
сегодня я вас познакомлю с новой величиной. Откроем с вами учебники. Перед нами 2 отрезка. (Маленький отрезок-это единица длины,т.е см.С ее помощью мы можем измерить длину большего отрезка)
На второй картинке представлены 2 квадрата(Это единица площади – см2.)
Посмотрите на 3 картинку. На ней изображены 2 куба. А кто-нибудь из вас знает, что такое куб? (Это объёмная фигура)
Оказывается,куб-это тоже мерка. Мерка,с помощью которой можно измерять объемы геометрических тел.
Мы с вами можем измерить его площадь, так как у него есть длина и ширина, но, а также можно измерить его объём. Это и будет тема нашего урока.
Вспомним: Для того, чтобы найти квадрат, нужно умножить длину и ширину. А чтобы найти объём, нужно перемножить все его стороны(Длину, ширину и высоту)
С какими единицами измерения объема фигуры знакомят учащихся по этим и другим программам. Какие методические приемы используют для этого? Приведите примеры различных заданий из учебников математики.
Детей знакомят с кубическими сантиметрами, метрами, дециметрами. Анализируя куб и прямоугольный параллелепипед, говорят о единицах измерения объема.


 М3 Демидова Часть1
М3 Демидова Часть1
Опишите методику знакомства учащихся с правилом нахождения объёма куба и прямоугольного параллелепипеда по программе И.И. Аргинской М4А ч.2 с.20 и 26. Составьте фрагмент урока по одной из этих страниц.
По программе Аргинской И.И. выводят правило нахождения объёма куба и прямоугольного параллелепипеда.
V = a ∙b ∙c. Для вывода этого правила рассматриваем модель прямоугольного параллелепипеда. Можно её сложить из кубиков, принимая, что 1 кубик = 1 единице объёма, например 1 дм3.
«Формула объёма прямоугольной призмы выглядит так: V = a ∙b ∙c.
V-объем
a-длина
b-ширина
c-высота»
Ребята, а открываем страницу 26 упражнение 323. На данном рисунке изображён чертёж коробки. Сколько кубиков объёмом 1см3 поместится в этой коробке? (Ответ: 24)
А какое значение произведения длины, ширины и высоты коробки? (Ответ: 24 см3)


Составьте беседу об истории возникновения различных мер емкости сосудов и объема фигур.
Первым письменным упоминанием о мерах, применявшихся на Руси, является Устав князя Владимира, относящийся к 996 году. Устав предписывал: "извесы и мерила блюсти без пакости, ни умалити, ни умножити". Эти первые эталоны измерения мер висели в церквях и продавцы должны были "крест целовать" - давать клятвенное обещание в том, что будут взвешивать товары без обмана.
В Древней Руси, как и во многих других странах, меры объема имели две области применения: для сыпучих тел и для жидкостей.Для мер жидкости чаще всего употреблялись бочка, ведро, корчага. Наибольшее распространение получило ведро, практически очень удобная мера, сохранившаяся до XX века.
В письменных памятниках X-XIII вв. термин «ведро» упоминается в двух значениях: во-первых, как хозяйственный сосуд, и, во-вторых, как единица объема. В значении «сосуд, определенно установленного объема».Причем образцом для измерения объема жидких веществ было ведро дворцовое. Первоначально оно делилось на двенадцать кружек, каждая из которых содержала в себе почти три фунта чистой воды.
Но позже, в 1621 году не была установлена единая московская мера. В настоящее время термин «ведро» сохранил свое древнее значение и продолжает также активно употребляться в быту.
Ещё одной древней и распространённой единицей объёма жидкости у многих народов является бочка. Объем бочки был различным даже в пределах одной местности. Мера объема бочки колеблется от 10 до 40 ведер, причем бочка, содержащая в себе 40 ведер, называлась мерною или чаще сороковой.
Если ведро и бочка известны всем и до сих пор употребляются и как мера, и как тара, то слово «варя» скорее всего, будет для многих уже непонятным. А в Древней Руси варей измеряли что-то очень большого объема, то, что варили в один прием (например, пиво или мед для свадьбы, а свадьба продолжались от трех дней до недели).
Также,чтобы купить,например,полведра крупы люди использовали деление. Деление на два было самым простым и широко применялось в торговле. Такое деление давало меру, равную половине ведра, его четверти и восьмой части ведра. Эта последняя мера, которая помимо названия по соответствующей части ведра (осьмушка), называлась еще кружкой. Это наименование употреблялось чаще. Эта мера объема сохранилась до наших дней. Термин четверть или четвертник, как четвертая часть ведра, известен с XV века и официально употребляется до XVIII века. К наименованиям мер объема жидкостей, определяющих конкретную часть ведра, относится сотка или, чаще используемое в народе название – чарка.
Проходит время, мер измерения объема становится больше и больше. Но потом была подписана единая мера измерения для всех.

