Белый шум не имеет памяти о прошлых событиях - текущие значения параметров процесса не зависят от прошлых значений. Большинство процессов не вырабатывают белого шума вплоть до бесконечной частоты, но их память зачастую ограничена одной постоянной времени или переменной состояния. Шум типа 1/ f — это процесс, имеющий память. Вопрос заключается в том, в какой степени и как долго эти процессы подвержены влиянию своего прошлого? В настоящем разделе мы попытаемся ответить на эти вопросы. С этой целью рассмотрим сначала приближенные функции автокорреляции, полученные в разд. II, чтобы показать, как долго процесс «помнит», а затем рассмотрим еще одну линейную систему, вырабатывающую шум типа 1/ f, чтобы показать, сколько начальных условий «помнит» процесс.
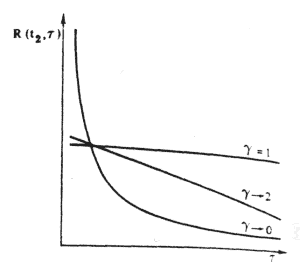
Шум типа 1/ f — это случайный процесс с очень длительной памятью. Полученные выше автокорреляционные функции (рис. 6) спадают во времени по показательному закону - медленнее, чем по экспоненте. В случае когда g в точности равно 1, спад является логарифмическим и происходит медленнее, чем при какой-либо степенной зависимости. Чем ближе g к 1, тем сильнее влияние отдаленного прошлого по сравнению с влиянием недавнего прошлого. Когда g=1, текущие события примерно в одинаковой степени
|
| Рис. 6. Автокорреляционные функции для шума типа (1/f)g При g=1 недавнее и отдаленное прошлое почти в равной степени влияют на настоящее. |
коррелируют с событиями недавнего и очень отдаленного прошлого. Когда g близко либо к 0, либо к 2, события недавнего прошлого влияют на процесс гораздо сильнее, чем события отдаленного прошлого.
Поскольку функции автокорреляции свидетельствуют о том, что процесс типа 1/f сильно зависит от прошлого, особенно при g~1, можно задать вопрос, какое количество информации «помнит» процесс? Допустим, что процесс можно промоделировать с помощью линейной системы и что вся его прошлая история представлена текущими значениями переменных состояния системы. Сколько переменных состояния требуется для такой системы со спектром флюктуации типа 1/ f? Иначе говоря, сколько требуется чисел, чтобы суммировать влияние прошлого на настоящее? В случае белого шума количество таких чисел равно нулю. В случае броуновского движения оно равно единице (в одномерном случае) - требуется знать лишь начальное положение частицы. В случае шума типа 1/ f требуются сотни таких чисел - моделирующая процесс непрерывная RС-линия, которая в точности дает спектральную плотность мощности типа 1/ f, имеет бесконечное число переменных состояния. Это же справедливо для модели, представляющей собой сумму распределенных постоянных времени, которая была предложена Бернамоном [3] в 1937 г. для объяснения шума типа 1 /f в электровакуумных лампах. Однако если рассматривать линейную систему с сосредоточенными параметрами, которая дает лишь приближение к спектральной плотности мощности типа 1/ f, то требуются лишь сотни переменных состояния, причем с повышением нужной степени точности число переменных состояния возрастает медленно. Чтобы определить как верхний, так и нижний пределы для требуемого числа переменных состояния процесса типа 1/ f, рассмотрим линейную систему с сосредоточенными параметрами, отличную от RС-линии, введенной в разд. II. Эта модель будет использована также для иллюстрации сходства между процессами типа 1/ f, несколько отличающимися по параметру g.
|
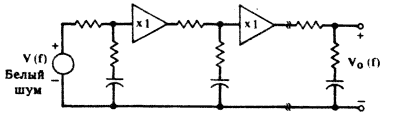
| Рис. 7. Еще одна линейная система, вырабатывающая шум, похожий на шум типа 1/f. Каждая секция имеет одну переменную состояния (напряжение на конденсаторе) и может «помнитьэ одно число. |
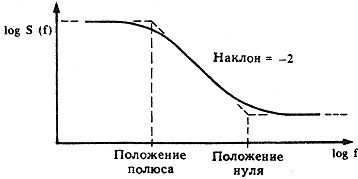
Можно выбрать простую линейную систему, спектральная плотность мощности которой будет отличаться от закона (1/ f)g на постоянную относительную величину, которая может быть сделана произвольно малой (рис. 7). Такая система имеет мало общего с предыдущей моделью, за исключением того, что она тоже представляет собой линейную систему, возбуждаемую источником белого шума, и что функция S(f) некоторой переменной V 0 (f) представляет собой зависимость вида 1/ f. Система состоит из резисторно-емкостных секций, разделенных и изолированных друг от друга буферными усилителями с единичным коэфффициентом усиления. Каждая секция вносит в суммарную частотную характеристику (отклик) системы один полюс и один нуль и имеет одну переменную состояния — напряжение на конденсаторе. Отклик одной секции приведен на рис. 8.
|
| Рис. 8. Частотная характеристика одной секции линейной системы, показанной на рис. 7. |
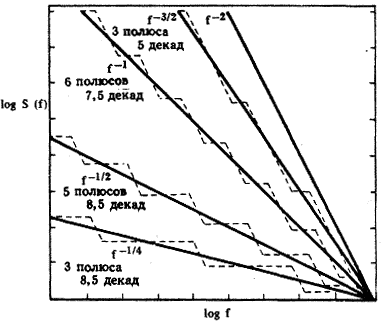
Требуемое число секций зависит, разумеется, от того, насколько точно должны совпадать приближенная и точная характеристики. Для точного совпадения потребовалось бы бесконечное число секций. Интересно, однако, определить, сколько секций требуется для аппроксимации с точностью ±5%, а затем на основе полученного значения обсудить вопрос о количестве переменных состояния и о количестве величин, необходимых для суммирования влияния прошлых событий на процесс типа 1/ f. Результаты такого расчета представлены на рис. 9 в двойном логарифмическом масштабе. Сплошные линии соответствуют спектральной плотности мощности для различных значений g. На каждую из этих линий наложена пунктирная линия, представляющая собой функцию S(f) аппроксимирующей линейной системы. Положения полюсов и нулей выбирались таким образом, чтобы максимальная ошибка лежала в пределах ±5%.
|
| Рис. 9. Аппроксимация спектральной плотности мощности типа 1/ f с различными значениями g с помощью линейных систем. Метки на осях абсцисс и ординат отстоят на 1 декаду. |
Результаты представляются несколько неожиданными. Для аппроксимации спектральной плотности мощности типа 1/ f требуется приблизительно одна секция (и также одна переменная состояния) на декаду изменения частоты. Несколько меньшее число секций нужно для аппроксимации зависимостей (1/ f)1/2 и (1/ f)3/2, а при приближении S(f) к белому шуму (g=0) или к броуновскому движению (g=2)требуемое число секций на декаду стремится к нулю. (Отметим, что для описания броуновского движения нужна всего одна переменная состояния.) Для аппроксимации спектральной плотности мощности 1/ f в полосе частот от 10-50 до 1050 Гц с погрешностью менее 5% требуется всего 100 секций. При погрешности 1% число секций должно быть, вероятно, менее 500. Это означает, что система будет иметь лишь несколько сотен переменных состояния и будет суммировать прошлые события с помощью лишь нескольких сот чисел. Даже если мы потребуем идеального совпадения, но будем наблюдать процесс в течение конечного интервала времени, число различимых переменных состояния, описывающих текущее поведение системы, не будет бесконечным - эффект конечного времени наблюдения (Tobs) состоит в сглаживании частотной характеристики за счет усреднения в полосе частот (f0), приблизительно обратной времени наблюдения
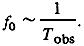
Самое большее, что нам потребуется — это полюс и нуль на каждое кратное f0. Таким образом, максимальное число различимых переменных состояния представляет собой отношение максимальной частоты измерения (f h) к величине, обратной времени наблюдения:
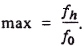
Чтобы сравнить этот результат с величиной, получающейся при 5%-ной точности аппроксимации, выберем низкочастотный предел измерения таким образом, чтобы он совпадал с наинизшей частотой, допускаемой временем наблюдения (влияние всех переменных состояния, постоянные времени которых намного превышают время наблюдения, может быть суммировано в одно текущее значение — кажущееся стационарное значение.) В результате получим пределы для числа переменных состояния (N):

Графики, приведенные на рис. 9, свидетельствуют о том, что шумы типа 1/ f с несколько различающимися значениями у имеют фундаментальное сходство между собой - у всех этих шумов равномерное распределение полюсов на декаду частоты, и в диапазоне значений 1/2<g<3/2 у них приблизительно одинаковое число полюсов на декаду. Главное различие систем с разными значениями g — это различие в относительном влиянии каждой из переменных состояния на текущее значение выхода системы.
В рамках настоящей статьи будем считать число переменных состояния, требуемых для аппроксимации с точностью 5%, минимальным числом, необходимым для описания данного процесса. Небольшое увеличение или уменьшение точности лишь незначительно повлияет на это число. Совместное рассмотрение выражения для минимального числа требуемых переменных состояния и выведенных ранее функций автокорреляции приводит к следующему описанию памяти шума типа 1/ f для значений g, очень близких к единице. Корреляция текущих событий с событиями, происшедшими время t назад, будет определяться напряжениями на всех конденсаторах, скорость разряда которых слишком мала, чтобы это напряжение могло существенно измениться за время t. В рассмотрение должны быть включены все конденсаторы, чьи полюсы находятся под напряжением достаточно низкой частоты, при условии, что эта частота всё же превышает наинизшую частоту f 0:
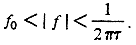
Поскольку каждый из конденсаторов равно влияет на текущее поведение системы, степень корреляции для случая g=1 пропорциональна суммарному числу таких конденсаторов:
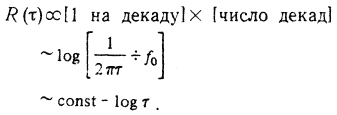
Как можно видеть, этот результат аналогичен полученному в разд. II.