Шум типа 1/f
Oб авторе
| 1/F NOISE Marvin S. Keshner Получена 7 апреля 1981 г., в исправленном виде —- 22 декабря 1981 г. Proceedings of the IEEE, 1982, vol. 70, № 3, p. 212—218. Manuscript received April 7. 1981; revised December 22, 1981. This work is based entirely on the Doctoral Dissertation of M. S. Keshner, supervised by W. M. Siebert and R. B. Adler and submitted (1979) to the Electrical Engineering and Computer Science Depsrtment of the Massachusetts Institute of Technology. | |
| The author is with Hewlett Packard Laboratories, Palo Alto, CA 94303. |
Шум типа 1 /f представляет собой нестационарный случайный процесс, который может служить моделью поведения эволюционирующих, или развивающихся, систем. В нем находит отражение сильное влияние прошлых событий на будущее и, следовательно, до некоторой степени предсказуемое поведение системы, а также влияние случайных событий. Выведены нестационарные автокорреляционные функции для шума типа 1/f, которые показывают, что текущее поведение системы в равной степени коррелирует с событиями недавнего и отдаленного прошлого. Показано, что минимальное количество памяти системы, вырабатывающей шум типа 1 /f, представляет собой одну переменную состояния на декаду изменения частоты. Прошлая история систем конденсируется в текущие величины переменных состояния, одна из которых представляет собой усреднение за одну (самую последнюю) единицу времени, другая — за 10 последних единиц времени, 100 единиц, 1000, 10 000 и т. д. Каждая такая переменная состояния равно влияет на поведение системы.
I. ВВЕДЕНИЕ
Шум типа 1/f представляет собой случайный процесс [1], который описывается кривой спектральной плотности мощности шума S(f). Мощность шума (или квадрат некой переменной, связанной со случайным процессом), измеренная в узкой полосе частот, приблизительно обратно пропорциональна частоте (рис. 1):
|
|
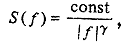
где 0<g<2 и g обычно близко к 1.
|
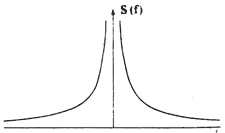
| Рис. 1. Спектральная плотность мощности шума типа 1/f. В отличие от белого шума, имеющего равномерную спектральную плотность на всех частотах, шум типа 1/f имеет повышенную плотность на низких частотах. |
Шум типа 1/ f впервые был обнаружен как избыточный низкочастотный шум в электровакуумных лампах, а затем, гораздо позже — в полупроводниках. Математические модели шума типа 1/ f, основанные на детальном рассмотрении физических процессов, были развиты Бернамоном [2] в 1937 г. для электровакуумных ламп и Макуортером [3] в 1955 г. для полупроводников. Начиная с середины 50-х годов, шум типа 1/ f наблюдался в виде флюктуации параметров различных систем. Многие из этих систем не имеют никакого отношения ни к электровакуумным лампам, ни к полупроводникам, и вырабатываемый ими шум типа 1 /f нельзя объяснить ни одной из упомянутых выше моделей. Так, например, шум типа 1 /f наблюдается в виде флюктуации [4, 5]
— напряжений и токов электровакуумных ламп, диодов, транзисторов;
— сопротивления угольных микрофонов, полупроводников, металлических тонких пленок, водных растворов ионов;
— частоты кварцевых генераторов;
— средних сезонных температур;
— годового количества осадков;
— интенсивности уличного движения;
— напряжения на нервных мембранах и синтетических мембранах;
— частоты приема инсулина диабетиками [61;
— экономических данных [7];
— громкости и высоты тона музыки [8].
Присутствие шума типа 1 /f в такой разнородной по составу группе систем (а также во многих других, не упомянутых здесь системах) заставило исследователей предположить, что существует некий фундаментальный закон природы, приложимый ко всем неравновесным системам и проявляющийся в шуме типа 1/ f. Были предложены многочисленные специфические модели, однако ни одна из них не может объяснить присутствие шума типа 1/ f хотя бы в большинстве из перечисленных систем. Возможно, единственным сходством между этими системами является их математческое описание, приводящее к зависимости типа 1/ f.
|
|
Тот факт, что шум типа 1/ f может быть применен к описанию флюктуации высоты тона и громкости многих видов музыки, дает серьезные основания предположить, что этот шум является менее случайным, чем другие виды шума, и что существует какое-то соотношение или корреляция между событиями, которые отсутствуют в других видах шума. Однако характер этого соотношения до настоящего времени оставался весьма туманным. Каковы временные шкалы, в пределах которых коррелируют события? Если прошлая история системы влияет на текущие события в ней, то в такой системе должен существовать какой-то механизм хранения информации, т. е. память. Какого рода память требуется для шума типа 1/ f? Какой объем информации и как долго «помнит» система? Эти вопросы рассматриваются в настоящей работе. Будет показано, что шум типа 1/ f пригоден для описания флюктуации в системах, развивающихся во времени.
В разд. II анализируется линейная система, вырабатывающая шум типа 1/ f, и выводится точная нестационарная функция автокорреляции. Если время, в течение которого наблюдается процесс, мало по сравнению с временем, прошедшим с начала процесса, то точную нестационарную функцию автокорреляции можно представить в приближенном виде. Полученная таким образом функция автокорреляции является почти стационарной, и с ее помощью можно описать память систем, вырабатывающих шум типа 1/ f.
|
|
В разд. III рассчитывается спектральная плотность мощности, соответствующая приближенной функции автокорреляции. Результаты расчета согласуются с экспериментальными данными, полученными при наблюдении шума типа 1/ f, в том отношении, что спектральная плотность мощности шума стационарна, за исключением того, что кажущееся стационарное значение логарифмически зависит от времени, прошедшего с момента начала процесса.
В разд. IV рассматривается другая линейная система и определяются пределы памяти системы. Хотя расчеты проводятся для физических систем, те же представления применимы к чисто информационным системам. Этот вопрос обсуждается в разд. V.
II. ШУМ ТИПА 1/f КАК НЕСТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
Интеграл спектральной плотности мощности для шума типа 1/ f при 1<g<2 (наиболее общий случай) равен бесконечности. Если бы шум типа 1/ f представлял собой стационарный случайный процесс, можно было бы заключить, что его дисперсия бесконечна и, следовательно, параметры процесса часто могут быть очень большими. Один из способов обойти эту трудность состоит в том, чтобы постулировать существование наинизшей частоты, ниже которой форма кривой спектральной плотности мощности изменяется таким образом, что интеграл становится сходящимся. Экспериментаторы, изучавшие шум типа 1/ f, усиленно пытались найти какие-либо признаки изменения формы кривой S(f) на очень низких частотах, однако самая низкая частота, на которой они могут точно измерить спектральную плотность мощности, ограничивается долговременной стабильностью их аппаратуры и тем временем, в течение которого они могут наблюдать случайный процесс. Несмотря на эти ограничения, одна группа экспериментаторов проводила измерения шума типа 1/ f в МОППТ на частотах вплоть до 10-6,3 Гц (период 3 недели) [91. Изменения формы спектральной кривой замечено не было. С помощью методики обработки результатов геологических исследований был проведен машинный расчет шума типа 1/f для погодных условий до частоты 10-10 Гц (период 300 лет) [10], и здесь тоже не наблюдалось никаких изменений формы спектральной кривой. Среди опубликованных результатов экспериментальных наблюдений можно найти только два случая, когда изменение было замечено: при наблюдении флюктуации сопротивления тонких пленок олова при температуре перехода в сверхпроводящее состояние [11] и при наблюдении флюктуации напряжения на нервных мембранах [12].
Другое решение проблемы бесконечной дисперсии было предложено Мандельбротом [13]. Он высказал предположение, что шум типа 1/ f при 1<g<2 следует рассматривать как нестационарный случайный процесс. В таком случае его дисперсия, а также его спектральная плотность мощности будут зависеть от времени. При наблюдении процесса в течение конечного промежутка времени всегда будет получаться конечная дисперсия. Но утверждать что-либо относительно текущего поведения исследуемой нестационарной системы можно, лишь зная ее точное состояние в некоторый предшествовавший момент времени (марковские процессы).
|
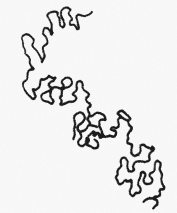
| Рис. 2. Путь частицы, находящейся в состоянии броуновского движения. |
Чтобы проиллюстрировать эту мысль, рассмотрим другой известный нестационарный случайный процесс - частицу, находящуюся в состоянии броуновского движения (рис. 2). Утверждать что-либо о текущем положении частицы можно лишь в том случае, если известно её положение в некоторый предшествовавший момент времени. Пусть, например, в момент t =0 частица находилась в центре поля наблюдения. В некоторый более поздний момент t =T она, по-видимому, должна находиться в пределах сферы радиуса R с центром вблизи ее начального положения. В еще более поздний момент радиус будет больше. При этом всегда среднее положение частицы является константой, равной ее начальной координате. Но дисперсия положения частицы, соответствующая квадрату радиуса сферы, в пределах которой частица, по всей вероятности, должна находиться, увеличивается линейно со временем. Если настаивать на том, чтобы описывать этот процесс как стационарный, и собирать данные во все моменты времени, то придётся заключить, что дисперсия является бесконечной, поскольку частица может с равной вероятностью находиться в любом месте. Но если описывать этот процесс как нестационарный и знать, где находилась частица в некоторый предшествовавший момент времени, то можно определить ее положение в некоторый последующий момент как случайную величину с конечной дисперсией.
В очевидном противоречии с предположением Мандельброта находится тот факт, что экспериментаторы обычно без особых трудностей измеряют спектральную плотность мощности шума типа 1/ f, не предполагая, что процесс является нестационарным, и ничего не зная о его начальном состоянии. Если бы процесс был нестационарным, то разве спектральная плотность мощности не должна была бы меняться в зависимости от времени и начальных условий? Экспериментаторы иногда обнаруживают изменения амплитуды спектральной плотности мощности при измерениях идентичных систем в различные моменты времени, но форма кривой и, в частности, величина показателя степени g остаются неизменными (см., например, данные, представленные Xуджем [14]).

|
| Рис. 3. Линия с сосредоточенными параметрами, являющаяся моделью непрерывной резистивно-емкостной линии передачи, которая возбуждается источником шумового тока с белым спектром. |
Мы начнем с детального рассмотрения простой системы, вырабатывающей шум типа 1/ f с g=1 и расчета ее нестационарной автокорреляционной функции. Эту процедуру можно обобщить на случай расчета нестационарной автокорреляционной функции любого шума типа 1/f с 0< g<2 [15]. Рассматриваемая ниже простая система представлена на рис. 3.
Система состоит из источника шумового тока величиной I с белым спектром, подключенного к входу одномерной непрерывной резистивно-емкостной линии передачи (RC- линии) бесконечной длины. Импеданс RС-линии бесконечной длины равен
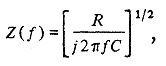
где R — погонное сопротивление линии, С — погонная емкость линии, j=Ö-1. Отсюда спектральная плотность мощности шума на входе линии равна
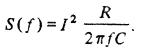
Отсюда видно, что если линия имеет бесконечную длину, то S(f) в точности пропорциональна 1/ f вплоть до нулевой частоты. Однако если линия конечна и на ее выходе включено сопротивление конечной величины, то будет существовать некоторая наинизшая частота, ниже которой спектр S(f) будет белым. Значение этой наинизшей частоты определяется длиной линии (l):
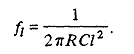
Чтобы получить выражение для нестационарной функции автокорреляции, будем считать линию бесконечной, а также что в момент времени t =0 напряжение на линии везде равно нулю. Выберем параметры источника белого шума таким образом, чтобы существенно облегчить вычисления - собственно говоря, это будет известный дробовой шум со средним значением, равным нулю. Рассмотрим процесс, вырабатывающий один раз в течение интервала времени Т единичный импульс тока, который с равной вероятностью может быть положительным или отрицательным и с равной вероятностью может возникнуть в любой момент внутри этого интервала:
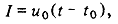
где u 0 (t — t 0) — импульс в момент времени t = t 0;
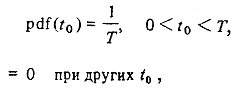
где pdf(t 0) — функция плотности вероятности от t 0. Суммирование большого числа (N) независимых идентичных процессов дает дробовой шум с белым спектром, определяемым выражением
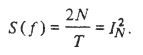
В нашем расчете увеличение интервала T будет сопровождаться соответствующим увеличением числа независимых процессов, так что величина S(f) будет оставаться постоянной. Это условие в точности эквивалентно условию постоянной скорости поступления для одиночного пуассоновского процесса.
При воздействии в момент t=t 0 импульса тока на RС-линию возникает отклик (по напряжению)
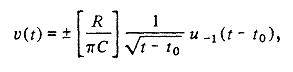
где

Функция автокорреляции для напряжения, возникающего при воздействии одиночного импульса
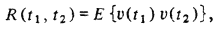
где E{ } — ожидаемое значение, равна:
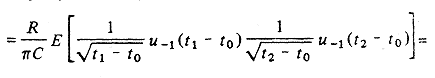

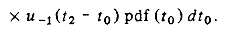
Учитывая, что оба члена отличны от нуля только при условии, что импульс возникает раньше, чем t 1 и t 2. и приняв t 2> t 1, получим

Для N идентичных и независимых процессов конечный результат будет представлять собой просто приведенное выше выражение, умноженное на N, т. е.
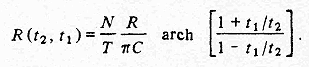
|
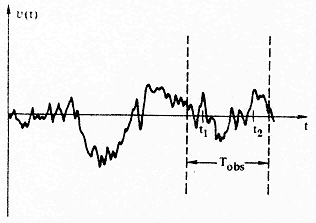
| рис. 4. Пример шума типа 1/f для случая, когда интервал времени наблюдения мал по сравнению с временем, прошедшим с момента начала процесса. |
Представим, что RС-линия существует очень давно, т. е. t 2 — большая величина, и что мы будем наблюдать процесс в течение сравнительно короткого времени T obs << t 2 Времена t 1 и t 2 будут находиться в пределах интервала наблюдения, но начальный момент t =0 не войдет в этот интервал. В результате отношение t 1 и t 2 будет почти равно единице (см. рис. 4). Тогда мы можем представить полученное ранее выражение в приближенном виде
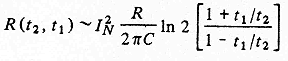
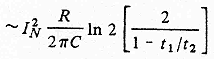
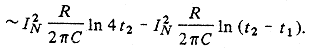
Эту процедуру легко обобщить на случай вывода функции автокорреляции для шума типа 1/ f, когда g не равно единице, а лежит в интервале 0<g<2. Подробное рассмотрение дано в работе [15], а здесь представлены лишь окончательные результаты. Для сравнения нестационарной и стационарной автокорреляционных функций величина (t 2— t 1) заменена на t.
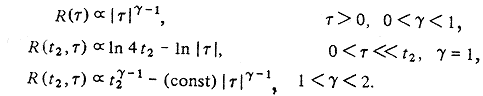
III. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ШУМА,
СООТВЕТСТВУЮЩАЯ ПРИБЛИЖЕННОЙ ФУНКЦИИ
АВТОКОРРЕЛЯЦИИ
Будем считать, что экспериментатор наблюдал систему в течение времени T оbs, гораздо меньшего, чем время, прошедшее с момента создания системы и начала процесса. Допустим также, что экспериментатор полагал, что он наблюдает стационарный случайный процесс, и рассчитал S(f), исходя из этого предположения. Каков был бы результат такого расчета?
В предыдущем разделе мы рассчитали нестационарные автокорреляционные функции для шума типа 1/ f. Затем эти функции были аппроксимированы для случая, когда время наблюдения (T obs) много меньше суммарного времени (t 2), прошедшего с момента начала процесса. Оказалось, что каждая приближенная автокорреляционная функция может быть записана в виде суммы двух членов — члена, зависящего только от t 2 и члена, зависящего только от t:
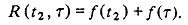
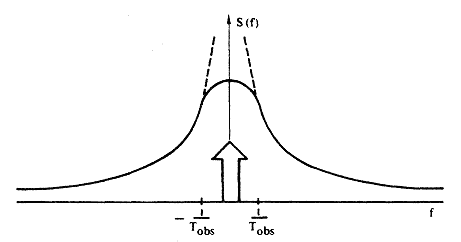
Фактически эти нестационарные автокорреляционные функции являются приближенно стационарными - нестационарное поведение полностью описывается дополнительным членом, зависящим только от t 2. Выполнив преобразование Фурье относительно переменной t, рассчитаем приближенно стационарную функцию S(f) и оценим влияние дополнительного члена. Поскольку нельзя наблюдать корреляцию в течение времени, превышающего суммарное время наблюдения Tobs, ограничим величину t пределами
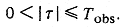
Разделив аргументы обоих членов в выражении для шума типа 1/ f при g =1 на T obs, получим
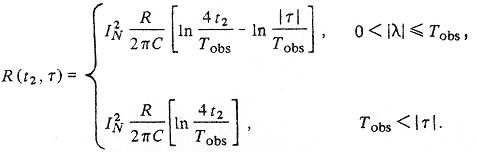
Используя сопряженное выражение для (1) из работы Эрдейи [16] и нормирующие свойства преобразований Фурье, получим для второго члена
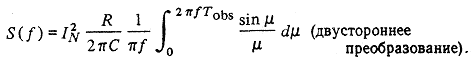
Результат преобразования первого члена относительно t представляет собой просто преобразование константы, которое дает импульс на нулевой частоте:

где u0 (f) — единичный импульс на f =0. Окончательный результат имеет вид
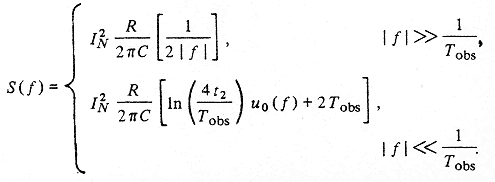
|
| Рис. 5. Спектральная плотность мощности, которая наблюдается при измерении шума на выходе моделирующей RC-линии. |
Эту спектральную плотность мощности иллюстрирует рис. 5. S(f) пропорциональна 1/ f вплоть до самой низкой частоты, ограничиваемой длительностью периода наблюдения. Как показатель степени, так и модуль S(f) на частотах, превышающих эту наинизшую частоту, не зависят ни от t 2, ни от T obs и, следовательно, стационарны. Кажущееся стационарное значение в интервале T obs будет представлять собой интеграл от S(f) для интервала
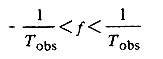
и будет равно
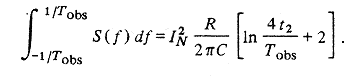
Нестационарная автокорреляционная функция, полученная в разд. II, соответствует спектральной плотности мощности, которая представляется стационарной. Измерения S(f), проведенные без знания начальных условий, будут непротиворечивыми в пределах диапазона частот, ограниченного временем проведения наблюдений. Дисперсия процесса возрастает со временем по логарифмическому закону, но проведение наблюдений в конечном интервале времени всегда дает конечную дисперсию.
В литературе принято нормировать функцию S(f) путем деления ее на квадрат стационарного значения параметра процесса. Когда независимый постоянный член не является преобладающим, величина S(f) будет логарифмически зависеть от t 2. Это может объяснить результаты некоторых экспериментальных наблюдений, когда показатель степени меняется незначительно, но сама величина функции меняется очень сильно.