| Число вкладов | До 3 | 3-5 | 5-7 | 7 и выше |
Определите с вероятностью 0,954 границы:
а) среднего вклада;
б) удельного веса вкладов до 5 тыс. руб.
Решение:
а) Сначала найдем средний вклад и выборочную дисперсию. Перейдем к дискретному ряду распределения.
Таблица 9
Расчетная таблица для вычисления среднего вклада
| Число вкладов | До 3 | 3-5 | 5-7 | 7 и выше | Суммы |

| |||||

| |||||

| |||||
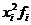
|
 тыс. руб. – средний размер вклада.
тыс. руб. – средний размер вклада.

Из условия задачи следует, что данная выборка является бесповторной, найдем среднюю ошибку выборки:

Найдем предельную ошибку выборки для данного уровня вероятности:
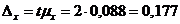 тыс. руб.
тыс. руб.
Таким образом, с вероятностью 0,954 границы среднего вклада (в тыс. руб.) являются следующими:


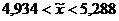
б) Найдем долю вкладов, каждый из которых по размеру не превосходит 5 тыс. руб.:
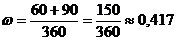
Найдем среднюю ошибку выборки при определении границ доли:

Предельная ошибка выборки для данного уровня вероятности:
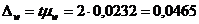
Таким образом, с вероятностью 0,954 границы доли вкладов, не превосходящих пяти тысяч рублей, являются следующими:



Или в абсолютном количестве вкладов:

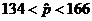
5) Имеются следующие данные по фабрике о производстве продукции за 1990-1995 гг. в сопоставимых ценах:
Таблица 10
Исходные данные пятой задачи
| Год | ||||||
| млрд. руб. | 67, 0 | 73,2 | 75,7 | 77,9 | 81,9 | 84,4 |
Для анализа ряда динамики определите:
а) средний уровень ряда динамики;
б) цепные и базисные темпы роста;
в) для каждого года абсолютное значение одного процента прироста, среднегодовой темп прироста.
Результаты расчетов изложите в табличной форме, сделайте выводы.
Решение:
а) Найдем средний уровень ряда динамики:
 млн. руб.
млн. руб.
б) – в) Для расчета показателей динамики используем следующие формулы:
Таблица 11
Используемые формулы
| Показатели | Базисные | Цепные |

| 
| 
|

| 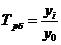
| 
|

| 
| 
|
Абсолютное содержание одного процента прироста: 
|
Вычисления сведем в таблицу:
Таблица 12
Показатели динамики
| Год | ||||||
| млрд. руб. | 67, 0 | 73,2 | 75,7 | 77,9 | 81,9 | 84,4 |
Абсолютный прирост базисный,  млрд. руб. млрд. руб.
| 6,2 | 8,7 | 10,9 | 14,9 | 17,4 | |
Темп роста базисный  , ед. , ед.
| 1,0925 | 1,1299 | 1,1627 | 1,2224 | 1,2597 | |
Темп прироста базисный  , ед. , ед.
| 0,0925 | 0,1299 | 0,1627 | 0,2224 | 0,2597 | |
Абсолютный прирост цепной,  млрд. руб. млрд. руб.
| 6,2 | 2,5 | 2,2 | 2,5 | ||
Темп роста цепной 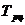 , ед. , ед.
| 1,0925 | 1,0342 | 1,0291 | 1,0513 | 1,0305 | |
Темп прироста цепной  , ед. , ед.
| 0,0925 | 0,0342 | 0,0291 | 0,0513 | 0,0305 | |
Абсолютное значение 1% цепного прироста  , млрд. руб. , млрд. руб.
| 0,67 | 0,732 | 0,757 | 0,779 | 0,819 |
Среднегодовой темп роста:
 ед.
ед.
Среднегодовой темп прироста:
 ед.
ед.
На протяжении 1990-1995 гг. наблюдается тенденция постоянного увеличения производства продукции на данной фабрике. При этом максимальный прирост наблюдался в 1991 году (+ 6,2 млрд. руб. или + 9,25%). Среднегодовой темп прироста составил +3,92%
6) По следующим данным постройте линейное уравнение регрессии, вычислите линейный коэффициент корреляции:
 ;
;  ;
;  ;
;  ;
;  ;
; 
Решение: Найдем средние квадратические отклонения величин  и
и  . Используем формулу для вычисления дисперсии:
. Используем формулу для вычисления дисперсии:


Вычислим коэффициент корреляции:

Вычислим коэффициент 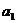 уравнения линейной регрессии:
уравнения линейной регрессии:
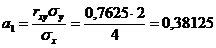
Таким образом, искомое уравнение регрессии:


7) Имеются данные о добыче угля и его себестоимости:
Таблица 13