Для решения задачи принятия решений в условиях неопределенности, когда из множества G допустимых решений Xi требуется выбрать оптимальное решение мы будем использовать несколько методов, таких как:
1. Критерий Лапласа
2. Минимаксный критерий
3. Критерий Сэвиджа
4. Критерий Гурвица



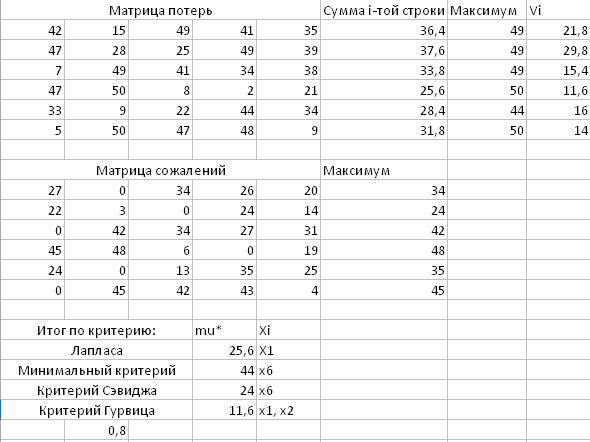
Тогда:
· По Лапласу лучшее решение - 4
· По Минимаксу лучшее решение - 5
· По Севиджу лучшее решение - 3
· По Гурвицу лучшее решение – 4
Окончательный ответ программы - 4 решение.
Матричные игры
Примем нашу матрицу потерь из (3.4) за платежную матрицу. Мы имеем двух игроков А и В. Нам необходимо определить для игрока А оптимальную смешанную стратегию в игре с платежной матрицей. Справедлива следующая основная теорема теории матричных игр с нулевой суммой.
Теорема. Каждая конечная игра с нулевой суммой имеет, по крайней мере, одно оптимальное решение среди смешанных стратегий.
Вектор P={p(i), I = 1:m} вероятностей, определяющий оптимальную сме-шанную стратегию игрока A в игре с платежной матрицей {М(i,j),i=1:m, j = 1:n} может быть найден из соотношения P={p(i), I = 1:m}’ = { Х(i), i = 1:m}’ / F, где F и X = { Х(i), I = 1:m} – решение следующей задачи ЛП.
F = sum(Х(i), i = 1:m) - > min
A’*X’ >= ones(m,1), X >= zeros(m,1).
Предполагается, что все элементы платежной матрицы положительны. В противном случае необходимо преобразовать платежную матрицу к виду, a(i,j)>0 путем добавления к её компонентам константы большей -min(a(i,j)).
Имеется нижеследующая платежная матрица:

Минимакс и максимин выделены особым цветом. Видно, что минимакс больше по значению, чем максимин, поэтому данная игра не имеет седловой точки и максиминно-минимаксные стратегии неоптимальны. Поэтому мы воспользуемся идеей смешанных стратегий, и попытаемся найти смешанные стратегии с заданными вероятностями для игрока А. Эти вероятности должны быть подобраны для максимизации наименьшего выигрыша по столбцам для игрока.
Поскольку все её элементы являются положительными, то применим теорию предыдущего пункта к задаче поиска оптимальной стратегии для игрока А. Будем искать решение следующей задачи: F = sum(X(i), i = 1:6) - > min при ограничениях:
42 * х1 + 47 * х2 + 7 * х3 + 47 * х4 + 33 * х5 + 5 * х6  1
1
15 * х1 + 28 * х2 + 49 * х3 + 50 * х4 + 9 * х5 + 50 * х6  1
1
49 * х1 + 25 * х2 + 41 * х3 + 8* х4 + 22 * х5 + 47 * х6  1
1
41 * х1 + 49 * х2 + 34 * х3 + 2 * х4 + 44 * х5 + 48 * х6  1
1
35 * х1 + 39 * х2 + 38 * х3 + 21 * х4 + 34 * х5 + 9* х6  1
1
х1, х2, х3, х4, х5, х6  0
0
Для решения данной ЗЛП воспользуемся пакетом LiPS, сформулировав задачу в табличной форме (рис. 21).

Рисунок 21. ЗЛП для нахождения смешанных стратегий игрока А.
Программа выдала нам следующий результат (рис. 22):
F = 0.029433; x5 = 0; x1 = 0,00903669; x2= 0,0066919; x3 = 0,0081452;
x4 = 0,00526493; x6 = 0,000294243
Тогда P = [0,00903669; 0,0066919; 0,0081452; 0,00526493; 0; 0,000294243]. Таким образом мы получили вероятности для максимизации наименьшего выигрыша по столбцам для игрока А.

Рисунок 22. Вероятности для смешанных стратегий игрока А.
Заключение
В результате выполнения курсовой работы был освоен инструментальная экспертная система программного комплекса MALT - системы поддержки принятия решений в условиях определенности по количественным и качественным критериям.
Изучена теория благосостояния: эгалитаризм и утилитаризм.
Реализован метод размещение объекта коллективного пользования на
кольцевой дороге.
Создано программное средство на основе имеющейся теоретической
базе по совместному финансированию объекта и дележу продуктов.
Были освоены методы и алгоритмы решения задач принятия решений
в условиях неопределенности, приобретены навыки и умения разработки
математического обеспечения поддержки принятия решений на основе
реализации стандартных и модифицированных алгоритмов теории
исследования операций.
Список использованной литературы
1. Мулен Э. Кооперативное принятие решений: аксиомы и модели: М.:
Мир, 1991. – 464 с.
2. Ларичев О. И. Теория и методы принятия решений, а также Хроника
событий в Волшебных Странах: Учебник. - М.: Логос, 2009. -296 с.
3. Нейман Дж. фон, Моргенштерн О. М. Теория игр и экономическое
поведение..: Наука, 1970.
4. Канторович Л. В., Горстко А. Б. Оптимальные решения в экономике.
М.: Наука, 1972.
5. П. Конюховский. Математические методы исследования операций в
экономике. С.-Пб.: Питер, 2000.
6. Косоруков О. А., Мищенко А. В. Исследование операций. Учебник для
вузов. М.: Экзамен, 2003.
7. Костюкова О. И. Исследование операций. Минск: БГУИР, 2003.
8. Кофман А., Анри-Лабордер А. Методы и модели исследования
операций. М.: Мир, 1977.
9. Крушевский А. В. Теория игр. Киев: «Вища школа», 1977.
10.Дж. Моулдер, С. Элмаграби. Исследование операций. В 2 томах. М.:
Мир, 1981.