ЗАДАНИЕ
на курсовую работу по дисциплине
«Теория принятия решений»
Тема: «Нахождение оптимальных решений некоторых задач организации бизнеса по продаже планшетных ПК»
Исходные данные: необходимо решить четыре задачи организации бизнеса.
Первая задача: выбор по определённым критериям, с точки зрения
«покупатель», системный блок из ряда вариантов.
Вторая задача: размещение объекта коллективного пользования на кольцевой
дороге в случае двух пользователей при наличии препятствия на дороге.
Третья задача: нахождение оптимального распределения затрат на
общественный проект.
Четвертая задача: принятие решений в условиях неопределенности, когда из
множества G допустимых решений Xi требуется выбрать
оптимальное решение.
Руководитель работы: _____________________ _____ Коледов Л.В.. __
(подпись) (Ф.И.О преподавателя) (Ф.И.О).
Задание принято к выполнению:
«___»_________2012г. _____________________ Иманов Т.С
(дата) (подпись) (Ф.И.О. студента)
Ростов-на-Дону
Оглавление
Введение……………………………………………………………………………4
1. Анализ проблемы …………………………………………….…………………5
2. Постановка задачи…………………………………………….………………...6
3. Ход выполнения работы...…………………………………................................8
3.1. Выбор планшетного ПК при помощи инструмента MALТ………………...8
3.2. Размещение объекта коллективного пользования...……………………….11
3.3.1. Распределение затрат на общественный проект........................................15
3.3.2. Дележ продуктов……………………….........…………..............................16
3.4. Принятие решений в условиях неопределенности………………………...23
3.5. Матричные игры……………………………………………………………..25
Заключение………………………………………………………...……………...27
Список использованной литературы……………………………....…………….28
Введение
Вероятно, многие начинающие бизнесмены задаются вопросом, с
чего начать строить свое дело или бизнес. В какие инструменты экономики
вложить свои финансы. К одним из таких инструментов, среди многих,
можно отнести ведение бизнеса.
Итак, как организовать свой бизнес и удачно вложить свой капитал.
Наверно многие начинающие путь в тернии Бизнеса, ищут вопрос с чего
начать? Я отвечу на этот вопрос просто. Любой бизнес начинается с удачно
составленного бизнес - плана, в котором просчитаны все аспекты будущего
предприятия.
Проще и удобнее сразу строить бизнес как систему. Несложно заложить фундамент системы бизнеса в самом начале, когда бизнес еще маленький. Чтобы серьезно переделывать бизнес, который уже разросся, потребуется на порядок больше сил и средств.
И поэтому в самом начале (при построении бизнес - плана) необходимо оптимально решить множество разнообразных задач, которые можно классифицировать и решить оптимальным способом для получения максимального результата полезности.
Анализ проблемы
Задача курсовой работы заключается в написании четырех задач
организации бизнеса:
1. выбор по определённым критериям, с точки зрения покупателя,
планшетного ПК из ассортимента магазина;
2. размещение объекта коллективного пользования на кольцевой дороге в случае двух пользователей при наличии препятствия на дороге;
3. нахождение оптимального распределения затрат на общественный
проект;
4. принятие решений в условиях неопределенности, когда из множества G допустимых решений Xi требуется выбрать оптимальное решение.
Для решения поставленной задачи будет использоваться инструментальная экспертная система программного комплекса MALT - система поддержки принятия решений в условиях определенности по количественным и качественным критериям.
Так же для решения задач в случае неопределенности, основным пакетом будет является MATLAB. Это набор прикладных программ для решения задач технических вычислений и одноимённый язык программирования, используемый в этом пакете. Данный продукт позволяет решать задачи линейного программирования, к которым сводятся задачи с неопределенностью.
Постановка задачи
Задача 1. По определённым критериям необходимо выбрать, с точки
зрения покупателя, планшетный ПК из ассортимента магазина.
Задача 2.1. Требуется найти оптимальное положение объекта коллективного пользования, которым будут пользоваться жители городов A и B. Маршрут, по которому можно достичь объекта, составляет кольцо, на котором имеется участок, где объект невозможно разместить по техническим причинам. Для удобства описания, на кольце введем периодическую систему координат, такую, что город A имеет координату '0', город B имеет координату 'B', объект Z имеет координату 'n', полная протяженность (период) равен N, координаты границ запрещенных участков дороги обозначены через B, g2.
Задача 2.2. Требуется найти оптимальное положение объекта коллективного пользования, которым будут пользоваться жители городов A и Bi. Маршрут, по которому можно достичь объекта, составляет кольцо. Для удобства описания, на кольце введем периодическую систему координат, такую, что город A(1) имеет координату '0', город A(i) имеет координату ' A(i)', объект Z задается координатой 'n', полная протяженность (период) равен N.
Задача 3.1. Нижеследующую задачу можно рассматривать как приложение лексиминного порядка. Требуется найти оптимальное распределение затрат (х1,..., хn) между n агентами, намеревающимися финансировать проект, стоимость реализации которого составляет c, а потребления результата реализации агентами составят величины (b1,..., bn).
Задача 3.2. Два агента получили в качестве общего подарка ‘lb’ фунтов печенья и ‘lw’ литров вина и должны поделить этот подарок между собой. Предпочтения обоих агентов являются линейными (кривые безразличия суть параллельные прямые линии). Но предельные коэффициенты замещения различаются: агент 1 один фунт печенья ценит как ‘uc1’, один литр вина как ‘uw1’, а агент 2 – соответственно как ‘uc2’ и ‘uw2’.
Задача 4. Рассмотрим задачу принятия решений в условиях неопределенности, когда из множества G допустимых решений Xi требуется выбрать оптимальное решение X G, где i i n G X 1.. { }. Пусть S j - одно из возможных состояний изучаемой системы из множества S всех возможных ее состояний S S j j m 1.. { }. Тогда каждому S j S соответствует свой результат ij (Xi, S j); (j 1.. m), определяющий выигрыш (потери) при принятии данного решения Xi и реализации данного состояния S j. Такие ij образуют матрицуисходных данных для принятия решения ν (G, S) { ij }, i 1.. n, j 1.. m (1). Если ij определяют выигрыш (доход) или потери (затраты), то и ν (G, S) называется матрицей выигрышей или потерь, соответственно.
Ход выполнения работы
3.1. Выбор планшетного ПК при помощи инструмента MALT.
В качестве критериев выбраны:
· Цена;
· Камера;
· Емкость аккумулятора;
· Объем памяти;
· Диагональ экрана;
Все критерии, кроме «камера» являются количественными. Критерии изображены на рисунке 1:

Рисунок 1. Таблица критериев.
В качестве альтернатив был выбран ассортимент знаменитого магазина под названием «MediaMarkt».(рисунок 2.):
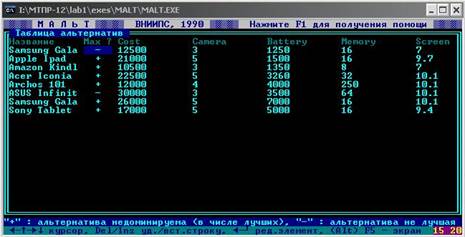
Рисунок 2. Таблица альтернатив.
Количество недоминируемых альтернатив по Парето 6 из 8 альтернатив

Рисунок 3 Сравнения альтернатив по Парето
В результате были выбраны следующие предпочтения с точки зрения покупателя(рисунок 3):

Рисунок 4 Список предпочтений.
После занесения предпочтений, количество недоминируемых альтернатив равно 5.
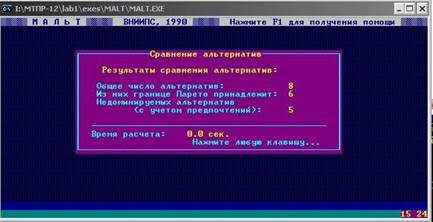
Рисунок 5 Сравнения с учетом предпочтений.
Размещение объекта коллективного пользования
Координата А = 0; B = 237.0934; g2 = 295.0934; N = 340;
| A | B | g2 | N |
| 237.0934 | 295.0934 |
Для начала надо построить графики полезностей для городов. Характеристикой полезности для каждого города является расстояние искомого объекта n до каждого города A и B. Для показательности и построения полезностей отдельно построим зависимости расстояния от нужного объекта до определенного населенного пункта А или B в зависимости от размещения объекта n в определенной координате. Графики расположены на рисунках 6 и 7.

Рисунок 6. График полезности для города А.

Рисунок 7. График полезности для города В.
Далее руководствуясь эгалитарным принципом, строим зависимость выражающее максимально возможное расстояние до какого-либо города от выбранной координаты (рис 8.)

Рисунок 8. Максимальное расстояние до одного из городов.
Из графика (рис. 8) видно, что эгалитарное решение находится в точке 110. Исходя из заданных условий, мы можем сделать вывод, что при размещении объекта n в заданную точку в этой координате мы не заходим на недопустимую зону. Это можно увидеть при построении множества допустимых полезностей для городов А и B, где полезность – отрицательная величина от расстояния каждого города (рис. 10). Полезность для города А и В примерно составляет -110 единиц.

Рисунок 9. Полезности для городов А и В.
2. Координаты A(i) города соответственно равны 4 14 24 26 46.
| A(2) | A(3) | A(4) | A(5) | A(6) |

Рисунок 10. Графики всех функций расстояния.
Для графического решения задачи размещения объекта по эгалитарному признаку необходимо построить график максимумов расстояний для каждого из городов (рис. 11). А для решения по утилитарному признаку нужно смотреть по построению графика суммы расстояний от каждого города в соответствующей координате (рис. 12).

Рисунок 11 Максимумы расстояния для всех городов

Рисунок 12 Сумма расстояний до каждого города.
Для нахождения решения максимальной полезности необходимо найти минимальное расстояние. Соответственно, что по утилитарному, что по эгалитарному критерию размещение объекта в координате 13 дает нам наибольшую полезность.