Теорема
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство (см. Рис. 1)
Чтобы доказать эту теорему, ее нужно свести к предыдущей, которую мы знаем. Мы знаем, как находить площадь треугольника.
Разобьем трапецию на два треугольника,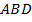 
и 
, и 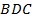используем свойство площади любого многоугольника.
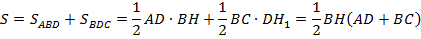
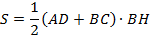
ч. т. д.
Задача 1
По рисунку 2, где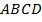 
– трапеция, найдите ее площадь.
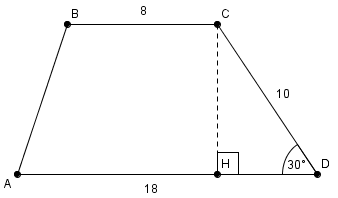
Рис. 2. Иллюстрация к задаче 1
Решение
Нам известно основание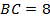 
, 
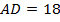, боковая сторона 
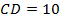и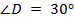 
. Надо найти площадь трапеции. Нам не хватает высоты, значит задача сводится к нахождению высоты. Для ее нахождения нам нужно выбрать удобную точку, из которой мы и проведем высоту. Такой точкой является точка 
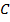. Проведем перпендикуляр 
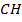на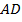 
и рассмотрим треугольник 
.
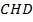Этот треугольник прямоугольный, с углом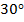 
. Мы знаем свойство такого треугольника: катет, лежащий против угла в тридцать градусов, равен половине гипотенузы.
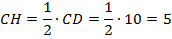
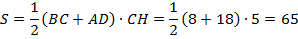
Ответ: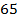 
.
Задача 2
Найти площадь прямоугольной трапеции, у которой две меньшие стороны равны по 6 см, а больший угол равен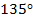 
(см. Рис. 3).
Решение
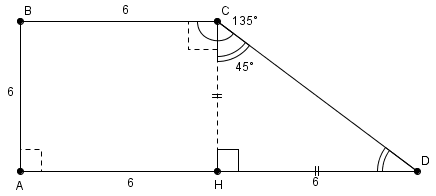
Рис. 3. Иллюстрация к задаче 2
Для нахождения площади нам нужна высота. Из точки 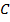опустим перпендикуляр 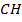, и получим высоту.
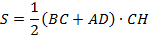
Перпендикуляр 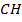делит угол 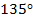на угол 
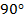и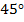 
. А раз этот угол 45 градусов, значит, угол 
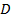тоже 45 градусов. Треугольник 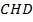– прямоугольный, а четырехугольник 
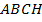– квадрат, потому что противоположные стороны параллельны, а смежные стороны равны между собой и хотя бы один из углов равен 90 градусов.
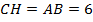
Теперь найдем 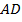, этот отрезок состоит из отрезка 
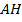, который равен 6, и из отрезка 
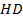, который также равен 6, потому что треугольник 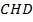– равнобедренный (углы при основании равны) и 
.
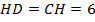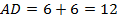
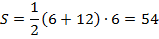
Ответ: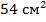 
.
|
|
Задача 3
В трапеции 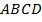c основаниям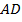и и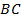 
проведены диагонали, они пересекаются в точке 
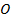. Доказать, что треугольник 
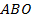равновелик треугольнику 
(см. Рис. 4).
Решение
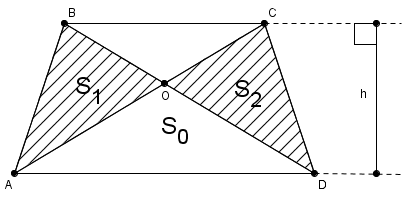
Рис. 4. Иллюстрация к задаче 3
Диагонали трапеции рассекают ее на четыре треугольника. Два треугольника примыкают к боковым сторонам. Нужно доказать, что в любой трапеции такие треугольники равновелики.
Рассмотрим треугольник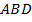и и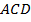 
. Они равновелики, т. е. имеют одинаковые площади.
1) 
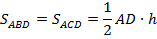(так как у них одно основание и высота)
2) 
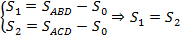
ч. т. д.
Задача 4
Найти площадь равнобедренной трапеции, у которой меньшее основание 18 см, высота 9 см, меньший угол 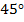(см. Рис. 5).
Дано: 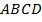– трапеция (
)
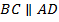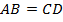
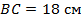
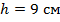
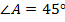
Найти: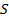 
Решение
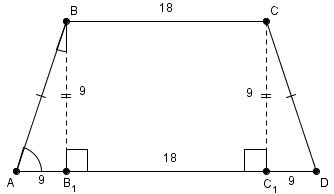
Рис. 5. Иллюстрация к задаче 4
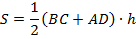
Задача сводится к нахождению большего основания .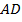
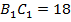– потому что 
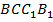прямоугольник (стороны 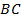и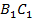 
– параллельны, две другие стороны тоже параллельны как перпендикуляры к параллельным прямым)
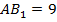, потому что треугольник 
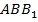– прямоугольный и равнобедренный, так как два его угла равны 45 градусов, значит, 
.
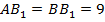Аналогично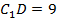 
.
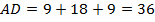
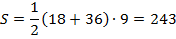
Ответ: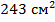 
.
Задача 5
Найти площадь равнобедренной трапеции, у которой высота равняется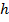 
, а диагонали взаимоперпендикулярны (см. Рис. 6).
Дано: ;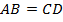 
;
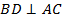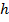– высота.
Найти: .
Решение
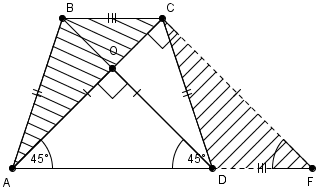
Рис. 6. Иллюстрация к задаче 5
Важную роль здесь играют диагонали.
Проведем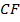 
параллельно 
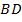. Получим треугольник 
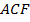и параллелограмм 
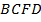(противоположные стороны 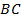и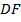 
параллельны по условию, 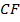параллельно 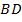по построению).
Диагонали трапеции перпендикулярны и равны между собой и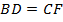 
, а значит, треугольник 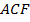– равнобедренный и прямоугольный.
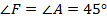
Далее докажем, что площади треугольников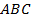 
и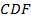 
равны.
|
|
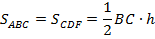, так как 
.
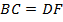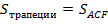(мы отняли площадь одного треугольника 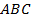и добавили площадь треугольника ).
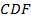Треугольник 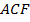, во-первых, равнобедренный, во-вторых, у него известна высота, опущенная из вершины 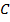, значит, его площадь можно найти (см. Рис. 7).
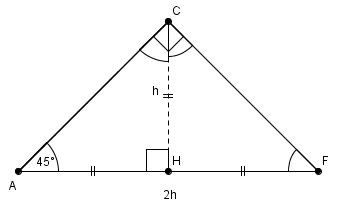
Рис. 7. Треугольник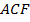
Высота треугольника 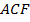является и биссектрисой, и медианой, значит, отрезок 
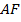– гипотенуза, равняется 
.
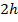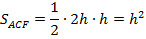
Ответ: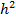 
.
Задача 6
Дана трапеция с основаниями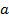 
, 
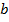и высотой 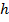. Проведена средняя линия 
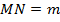. Доказать, что площадь трапеции равна средней линии 
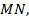умноженной на высоту (см. Рис. 8).
Дано: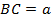 
; 
;
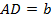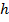– высота;
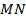– средняя линия.
Доказать: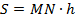 
.
Доказательство
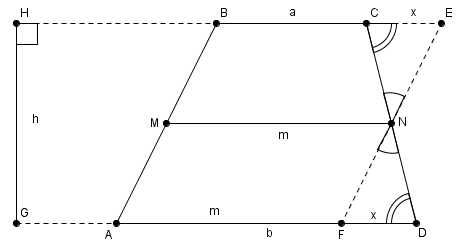
Рис. 8. Иллюстрация к задаче 6
Через точку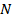 
проведем прямую 
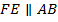, получим точки 
, 
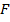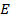, треугольники 
(
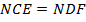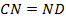по условию, прилегающие углы равны, 
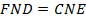как вертикальные, углы 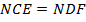как накрест лежащие при пересечении параллельных прямых 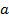и 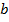секущей 
).
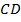Из равенства треугольников вытекает, что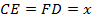 
.
Теперь у нас есть два параллелограмма,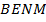 
и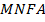 
. Эти четырехугольники – параллелограммы по определению, потому что противоположные стороны параллельны.
Если среднюю линию мы обозначили как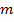 
, то 
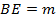и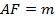 
.
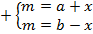
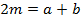
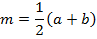
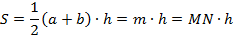
ч. т. д.
Заключение
На этом уроке мы доказали формулу для нахождения площади трапеции. Площадь равна полусумме оснований, умноженных на высоту. Закрепили эту формулу решением задач.
Домашнее задание: выполнить тестовое задание: 4 задачи с вариантами ответов (присылаете только номер вопроса-цифра ответа), а задачу №5 необходимо решить и прислать решение. Удачи!
Проверочный тест по теме
"Площадь трапеции" (8 класс)
I вариант:
1. Найдите площадь трапеции АВСД, если ее основания равны 5см и 9см, а высота 6см.
|
|
Варианты ответов:
1) 21
2) 54
3) 42
4) 84
Ответ: ___
2. В равнобедренной трапеции угол при основании равен 45, а основания равны 6см и 10см. Найдите площадь трапеции.
Варианты ответов:
1) 16
2) 32
3) 24
4) 8
Ответ: ___
3. В прямоугольной трапеции основания равны 5см и 9см, меньшая боковая сторона равна 4см. Найдите площадь трапеции.
Варианты ответов:
1) 36
2) 56
3) 28
4) 14
Ответ: ___
4. Диагонали трапеции взаимно перпендикулярны и равны 12см и 18см. Найдите площадь трапеции.
Варианты ответов:
1) 108
2) 216
3) 162
4) 54
Ответ: ___
5. Основания и высота трапеции относятся как 5:6:4. Найдите меньшее основание трапеции, если площадь трапеции равна 88см2.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________