Формально-кинетические закономерности восстановления оксидов металлов газами

Количественный анализ кинетических закономерностей топохимических реакций, том числе реакций, очень сложен. Однако, рассмотрев несколько идеализированных случаев восстановления, можно выяснить влияние ряда факторов на кинетику рассматриваемого процесса.

Упражнение 1. На основе общих положений химической кинетики обратимых адсорбционно-химических реакций получить кинетическое уравнение для описания скорости процесса восстановления в кинетическом режиме.

Решение. Если процесс не лимитируется сложной в кинетическом описании кристаллохимической стадией зарождения новой фазы, то обратимую реакцию восстановления можно представить схемой

Скорость ее равна: , (1)

где и – константы скорости прямой и обратной реакций.

Так как общее давление газа ,

то

При равновесии или

где – равновесное давление восстановителя.

Обозначив

имеем (2)

Полученное уравнение показывает, что скорость процесса определяется величиной реакционной поверхностью, температурой и давлением газа на реакционной поверхности.

Если диффузия газа к поверхности реакционной не затруднена (кинетический режим), то ,

где – парциальное давление газа-восстановителя в объеме реактора,

и уравнение (2) принимает вид:

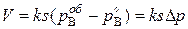(2а)

Следует отметить, что при более строгом выводе данного уравнения с учетом адсорбционно-десорбционных явлений, получаются более сложные зависимости.

Упражнение 2. Исходя из допущения о сферической форме частиц оксида металла, получить кинетическое уравнение зависимости степени восстановления оксида от времени для процесса, протекающего в кинетическом режиме.

Решение. Если исходный оксид состоит из частиц сферической формы с начальным радиусом r_o и имеет массу m_o, то к моменту времени t произойдет изменение массы и радиуса , где m и r – масса материала и радиус частиц к моменту времени t. Тогда степень восстановления α исходного оксида . Для каждой из частиц , где – плотность вещества.

Подставляя массы в выражение для , получаем и . (3)

Скорость процесса V, выраженная через изменение количества (моль) исходного вещества в единицу времени

, (4)

где M – молярная масса вещества.

Сравнивая полученное выражение с уравнением (2а) для скорости процесса в кинетическом режиме и учитывая в последнем , получим

и . (5)

При постоянных значениях температуры (k), давления, а значит, и , а также молярного объема скорость уменьшения размера непрореагировавшей части исходного оксида постоянна, то есть . После интегрирования этого уравнения от 0 до t и от r_o до r получаем или .

Записав отношение размера непрореагировавшей части исходного оксида к начальному размеру через степень восстановления приходим к уравнению

. (6)

Это уравнение, приведенное к форме

, (6а)

известно как закономерность модели сжимающегося объема или как уравнение Мак-Кевана. Оно предполагает быстрое образование границы раздела фаз с последующим линейным во времени продвижением реакционной зоны в объем сферического зерна.

Для полного завершении восстановления () требуется время

. (7)

Оно, как видно, уменьшается с уменьшением размера частиц материала, с ростом температуры, что соответствует увеличению константы скорости, с увеличением фактического парциального давления газа-восстановителя в объеме реактора, что соответствует увеличению .

Дополнение.

Упражнение 2а. Исходя из допущения о кубической форме частиц оксида металла, получить кинетическое уравнение зависимости степени восстановления оксида от времени для процесса, протекающего в кинетическом режиме.

Решение. Если исходный оксид состоит из частиц кубической формы с начальным размером ребра куба r_o и имеет массу m_o, то к моменту времени t произойдет изменение массы и размера , где m и r – масса материала и размер частиц к моменту времени t. Для каждой из частиц , где – плотность вещества. Подставляя массы в выражение для степени восстановления исходного оксида

получаем и . (3а)

Скорость процесса V, выраженная через изменение количества (моль) исходного вещества в единицу времени

, (4а)

где M – молярная масса вещества.

Сравнивая полученное выражение с уравнением (2а) для скорости процесса в кинетическом режиме и учитывая в последнем поверхность куба , получим

и . (5а)

Интегрируем (5а) и получаем:

или .

Так как , то и получаемуравнение Мак-Кеванав форме

, (6а’)

где .

 

Упражнение 3. На основе общих положений диффузионной кинетики получить кинетическое уравнение для описания скорости процесса газового восстановления оксида металла в диффузионном режиме. Исходя из допущения о сферической форме частиц соединения, получить кинетическое уравнение зависимости степени превращения от времени для процесса, протекающего в диффузионном режиме.

Решение. Если в процессе восстановления продукт оказывается малопористым, плотным, то имеются значительные диффузионные торможения, и процесс может осуществляться в диффузионном режиме. Адсорбционно – кристаллохимические реакции идут быстро, и поэтому в порах на границе раздела фаз устанавливается давление, близкое к равновесному 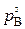, и соответствующая ему концентрация газа .

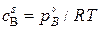На наружной поверхности частично прореагировавшего зерна устанавливается концентрация , соответствующая давлению в объеме газа при отсутствии внешнедиффузионных торможений.

Скорость диффузии газа через слой оксида в соответствии с законом Фика

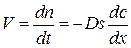. (8)

Для процесса со сферической формой частиц , (9)

где – радиус сферы в слое оксида, изменяющийся от r_o до r за время t.

При решении этого уравнения возможны несколько различных допущений.

В первом приближении для квазистационарного процесса градиент концентрации может быть заменен отношением приращений .

Тогда . (10)

Введя в данное выражение скорость из выражения

, (4)

получим (11)

Разделим переменные и проинтегрируем

.

Тогда , (12)

то есть толщина слоя изменяется во времени по параболическому закону . Введя с помощью уравнения (3), приходим к уравнению

, (13)

которое известно как уравнение Яндера. Оно является приближенным для частиц сферической формы, так как связь толщины слоя с радиусом непрореагировавшей части частицы малого размера оказывается более сложной.

 

Более строгий учет сферической симметрии может быть выполнен следующим образом.

Уравнение (9) запишем в виде .

Интегрируя в приближении независимости скорости диффузионного потока от x ,

получаем или . (14)

Сопоставление уравнений (14) и

, (4)

дает выражение для линейной скорости перемещения реакционной зоны

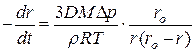, (15)

из которого видна более сложная, чем из (10) зависимость линейной скорости от размера r непрореагировавшей части оксида. На начальном этапе, когда

сферическая симметрия частиц не проявляется, то есть линейная скорость, как и в предыдущем случае, обратно пропорциональна толщине оксидного слоя (). Затем при с дальнейшим утолщением слоя продукта диссоциации (с уменьшением r) линейная скорость возрастает.

Интегрирование уравнения (14) и введение степени превращения 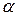через отношение 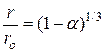(3) приводит к кинетическому уравнению

. (16)

Это уравнение, приведенное к форме

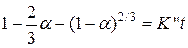, (16а)

известно как уравнение Кранка, Гистлинга и Браунштейна.

Это уравнение более точное по сравнению с уравнением Яндера, так как было учтено изменение объема сферы по ходу реакции.

Из уравнения (16) время полного завершения восстановления оксида ()

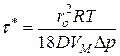. (17)

Сравнение с уравнением (7) для времени завершения процесса в кинетическом режиме приводит качественно к тем же выводам.

Однако для процесса в диффузионном режиме следует отметить более сильное влияние размера зерен оксида и менее сильное влияние температуры, так как к сильному уменьшению за счет экспоненциального роста с ростом температуры добавляется некоторое увеличение с ростом величины T, находящейся в числителе уравнения (17).

Пример 10. В таблице представлены экспериментальные данные по кинетике восстановления оксида никеля водородом (α – степень восстановления):

Время t, час
α,%	1200°С		0,055	0,12	0,236	0,306	0,437
1300°С		0,11	0,25	0,447	0,632	0,764
1400°С		0,27	0,414	0,765	0,989

Представить данные графически. Проверить применимость к описанию кинетики данного процесса простых формально-кинетических уравнений связи степени превращения со временем. Сделать вывод о режиме протекания процесса. Вычислить энергию активации процесса.

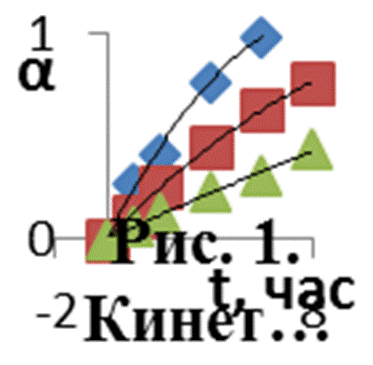Решение. Представим данные опыта графически (рис.1).

Видно, что в условиях опытов временная зависимость давления продукта имеет монотонный характер, и автокаталитический период отсутствует.

Проверим применимость для описания кинетики процесса уравнения Мак-Кевана

, которое можно представить уравнением ,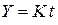

где

Результаты вычисления функции Y даны в таблице.

 

t, час
Y	1200°С		0,019	0,042	0,086	0,115	0,174
1300°С		0,038	0,091	0,179	0,283	0,382
1400°С		0,100	0,163	0,383	0,778

На рис 2 представлены значения функции Y в зависимости от времени при температурах опытов. Линии проведены с помощью одной из расчетно-графических программ ЭВМ, показаны уравнения линий и коэффициенты корреляции переменных.

Видно, что требуемая уравнением Мак-Кевана линейность функции 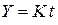выполняется достаточно удовлетворительно. Можно заключить, что процесс протекает в кинетическом режиме.

 

Проверим применимость для описания кинетики процесса уравнения Яндера

, которое можно представить уравнением ,

где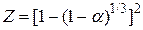

Результаты вычисления функции даны в таблице.

t, час
Z	1200°С		0,0003	0,0017	0,0074	0,0131	0,0304
1300°С		0,0015	0,0084	0,0321	0,0803	0,1459
1400°С		0,0099	0,0266	0,1466	0,6047

На рис 3 представлены значения функции Z в зависимости от времени при температурах опытов. Видно, что требуемая уравнением Яндера линейность функции не выполняется.

Можно без проверки полагать, что и уравнение Кранка, Гистлинга и Браунштейна

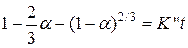, которое как и уравнение Яндера описывает кинетику процесса в диффузионном режиме, также будет не применимым для представленных опытов.

Степень восстановления характеризует скорость процесса. Поэтому уравнение Аррениуса 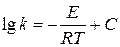можно записать в виде ,

где E – кажущаяся энергия активации, а в константу входит коэффициент пропорциональности между константой скорости и степенью восстановления .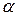

Для вычисления энергии активации представим уравнение Аррениуса графически в координатах . Вычисленные значения этих величин при заданной продолжительности восстановления представлены в таблице и графически (рис. 4)

 

T,°С	T, K	1/T
		0,000679	-1,260	-0,921	-0,627	-0,514	-0,360
		0,000636	-0,959	-0,602	-0,350	-0,199	-0,117
		0,000598	-0,569	-0,383	-0,116	-0,005

Найденные обобщенные константы скорости процесса восстановления, входящие в уравнения Мак-Кевана при температурах опытов, представим в таблице:

 

T, K	K	1/T	lg K
	0,020	0,000679	-1,6990
	0,047	0,000636	-1,3279
	0,116	0,000598	-0,9355

 

На основании данных таблицы построим график в координатах , который соответствует уравнению Аррениуса 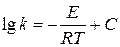. Здесь E – кажущаяся энергия активации гетерогенного процесса.

На графике приведено уравнение прямой линии и коэффициент корреляции переменных.

Вычисленное из углового коэффициента прямой кажущаяся энергия активации составляет . Такое значение энергии активации характерно для гетерогенных процессов, протекающих в кинетическом режиме.

 

 

Линии проведены с помощью расчетно-графической программы ЭВМ, показаны уравнения линий и коэффициенты корреляции переменных.

Характерна практически проявляющаяся параллельность прямых при продолжительности процесса 2…6 час. Это позволяет вычислить для данного временного интервала средний угловой коэффициент, который равен –6413, и кажущуюся энергию активации: . Кстати, кажущаяся энергия активации, найденная для всего временного интервала 1…8 час, равна 127,5 кДж и мало отличается от 122,6 кДж.