В ходе решения различных квалиметрических задач на практике широко используются экспертные методы оценки качества, которые в совокупности с измерительными методами позволяют получить наиболее полный объем информации об объекте исследования.В связи с этим на начальном этапе любой экспертизы основной задачей квалиметролога является грамотное формирование экспертной группы, в ходе которого определяется оптимальное количество экспертов, необходимое для проведения экспертизы, а также проводится количественная оценка качества экспертной группы различными методами.
Расчет количества экспертов необходимого для выявления наиболее полного количества данных сводится к нахождению такого их числа m, при котором вероятность появления содержательно нового предложения с привлечением (m+1) –го эксперта становится меньше заранее принятого значения α.
Для решения поставленной задачи используют следующий алгоритм [10]:
1. Проводят опрос экспертов с целью получения совокупности сведений, касающихся объекта экспертизы.
2. Все предложения экспертов разделяют на четыре группы:
1) очевидные – выдвинутые всеми экспертами;
2) известные – выдвинутые большинством экспертов, но не всеми;
3) неочевидные – выдвинутые меньшинством;
4) особые – выдвинутые одним экспертом.
Интерес представляют только неочевидные и особые предложения, базирующиеся на личном опыте экспертов, их способностях, интуиции. При этом вероятность появления особых предложений среди всех предложений, выдвинутых меньшинством в группе из m экспертов, определяется по выражению
 , (1)
, (1)
где 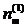 - количество особых предложений;
- количество особых предложений;
 , …
, … 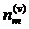 - количества неочевидных предложений, выдвинутых меньшинством.
- количества неочевидных предложений, выдвинутых меньшинством.
3. Из группы в m экспертов образуют всевозможные подгруппы по (m-1) экспертов и для каждой из них подсчитывают число особых  и неочевидных
и неочевидных  предложений.
предложений.
4. Рассчитывают вероятность 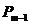 появления особых предложений по всем подгруппам и коэффициент λ уменьшения вероятности появления особых предложений с переходом от (m-1) экспертов к m экспертам:
появления особых предложений по всем подгруппам и коэффициент λ уменьшения вероятности появления особых предложений с переходом от (m-1) экспертов к m экспертам:
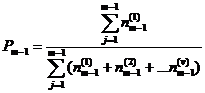 , (2)
, (2)
 . (3)
. (3)
5. При условии, что значение λ сохраняется с увеличением количества экспертов (хотя, как правило, оно при этом уменьшается), оценки вероятности появления особых предложений с привлечением (m+1) – го, (m+2) -го…, (m+k) -го экспертов будут соответственно равны:
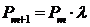 ; (4)
; (4)
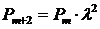 ; (5)
; (5)
…
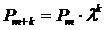 . (6)
. (6)
Используя выражения (3), (6) и заданное значение вероятности α, находят число k вновь привлекаемых экспертов, при котором 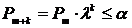 . Окончательная формула для расчета k примет вид:
. Окончательная формула для расчета k примет вид:
 .
.
Следует отметить, что все допущения рассмотренного способа решения ориентированы на расчет «с запасом», т.е. считая всех экспертов одинаково продуктивными, мы заведомо шли на завышение требуемого количества экспертов. В действительности (при правильно проведенном отборе экспертов) вначале в экспертную группу попадают наиболее сведущие специалисты, которые представляют максимальную информацию.
Привлекаемые далее эксперты менее продуктивны уже потому, что область их профессиональных интересов удаляется от цели проведения экспертизы. Это приводит к уменьшению λ.
Так как рассмотренный вариант решения дает завышенный объем экспертной группы, превышать рассчитанное количество экспертов не целесообразно. Главное – подробно опросить каждого эксперта, выявить наиболее полно его суждения и рационально организовать обмен мнениями.
Пример расчета количества экспертов.
При индивидуальном анкетном опросе группа из пяти экспертов в результате генерации подала 26 предложений, относящихся к объекту экспертизы, некоторые из которых по содержанию совпадают друг с другом [11]. При этом все предложения можно разделить в соответствии с предложенной выше классификацией:
очевидные -  ;
;
известные - 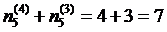 ;
;
неочевидные - 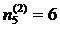 ;
;
особые - 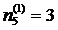 .
.
Требуется определить сколько еще экспертов k следует опросить, чтобы вероятность 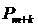 появления содержательно нового предложения стала меньше α=0,05.
появления содержательно нового предложения стала меньше α=0,05.
Решение.
Находим оценку вероятности появления особых предложений среди всех предложений, выдвинутых меньшинством, в группе из m=5 экспертов:
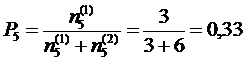 .
.
Образуем теперь из группы экспертов всевозможные подгруппы по четыре эксперта (этих подгрупп будет пять) и для каждой из них подсчитаем число особых 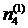 и неочевидных
и неочевидных  предложений. Нетрудно убедиться, что эти числа будут 4, 4, 4, 3, 2 и 6, 4, 2, 6, 6. Следовательно, оценка вероятности появления особых предложений в группе из четырех экспертов будет
предложений. Нетрудно убедиться, что эти числа будут 4, 4, 4, 3, 2 и 6, 4, 2, 6, 6. Следовательно, оценка вероятности появления особых предложений в группе из четырех экспертов будет
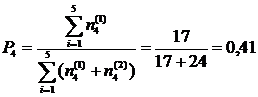 .
.
По найденным значениям  и
и  найдем коэффициент λ, а также заданного значения α рассчитываем количество k вновь привлекаемых экспертов по формуле (7):
найдем коэффициент λ, а также заданного значения α рассчитываем количество k вновь привлекаемых экспертов по формуле (7):
 .
.
Итак, для достижения поставленного условия следует привлечь к работе еще 9 специалистов, или всего 14 человек.
Задание
Вариант 0
Таблица 1.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,05 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | + | Известные | |||
| + | + | + | |||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 1
Таблица 2.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,05 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | + | Известные | |||
| + | + | + | + | ||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 2
Таблица 3.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,1 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | + | Известные | |||
| + | + | + | |||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 3
Таблица 4.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,1 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | + | Известные | |||
| + | + | + | + | ||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 4
Таблица 5.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,05 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | + | Известные | |||
| + | + | + | + | ||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 5
Таблица 6.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,05 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | Известные | ||||
| + | + | + | + | ||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 6
Таблица 7.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,1 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | + | Известные | |||
| + | + | + | |||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 7
Таблица 8.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,1 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | Известные | ||||
| + | + | + | |||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 8
Таблица 9.
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,05 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | Известные | ||||
| + | + | + | |||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |
Вариант 9
Таблица 10
Исходные данные для определения количества экспертов
| Номер предложения | Номер эксперта | Вид предложения | α | ||||
| + | + | + | + | + | Очевидные | 0,05 | |
| + | + | + | + | + | |||
| + | + | + | + | + | |||
| + | + | + | + | Известные | |||
| + | + | + | + | ||||
| + | + | + | |||||
| + | + | Неочевидные | |||||
| + | + | ||||||
| + | + | ||||||
| + | Особые | ||||||
| + | |||||||
| + |