Метод конечных элементов
Метод конечных элементов можно рассматривать с двух позиций: с «инженерной» и математической (вариационной).
Первое, «инженерное» направление активно развивалось в период становления метода специалистами по строительной механике и представляет собой обобщение основных методов строительной механики стержневых систем на случай сплошных тел. Еще в 1933 году проф. И.М.Рабинович высказал мысль о возможности и эффективности использования методов строительной механики стержневых систем в теории упругости. Однако осуществление этой идеи стало возможным лишь с появлением ЭВМ.
В МКЭ сплошное тело представляется как система из подобластей достаточно малых, но конечных размеров, называемых конечными элементами. Конечные элементы связаны между собой в отдельных точках, называемых узлами. Зная жесткостные характеристики конечных элементов и эквивалентные узловые силы, получаемые в результате приведения объемных и поверхностных нагрузок к узлам системы, можно для сплошного тела применить методы строительной механики стержневых систем. Наибольшее распространение приобрел вариант МКЭ в форме метода перемещений.
Второе направление развивалось математиками - специалистами в области вариационных методов. Здесь МКЭ представляется как вариационно-разностный метод, а именно: метод Ритца с локализованными базисными функциями, для построения которых рассчитываемая область покрывается сеткой. Базисные функции выбираются таким образом, чтобы они были не равными нулю лишь на небольшой части области вблизи рассматриваемого узла, а на остальной части области принимали нулевые значения. Вследствие этого, большая часть базисных функций будет ортогональна друг другу, и многие коэффициенты разрешающей системы уравнений обратятся в нуль. Матрица системы уравнений получается редкозаполненной, что позволяет применить для ее решения методы разреженных матриц. При определенных способах нумерации узлов структура матрицы системы уравнений принимает удобный для численного решения вид (рис.1). Существуют специальные методы перенумерации неизвестных, позволяющие уменьшить ширину ленты матрицы.
При использовании данного подхода нет необходимости представлять, что элементы соединяются только в узлах. Базисные функции для каждого конечного элемента можно выбрать так, что непрерывность перемещений по граням стыковки элементов между собой удовлетворяется автоматически. Такие конечные элементы называются совместными.
Заметим, что во всех случаях матрица системы разрешающих уравнений является симметричной, что позволяет хранить в памяти ЭВМ только верхнюю половину ленты матрицы. Это обстоятельство является очень важным, так как в практических расчетах порядок матрицы часто достигает нескольких тысяч.
|
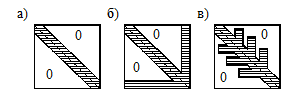
Рис.1. Структура матрицы системы разрешающих уравнений в МКЭ: а) ленточная,
б) ленточная с окаймлением, в) типа «небоскреба».
Впоследствии выяснилось, что «инженерный» (прикладной) и математический подходы представляют собой разные точки зрения на один и тот же метод, оба подхода сблизились, и резкая грань между ними исчезла. Тем не менее в литературе существуют описания МКЭ, тяготеющие к одной из указанных точек зрения. Ниже приводится далеко не полный перечень книг по МКЭ.
Описания МКЭ с прикладной точки зрения:
1. Сегерлинд Л. Применение метода конечных элементов. М.: Мир, 1979. 392с.
2. Розин Л.А. Метод конечных элементов. Л., 1971.
3. Розин Л.А. Основы метода конечных элементов в теории упругости. Л.: Изд-во ЛПИ, 1972. 77с.
4. Постнов В.А., Хархурим И.Я. Метод конечных элементов в расчетах судовых конструкций. Л.: Судостроение, 1974. 342с.
5. Розин Л.А. Стержневые системы как системы конечных элементов. Л.: Изд-во ЛГУ, 1975. 237с.
6. Зенкевич О.К. Метод конечных элементов в технике. М.: Мир, 1975. 542с.
7. Постнов В.А. Метод суперэлементов. Л., 1979.
Описание МКЭ с математической точки зрения:
1.Стренг Г., Фикс Дж. Теория метода конечных элементов. М.: Мир, 1977. 350с.
2. Оден Дж. Конечные элементы в нелинейной механике сплошных сред. М., 1976.
3. Бате К., Вилсон Е. Численные методы анализа и метод конечных элементов. М.: Стройиздат, 1982. 448с. (эту книгу можно отнести также и к выше приведенному списку).
Большой вклад в развитие МКЭ и внедрение его в практику расчетов внесли советские ученые В.Г.Корнеев, А.Р.Ржаницын, Л.А.Розин, А.С.Сахаров, В.А.Постнов, Н.Н.Шапошников и др.
Для расчета конструкций МКЭ разработано множество программных комплексов. Перечислим некоторые из них (данные 80-х г.г. прошлого века).
Отечественные комплексы:
1. «Прочность» - КИСИ (БЭСМ-6, ЕС ЭВМ).
2. «Спринт» (система прочностных расчетов института
транспорта) - МИИТ (ЕС ЭВМ).
3. «ЛИРА» (линейный расчет) - НИИАСС Госстроя УССР.
4. «SCAD» - НИИАСС Госстроя УССР.
5. «Феникс» (нелинейный расчет) - НИИАСС Госстроя УССР.
6. «Мираж» (суперэлементный расчет) - НИИАСС
Госстроя УССР.
7. «Каскад» и «Каскад-2» - Ленинградский кораблестроительный институт.
8. «Фронт» - Киевский механический завод.
9. «Диана» - Московский механический завод «Опыт».
Зарубежные комплексы:
1. «ASAS» - фирма «Atcin & Partners» (США).
2. «EASE» - фирма «Engineering Analysis»
(Великобритания).
3. «STARDYNE» - фирма «Mechanics Research» (США).
4. «STRUDL» - Массачусетский технологический
институт (США).
5. «NASTRAN» - NASA (США).
6. «MARS-STRUS» - фирма IBM (США).
7. «ASKA» - Штутгардский университет (Германия).
8. «COSAR» - Высшая техническая школа (г.Магдебург,
Германия).
9. «SESAM» - Норвежский технический институт.