Синтез одноконтурных САР

Синтез систем автоматизации и управления

 

Задача синтеза САУ - задача определения оптимального (в смысле некоторого критерия качества) управления. В качестве критериев качества управления могут выступать максимум производительности (максимум быстродействия), минимум себестоимости, минимум энергетических затрат,

требуемое качество продукции и др. Поскольку, как правило, невозможно в результате синтеза получить экстремальные значения всех критериев качества функционирования системы, приходится выбирать в качестве основного тот или иной критерий, либо решать задачу многокритериального синтеза с учетом весовых коэффициентов при отдельных критериях качества.

Ниже рассмотрены типовые методы улучшения качественных показателей САУ без привлечения оптимизационных процедур синтеза, а также вопросы структурно-параметрического синтеза простейших электромеханических САУ на основе минимизации интегрально-квадратических критериев качества.

 

 

Типовые методы улучшения динамических показателей

Систем автоматизации и управления.

 

Прежде, чем перейти к оптимизационным процедурам синтеза САУ,

рассмотрим, что лежит в основе традиционных подходов к задачам повышения качественных показателей автономных динамических систем регулирования. В идеальном случае динамическая погрешность отработки сигнала задания в САР должна быть равна нулю. На самом деле, ограничения, накладываемые на ресурсы управления, вынуждают искать некий компромисс, в частности - между временем регулирования и перерегулированием выходной координаты. При этом наиболее часто прибегают к одному из двух подходов.

 

Форсирование управляющего воздействия.

Этот способ позволяет очень эффективно снизить динамическую

T ВГ.

ошибку регулирования в простейших САР. В качестве примера рассмотрим процесс регулирования тока возбуждения генератора постоянного тока. На рис. 8.1. приведены функциональная схема (а) объекта управления и переходные процессы (б) напряжения и тока возбуждения без форсирования и с форсированием управляющего воздействия. Тиристорный возбудитель (ТВ) представлен безынерционным звеном, цепь тока возбуждения – апериодическим звеном 1-го порядка. Эквивалентная постоянная времени цепи возбуждения принята равной

 

 

Кривая 1 – реакция тока возбуждения на ступенчатое задающее воздействие без форсировки управляющего водействия, кривая 2 - реакция тока возуждения на то же самое задающее воздействие с

двухкратной форсировкой управляющего воздействия. Форсировка осуществляется кратковременно на время t _рег1, при котором ток возбуждения достигает заданного значения. Заметим, что форсирование сигнала управления позволяет в несколько раз снизить время регулирования и существенно уменьшить динамическую ошибку регулирования, однако далеко не всегда осуществимо. В частности, в рассмотренном примере тиристорный возбудитель для реализации двухкратной форсировки должен иметь соответствующий запас по напряжению, а, следовательно, запас по углу отпирания тиристоров. К недостаткам этого метода следует отнести необходимость применения нетиповых корректирующих звеньев (релейного элемента и компаратора).

 

Компенсация больших постоянных времени объекта

Управления.

Выполняется после структурно-параметрической декомпозиции объекта управления. Допустим, в результате структурной декомпозиции выделен объект управления, структурная схема которого приведена на рис. 8.2.

 

 

 

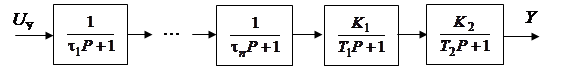Рис. 8.2. Структурная схема выделенного из среды автономного

объекта управления

 

Этот объект управления содержит 2 апериодических звена 1-го порядка с большими постоянными времени (БПВ) T ₁ и T ₂ и n звеньев с малыми постоянными времени (МПВ) t₁ … t _n, причем t _i << T ₁, T ₂, i = 1… n. Тогда, учитывая, что произведением МПВ можно пренебречь, запишем выражение для эквивалентной МПВ:

 

 

Эту постоянную времени часто называют некомпенсированной малой постоянной времени, поскольку, во-первых, компенсации подлежат только БПВ, во-вторых, любая технически реализуемая САУ после компенсации всех БПВ все равно будет обладать некоторой инерцией и именно эта некомпенсированная МПВ будет определять быстродействие системы.

Таким образом, параметрическая декомпозиция ОУ приводит к замене всех звеньев с МПВ одним эквивалентным звеном

 

.

 

Установим на входе ОУ компенсирующее (корректирующее) ПИД – звено

 

.

 

Тогда, передаточная функция объекта управления со звеном компенсации (разомкнутого контура регулирования)

 

 

Как видим ОУ существенно упростился и синтез оптимального управления им уже не представляет сложностей (см. следующий раздел). В замкнутой САР корректирующее звено целесообразно включить в структуру регулятора.

Заметим, что все сказанное справедливо лишь в случае идеальной компенсации БПВ объекта управления. В действительности параметры ОУ всегда рассчитываются (оцениваются) с некоторой погрешностью, при функционировании САР претерпевают температурные, временные и прочие изменения. Параметры компенсирующего звена также могут подвергаться температурному, временному дрейфу. Все это приводит к недокомпенсации или перекомпенсации БПВ и, как следствие, к снижению эффекта от компенсации. Кроме того, компенсация довольно больших постоянных времени требует соответствующих затрат энергии, а реальные ограничения, накладываемые на энергетические ресурсы, приводят к сужению зоны малых отклонений координат ОУ, т.е. к нелинейности САР. Тем не менее, данный метод улучшения динамических показателей широко применяется в сочетании с процедурами синтеза оптимальных систем управления.

 

Синтез одноконтурных САР

Любой автономный контур регулирования САУ необходимо стремиться настроить оптимально в смысле желаемого критерия качества регулирования. В линейных САР настройка контуров регулирования практически оказывается компромиссной, и чаще всего это компромисс между быстродействием и колебательностью. При этом замкнутый контур регулирования по сути дела представляет собой оптимальный в смысле заданного критерия качества фильтр с некоторым коэффициентом передачи.

В теории и практике синтеза САУ наибольшее распространение получили оптимальные фильтры Баттерворта (Боттерворса), Башарина, Бесселя, Чебышева, Калмана, Хемминга и др. / 3 /.

В электромеханических САУ, например в системах управления электроприводами, настройку контуров регулирования осуществляют, как правило, в соответствии с фильтрами Баттерворта того или иного порядка. В качестве критериев качества регулирования (критериев оптимизации) здесь выступают интегральные квадратические критерии. Для фильтров Баттерворта 1…4 порядков эти критерии записываются в виде:

где T _m - малая некомпенсированная постоянная времени объекта

управления,

Передаточные функции замкнутых контуров регулирования,

соответствующие фильтрам Баттерворта 1 … 4 порядков имеют вид:

где K _ос – коэффициент обратной связи контура регулирования.

Заметим, что по мере увеличения порядка контура регулирования корни характеристических полиномов уменьшаются в геометрической прогрессии, а следовательно снижается быстродействие контуров.

Переходные функции h (t _*) соответствующих контуров регулирования имеют вид:

где t_* - относительное время, t_* = t / T_m.

На рис. 8.3. приведены переходные процессы в контурах регулирования, синтезированных в соответствие с фильтрами Баттерворта 1…4 порядка.

Для подавляющего большинства САУ перерегулирование выходной координаты не должно превышать 10 – 20 % в диапазоне малых отклонений координат, т.е. в линейной зоне. Заметим, что для фильтров Баттерворта перерегулирование не превышает 8%.