При решении линейных уравнений с параметром
сначала его нужно привести к виду, удобному для исследования
(стандартный канонический вид линейного уравнения с параметром),
выполнив ряд преобразований, потом следует определить контрольные
значения параметра, т.е. те значения, при которых коэффициент при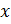 
обращается в ноль. Эти значения разбивают множество значений параметра
на несколько множеств, которые необходимо исследовать.
III. Примеры простейших линейных уравнений с параметром
1. 
Ответ: при 
корней нет, при 
2. 
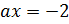
Ответ: при корней нет, при 
3. 
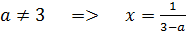
Ответ: при 
корней нет,
при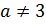 
.
4. 
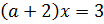
Ответ: при 
корней нет,
при 
.
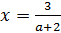5. 
Ответ: при 
корней нет,
при 
.
6. 
Ответ: при 
при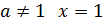 
7. 
Ответ: при 
при 
8. 
Ответ: при 
при 
9. 
Ответ: при 
при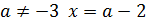 
10. 
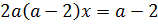
1) 
2) 
3) 
Ответ: если , то корней нет
если 
, 
если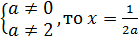 
11. 
т. е.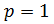 
и 
контрольные значения параметра.
1) При 
2) 
3) При 
Ответ: если , то корней нет
если 
,
если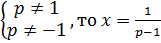 
IV. Линейные уравнения с параметром, имеющие стандартный канонический вид
– стандартный канонический вид линейного уравнения с параметром
Пример 1:
Ответ: если 
если 
Пример 2:
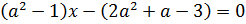
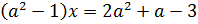
При 
При 
Ответ: при 
при 
при 
Пример 3:
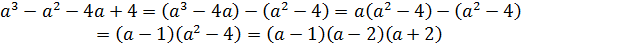
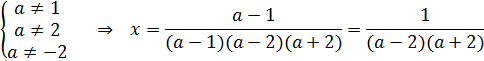
Ответ: при 
при 
при 
V. Уравнения, приводимые к линейным уравнениям с параметром
Схема решения уравнений, приводимых к линейным:
1) Указать и исключить все значения параметра и переменной, при которых уравнение теряет смысл.
2) Умножить обе части уравнения на общий знаменатель, не равный нулю.
3) Привести уравнение-следствие к виду 
и решить его.
4) Исключить значения параметра, когда найденный корень принимает значения, при которых уравнение теряет смысл.
5) Записать ответ.
6)
Пример 1:
контрольное значение параметра.
1) При 
=> 
=> x – любое число
2) При 
Ответ: при 
при 
Пример 2:
1) 
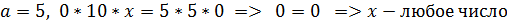
2) 
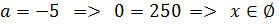
3) 
Ответ: при 
, корней нет
если 
,
при 
Примеры решений уравнений, содержащих параметр в знаменателе:
Пример 1:
ОДЗ: 
при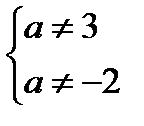 
Ответ: при 
решений нет;
при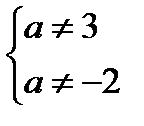 
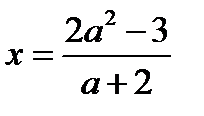
Пример 2:
Умножим уравнение на 
:
Ответ: при 
при 
при 
Пример 3:
ОДЗ: 
При 
Ответ: При 
нет решений
При x 
Пример 4:
Умножим уравнение на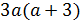 
:
Ответ: при 
при 
при 
Примеры решений уравнений, содержащих и параметр и переменную в знаменателе
Пример 1:
Умножим уравнение на 
:
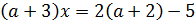
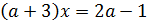
Исключим те a, при которых 
:
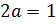
Ответ: при 
при
при 
Пример 2:
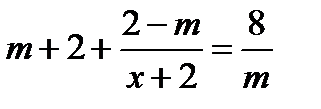
=> при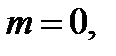 
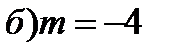
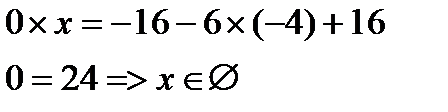
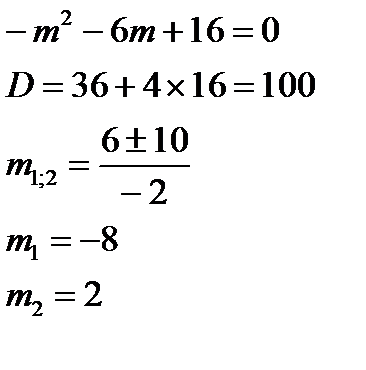
г)Найдём m при 
:
Ответ: Если 
Если 
x-любое
Если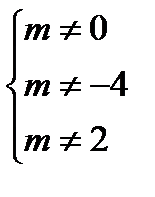 
Пример 3:
При m=1 не имеет смысла
При 
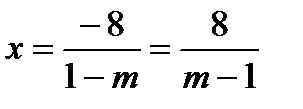
Найдём m при которых 
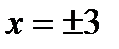
Ответ: при 
уравнение не имеет смысла
При 
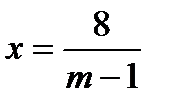
Заключение
В заданиях ГИА и ЕГЭ постоянно встречаются линейные уравнения и неравенства с параметрами. Познакомившись с подобными уравнениями, мы заинтересовались этой темой. Разбираться и решать эти уравнения было очень интересно и познавательно.
Мы изучили общий принцип и метод решений линейных уравнений с параметром, рассмотрели различные виды уравнений и научились их решать.
Надеемся, что наша научная работа поможет нам и нашим сверстникам в решении трудных задач.
Список использованной литературы:
1.Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре 8-9. М.: Просвещение, 2001.
2.Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. М.; Харьков: Илекса; Гимназия, 2003.
3.Полякова Е.А. Уравнения и неравенства с параметрами. М.: Илекса; 2010.
4.Шахмейстер А.Х. Уравнения и неравенства с параметрами. СПб.; «Петроглиф»,2006.