Способы задания множеств. Операции над множествами.
Основные соотношения алгебры множеств.
Цель работы: изучение способов задания множеств. Приобретение практических навыков в выполнении операций над множествами и проверке основных соотношений алгебры множеств.
Теоретическая справка
Множество - объединение в одно целое различимых между собой элементов.
Конечное множество - множество, состоящее из конечного числа элементов.
Бесконечное множество - множество, состоящее из бесконечного числа элементов.
Способы задания множеств
1) Перечисление элементов.
Например:
А = {1,3,5,6,889,-10}
2) Задание определяющего свойства.
Например:
X = { x | 1 > х > 5, x є Z };
А = { a2 | a - четное число}.
Пустое множество – множество, не содержащее ни одного элемента. Пустое множество обозначается Æ.
Универсальное – множество, содержащее все возможные элементы. Универсальное множество обозначается U.
Утверждение " а является элементом множества А " записывается в виде а Î А (а принадлежит множеству А).
Утверждение " а не является элементом множества А " записывается в виде а Ï А (а не принадлежит множеству А).
Множества А и В называются равными (обозначается А = В), если они состоят из одних и тех же элементов.
Если каждый элемент множества А является также элементом множества В, то говорят, что А содержится или включается в В. В этом случае пишут А Í В.
Множество A называется подмножеством множества B,если A Í B.
В тех случаях, когда одновременно имеют место соотношения A Í B и A ¹ B, говорят, что A строго включается в B, и используют запись A Ì B.
Операции над множествами
Объединением множеств A и B (обозначается A È B) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств, т.е
A È B = { а ½ а Î A или а Î B }.
Пересечением множеств A и B (обозначается A Ç B) называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств, т.е.
А Ç B = { а ½ а Î А и а Î B }.
Разностью множеств А и B (обозначается А \ B) называется множество, состоящее из всех элементов множества A, не принадлежащих множеству B, т.е.
А \ B ={ а ½ а Î А и а Ï B }.
Дополнением множества А в универсальном множестве U (обозначается  , ØА) называется множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству А, т.е.
, ØА) называется множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству А, т.е.
ØА = U \ A
Симметрической разностью множеств A и B (обозначается A Å B или A D B) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.
A D B = { а ½ либо а Î A и а Ï B, либо а Ï A и а Î B }
A D B = (A \ B) È (B \ A) = (A È B) \ (A Ç B)
Операции над множествами можно проиллюстрировать графически с помощью кругов Эйлера (их также называют диаграммами Венна). В этом случае исходные множества изображают кругами, а множество-результат выделяют штриховкой.
 |
Основные законы алгебры множеств:
1) Коммутативные законы
А È В = В È А
А Ç В = В Ç А
А D В = В D А
2) Ассоциативные законы
А È (В È С) = (А È В) È С
А Ç (В Ç С) = (А Ç В) Ç С
3)Дистрибутивные законы
А È (В Ç С) = (А È В) Ç (А È С)
А Ç (В È С) = (А Ç В) È (А Ç С)
4)Законы с Æ и U
А È Æ = А А Ç U = А А È  = U
= U
А Ç Æ = Æ А È U = U А Ç  = Æ
= Æ
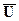 = Æ
= Æ  = U
= U
6) Законы идемпотентности
А Ç А = А А È А = А  = А
= А
7) Законы поглощения
А È (А Ç В) = А А È ( Ç В) = А È В
Ç В) = А È В
А Ç (А È В) = А А Ç ( È В) = А Ç В
È В) = А Ç В
8) Законы де Моргана
______
A Ç B =  È
È 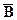
_______
A È B =  Ç
Ç 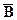
9) Законы склеивания
(А Ç В) È ( Ç В) = В
Ç В) = В
(А È В) Ç ( È В) = В
È В) = В
Справедливость законов алгебры множеств доказывается на основе определения равенства: Х = Y, если
1) Х Í Y:" x Î X Þ x Î Y;
2) Y Í Х:" y Î Y Þ y Î X.
Сформулированный принцип называют интуитивным принципом объемности.
Для доказательств будем использовать следующие обозначения ({ - и; [ - или) и соотношения:
x Î A Ç B Þ  x Î A È B Þ
x Î A È B Þ 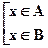
x Ï A Ç B Þ  x Ï A È B Þ
x Ï A È B Þ 
x Î A \ B Þ  x Ï A \ B Þ x Ï A Ç
x Ï A \ B Þ x Ï A Ç 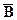 Þ
Þ 
Например:
Используя отношения принадлежности, доказать тождество
(A D B) \ C = (A \ C) D (B \ C).
Пусть X = (A D B) \ C;
Y = (A \ C) D (B \ C).
Если x Î X Þ x Î (A D B) \ C Þ
 Þ
Þ  Þ
Þ 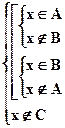 Þ
Þ  Þ
Þ 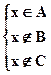 или
или  .
.
Если y Î Y Þ y Î (A \ C) D (B \ C) Þ
y Î [(A \ C) \ (B \ C)] È [(B \ C) \ (A \ C)] Þ  Þ
Þ 
 |

 Þ
Þ 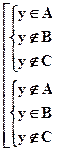 Þ
Þ  или
или  .
.
Отсюда  или
или  =
=  или
или  .
.
Следовательно тождество верно.