По определению степени с натуральным показателем степень an представляет собой произведение n множителей, каждый из которых равен a. Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел, можно получить и обосновать следующие свойства степени с натуральным показателем:
1. основное свойство степени am·an=am+n, его обобщение an1·an2·…·ank=an1+n2+…+nk;
2. свойство частного степеней с одинаковыми основаниями am:an=am−n;
3. свойство степени произведения (a·b)n=an·bn, его расширение (a1·a2·…·ak)n=a1n·a2n·…·akn;
4. свойство частного в натуральной степени (a:b)n=an:bn;
5. возведение степени в степень (am)n=am·n, его обобщение (((an1)n2)…)nk=an1·n2·…·nk;
6. сравнение степени с нулем:
o если a>0, то an>0 для любого натурального n;
o если a=0, то an=0;
o если a<0 и показатель степени является четным числом 2·m, то a2·m>0, если a<0 и показатель степени есть нечетное число 2·m−1, то a2·m−1<0;
7. если a и b – положительные числа и a<b, то для любого натурального n справедливо неравенство an<bn;
8. если m и n такие натуральные числа, что m>n, то при 0<a<1 выполняется неравенство am<an, а при a>0 справедливо неравенство am>an.
Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an.
Теперь рассмотрим каждое из них подробно.
1. Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют основным свойством степени: для любого действительного числа a и любых натуральных чисел m и n справедливо равенство am·an=am+n.
Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида am·an можно записать как произведение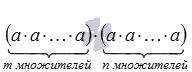 
. В силу свойств умножения полученное выражение можно записать как 
, а это произведение есть степень числа a с натуральным показателем m+n, то есть, am+n. На этом доказательство завершено.
|
|
Приведем пример, подтверждающий основное свойство степени. Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3, по основному свойству степени можно записать равенство 22·23=22+3=25. Проверим его справедливость, для чего вычислим значения выражений 22·23 и 25. Выполняя возведение в степень, имеем 22·23=(2·2)·(2·2·2)=4·8=32 и 25=2·2·2·2·2=32, так как получаются равные значения, то равенство 22·23=25 - верное, и оно подтверждает основное свойство степени.
Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n1, n2, …, nk справедливо равенство an1·an2·…·ank=an1+n2+…+nk.
Например, (2,1)3·(2,1)3·(2,1)4·(2,1)7=(2,1)3+3+4+7=(2,1)17.
2. Можно переходить к следующему свойству степеней с натуральным показателем – свойству частного степеней с одинаковыми основаниями: для любого отличного от нуля действительного числа a и произвольных натуральных чисел m и n, удовлетворяющих условию m>n, справедливо равенство am:an=am−n.
Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0n=0, а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени am−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m<n), а мы ведем разговор про свойства степени с натуральным показателем.
|
|
Доказательство. Основное свойство дроби позволяет записать равенство am−n·an=a(m−n)+n=am. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями.
Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2, рассмотренному свойству степени отвечает равенство π5:π2=π5−3=π3.
3. Теперь рассмотрим свойство степени произведения: натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней an и bn, то есть, (a·b)n=an·bn.
Действительно, по определению степени с натуральным показателем имеем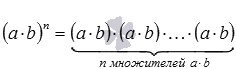 
. Последнее произведение на основании свойств умножения можно переписать как 
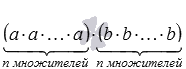, что равно an·bn.
Приведем пример: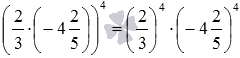 
.
Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a1·a2·…·ak)n=a1n·a2n·…·akn.
Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем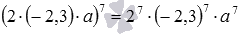 
.
|
|
4. Следующее свойство представляет собой свойство частного в натуральной степени: частное действительных чисел a и b, b≠0 в натуральной степени n равно частному степеней an и bn, то есть, (a:b)n=an:bn.
Доказательство можно провести, используя предыдущее свойство. Так (a:b)n·bn=((a:b)·b)n=an, а из равенства (a:b)n·bn=an следует, что (a:b)n является частным от деления an на bn.
Запишем это свойство на примере конкретных чисел: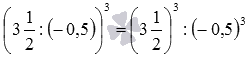 
.
5. Теперь озвучим свойство возведения степени в степень: для любого действительного числа a и любых натуральных чисел m и n степень am в степени n равна степени числа a с показателем m·n, то есть, (am)n=am·n.
Например, (52)3=52·3=56.
Доказательством свойства степени в степени является следующая цепочка равенств: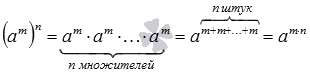 
.
Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p, q, r и s справедливо равенство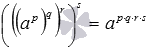 
. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
6. Осталось остановиться на свойствах сравнения степеней с натуральным показателем.
Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.
Для начала обоснуем, что an>0 при любом a>0.
Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a. Эти рассуждения позволяют утверждать, что для любого положительного основания a степень an есть положительное число. В силу доказанного свойства 35>0, (0,00201)2>0 и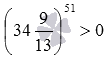 
.
Достаточно очевидно, что для любого натурального n при a=0 степень an есть нуль. Действительно, 0n=0·0·…·0=0. К примеру, 03=0 и 0762=0.
Переходим к отрицательным основаниям степени.
Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m, где m - натуральное. Тогда 
. По правилу умножения отрицательных чисел каждое из произведений вида a·a равно произведению модулей чисел a и a, значит, является положительным числом. Следовательно, положительным будет и произведение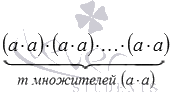 
и степень a2·m. Приведем примеры: (−6)4>0, (−2,2)12>0 и 
.
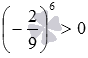Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1, то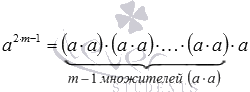 
. Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5)3<0, (−0,003)17<0 и 
.
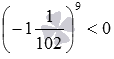7. Переходим к свойству сравнения степеней с одинаковыми натуральными показателями, которое имеет следующую формулировку: из двух степеней с одинаковыми натуральными показателями n меньше та, основание которой меньше, а больше та, основание которой больше. Докажем его.
Неравенство an<bn представляет собой произведение левых и правых частей n верных неравенств a<b, следовательно, в силу свойств неравенств справедливо и доказываемое неравенство вида an<bn. Например, в силу этого свойства справедливы неравенства 37>(2,2)7 и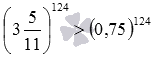 
.
8. Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.
Докажем, что при m>n и 0<a<1 выполняется неравенство am<an. Для этого запишем разность am−an и сравним ее с нулем. Записанная разность после вынесения an за скобки примет вид an·(am−n−1). Полученное произведение отрицательно как произведение положительного числа an и отрицательного числа am−n−1 (an положительна как натуральная степень положительного числа, а разность am−n−1 отрицательна, так как m−n>0 в силу исходного условия m>n, откуда следует, что при 0<a<1 степень am−n меньше единицы). Следовательно, am−an<0 и am<an, что и требовалось доказать. Для примера приведем верное неравенство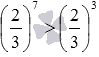 
.
Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо am>an. Разность am−an после вынесения an за скобки принимает вид an·(am−n−1). Это произведение положительно, так как при a>1 степень an есть положительное число, и разность am−n−1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень am−n больше единицы. Следовательно, am−an>0 и am>an, что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 37>32.