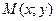|
в ней. Перенесем начало координат в точку 
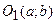, не изменяя направления осей. Получим новую систему координат 
О1 ХУ. Выразим Х, У через х, у. При любом расположении точек будем иметь: ОА + АР = ОР, где ОА = а, ОР = х, АР = Х. аналогично для У:
ПОВОРОТ ОСЕЙ КООРДИНАТ
Дана прямоугольная система координат О ху и точка 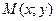в ней. Для получения новой системы повернем оси на угол α: 
. Используя свойства проекций, получим:
ОБЩИЕ ФОРМУЛЫПРЕОБРАЗОВАНИЯ
Найдем взаимосвязь между координатами 
и 
точки М в системе координат О ху и О1 ХУ, полученной одновременно и сдвигом, и поворотом осей. Введем вспомогательную систему координат 
. Тогда
; 
ОБЩЕЕ УРАВНЕНИЕ ЛИНИИ ВТОРОГО ПОРЯДКА
Общее уравнение кривой второго порядка обычно записывают в виде
. (1)
Удвоенные обозначения используются потому, что во многие формулы входят половины соответствующих коэффициентов. Составим два определителя:
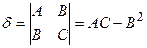и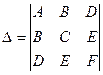 
.
В зависимости от значений Δ (большой дискриминант) и δ (малый дискриминант) уравнение (1) определяет следующий геометрический образ:
| δ | Δ ≠ 0 | Δ = 0 |
| δ > 0 | Эллипс (действительный или мнимый) | Точка |
| δ < 0 | Гипербола | Пара пересекающихся прямых |
| δ = 0 | Парабола | Пара параллельных прямых (действительных или мнимых) |
Линии второго порядка, имеющие единственный центр (эллипс, гипербола, пара пересекающихся прямых), называются центральными. Линии второго порядка, имеющие множество центров или вовсе их не имеющие (парабола, пара параллельных прямых), называются нецентральными. Таким образом, для центральных кривых δ ≠ 0, для нецентральных кривых δ = 0.
ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ КРИВОЙ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ
Преобразование уравнения (1) к одному из простейших видов выполняют по следующей схеме:
А) Предварительное преобразование. С его помощью освобождаются от члена, содержащего произведение координат. Это достигается поворотом осей координат О х и О у на угол α, который находится по формуле 
. Формулы преобразования
.
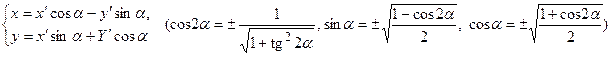Члены с 
взаимно уничтожаются, и новое уравнение будет иметь вид
Б) Завершающее преобразование. С его помощью освобождаются от слагаемых, содержащих первые степени координат. Вид кривой и расположение её на плоскости легко устанавливаются преобразованием уравнения к виду 
(в случае 
и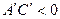 
). Затем переносом начала координат в точку 
уравнение приводится к каноническому виду. В случае 
(т.е. либо 
, 
, либо 
, 
) уравнение определит параболу, которая может вырождаться в две параллельные прямые.
Преобразование уравнения центральной линии к простейшему виду рекомендуется начинать с переноса начала координат в центр. Координаты точки определяют из системы уравнений
С помощью параллельного переноса 
уравнение (1) преобразуется к виду
,
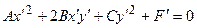где 
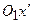. Затем поворотом осей 
и 
на угол α, определяемый по формуле , последнее уравнение приводится к каноническому виду 
.