Дано:
Шифр периодического сигнала s1 ─ 4 из табл. 3[1];
Рис. 1
После подстановки значений параметров и масштабирования, получаем:
Рис. 2
Длительность периода ─ Т = 0,001 с = 1000 мкс;
Соотношение между периодом и длительностью импульса ─ Т = 3τ
Соотношение параметров цепи и сигнала:
Шифр цепи – 2 из табл. 4[1];
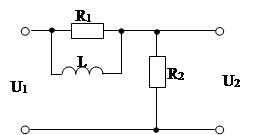
Рис. 3
Значения сопротивлений из табл. 1[1] – R1 = 2R; R2 = R
Задание:
Рассчитать и построить в масштабе АЧХ и ФЧХ интегрирующей и дифференцирующей цепей в диапазоне от нуля до 10 кГц, полагая 
(по шкале абсцисс сделать градуировку частоты в кГц и в безразмерных величинах wtц);
Рассчитать и построить в масштабе переходную и импульсную характеристики цепей от нуля до tmax = 3tц (по шкале абсцисс сделать градуировку времени в мкс и в безразмерных величинах t/tц);
Проверить выполнение предельных соотношений между частотными и импульсными характеристиками.
Рассчитать спектр амплитуд и фаз на выходе заданной цепи при действии периодического сигнала s1(t).
Построить с учетом масштаба на общей спектрограмме спектры амплитуд и фаз входного и выходного сигналов при действии сигнала s2(t).
Дать представление входного сигнала с помощью функций Хевисайда.
Получить динамическое представление отклика заданной цепи на действие сигнала s2(t)(с помощью переходных характеристик).
Изобразить отклик цепи на интервале времени от нуля до tmax, в три раза превышающем длительность воздействия сигнала s2(t).
Сделать выводы по результатам проведенного анализа.
Расчет частотных характеристик интегрирующей и дифференцирующей цепей.
Выполнение пунктов 1-3 задания оформляем в виде таблицы.
Табл. 1 – Анализ дифференцирующей и интегрирующей цепей.
| Дифференцирующая цепь | Интегрирующая цепь |
Рис. 4
| 
Рис. 5
|
| 
|
| 
|
Вводим оператор дифференцирования р, такой, что 
| |
Передаточный коэффициент цепи:
| 
Передаточный коэффициент цепи:
|
| Находим комплексный передаточный коэффициент, заменяя р на jw | |
| 
|
После анализа цепей находим частотные характеристики.
Табл. 2 – Частотные характеристики цепей
| Дифференцирующая цепь | Интегрирующая цепь | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Амплитудно-частотная (АЧХ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фазочастотная (ФЧХ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 6. АЧХ ДЦ
| 
Рис. 7. АЧХ ИЦ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
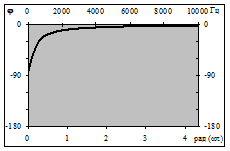Рис. 8. ФЧХ ДЦ
| 
Рис. 9. ФЧХ ИЦ
|
Расчет временных характеристик дифференцирующей и интегрирующей цепей.
Находим временные характеристики операторным методом, пользуясь значением операторного коэффициента найденного в пункте 1.
Табл. 3 – Временные характеристики цепей
| Дифференцирующая цепь | Интегрирующая цепь | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Импульсные | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Переходные | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 10. ИХ ДЦ
| 
Рис. 11 ИХ ИЦ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 12. ПХ ДЦ
| 
Рис. 13. ПХ ИЦ
|
Проверка соотношений между частотными и временными характеристиками дифференцирующей и интегрирующей цепей.
Предельные соотношения
Табл. 4 – Предельные соотношения
| Дифференцирующая цепь | Интегрирующая цепь |
| 
|
| 
|
Расчет спектра амплитуд и фаз на выходе заданной цепи при действии периодического сигнала s1(t).
По известной формуле из теории четырехполюсников находим передаточный коэффициент заданной цепи:
Находим комплексный передаточный коэффициент, заменяя р на jw
Найдем спектральную плотность непериодического сигнала на входе(s2(t)) и выходе (s2в(t)) цепи, соответствующему периодическому сигналу s1(t) на протяжении одного периода.
Спектральная плотность непериодического сигнала s2(t)(см. к.р.№1):
Спектральную плотность выходного сигнала s2в(t) найдем по формуле:
Учитывая, что
и 
,
а также 
Учитывая, что: 
или 
, получаем:
Спектр амплитуд выходного периодического сигнала s1В(t):
Спектр фаз:
Табл. 6 – Спектры входного и выходного периодического сигналов
| n | 
| 
| 
| 
|
| A0=|ao/2|=0,667 | A0=|ao/2|=0,667 | 1,04575 | ||
| 0,551 | 0,361 | -0,162 | ||
| 0,276 | 0,130 | -0,152 | ||
| – | – | |||
| 0,138 | -1 | 0,054 | -1,102 | |
| 0,110 | -1 | 0,042 | -1,085 | |
| – | – | |||
| 0,079 | 0,029 | -0,063 | ||
| 0,069 | 0,026 | -0,055 | ||
| – | – | |||
| 0,055 | -1 | 0,021 | -1,045 |
Построение спектров амплитуд и фаз входного(s2(t)) и выходного(s2в(t)) непериодического сигналов
В соответствии с пунктом 2, имеем:
Амплитудные спектры
Учитываем, что при w=0
Амплитуда – четная функция частоты
Фазные спектры
Где функция sign(w)=1 при w>0 и sign(w)=-1 при w<0
Фаза – нечетная функция частоты
Табл. 7 – Спектры входного и выходного непериодического сигналов
| 
| 
| 
| 
|
| -10 | 0,0276 | 0,0094 | 1,04575 | |
| -9,75 | – | – | ||
| -9,375 | 0,0184 | 0,0063 | 0,048648 | |
| -9 | – | – | ||
| -8,625 | 0,0200 | 0,0068 | 1,052634 | |
| -8,25 | – | – | ||
| -7,5 | 0,0849 | 0,0294 | 0,059951 | |
| -6,75 | – | – | ||
| -6,375 | 0,0270 | 0,0095 | 1,069491 | |
| -6 | – | – | ||
| -5,625 | 0,0306 | 0,0109 | 0,077593 | |
| -5,25 | – | – | ||
| -4,5 | 0,1415 | 0,0518 | 1,093529 | |
| -3,75 | – | – | ||
| -3,375 | 0,0510 | 0,0199 | 0,115996 | |
| -3 | – | – | ||
| -2,625 | 0,0656 | 0,0275 | 1,135528 | |
| -2,25 | – | – | ||
| -1,5 | 0,4244 | 0,2259 | 0,164845 | |
| -0,75 | – | – | ||
| -0,375 | 0,4594 | 0,4151 | 1,096523 | |
| 0,6667 | – | 0,6667 | – | |
| 0,375 | 0,4594 | -1 | 0,4151 | -1,096523 |
| 0,75 | – | – | ||
| 1,5 | 0,4244 | 0,2259 | -0,164845 | |
| 2,25 | – | – | ||
| 2,625 | 0,0656 | -1 | 0,0275 | -1,135528 |
| – | – | |||
| 3,375 | 0,0510 | 0,0199 | -0,115996 | |
| 3,75 | – | – | ||
| 4,5 | 0,1415 | -1 | 0,0518 | -1,093529 |
| 5,25 | – | – | ||
| 5,625 | 0,0306 | 0,0109 | -0,077593 | |
| – | – | |||
| 6,375 | 0,0270 | -1 | 0,0095 | -1,069491 |
| 6,75 | – | – | ||
| 7,5 | 0,0849 | 0,0294 | -0,059951 | |
| 8,25 | – | – | ||
| 8,625 | 0,0200 | -1 | 0,0068 | -1,052634 |
| – | – | |||
| 9,375 | 0,0184 | 0,0063 | -0,048648 | |
| 9,75 | – | – | ||
| 0,0276 | -1 | 0,0094 | -1,04575 |
Рис. 14 – Амплитудный спектр входного и выходного периодического сигналов.
Рис. 15 – Фазовый спектр входного и выходного непериодического сигналов.
Представление входного непериодического s2(t) с помощью единичной функции s(t) (функции Хевисайда).
Входной сигнал является суммой функций Хевисайда, сдвинутых по временной оси и умноженных на амплитуду сигнала Е.
Рис. 16 – Функции Хевисайда
Динамическое представление отклика заданной цепи на действие сигнала s2(t).
Заданная цепь является суммой интегрирующего и дифференцирующего звеньев.
Находим переходную характеристику заданной цепи
Так как переходная функция является откликом цепи на единичный сигнал, то воспользовавшись линейностью преобразований Лапласа, получаем отклик заданной цепи на непериодический сигнал s2(t).
, где
Динамическое представление отклика:
Табл. 8 – Отклик заданной цепи на действие непериодического сигнала
| t/T | -1/2-0 | -1/2+0 | -1/3 | -1/6-0 | -1/6+0 | 1/6-0 | 1/6+0 | 1/3 | 1/2-0 | 1/2+0 | 2/3 | 5/6 | 7/6 | 4/3 | 3/2 | 5/3 | 11/6 | |||
| -0,33307 | -0,6912 | -0,84558 | -0,85702 | -0,9338 | -0,9669 | -0,96935 | -0,98581 | -0,9929 | -0,99343 | -0,99696 | -0,99859 | -0,99935 | -0,9997 | -0,99986 | -0,99994 | -0,99997 | -0,99999 | -1 | |
| 0,33328 | 0,6913 | 0,845627 | 0,857068 | 0,933821 | 0,966905 | 0,969358 | 0,985812 | 0,993431 | 0,996958 | 0,998592 | 0,999348 | 0,999698 | 0,99986 | 0,999935 | |||||
| -0,33335 | -0,69133 | -0,84564 | -0,85708 | -0,93383 | -0,96936 | -0,98581 | -0,99343 | -0,99696 | -0,99859 | -0,99935 | -0,9997 | -1 | |||||||
| 0,333729 | 0,691508 | 0,857164 | 0,933865 | 0,969379 | 0,985822 | 0,993435 | 0,99696 | 0,998593 | |||||||||||
| -0,33307 | -0,6912 | -0,84558 | -0,52374 | -0,2425 | -0,12127 | -0,44563 | -0,74332 | -0,87164 | -0,54743 | -0,25347 | -0,11736 | -0,05434 | -0,02516 | -0,01165 | -0,00539 | -0,0025 | -0,00116 |
Рис. 17 – Изображение входного непериодического сигнала s2 и отклик цепи на него.
Выводы.
Анализ линейной цепи облегчается, тем, что передаточный коэффициент заданной цепи можно представить в виде линейной комбинации передаточных коэффициентов интегрирующей и дифференцирующей цепей.
В этом случае можно достаточно просто находить отклик цепи на сигнал, представляя его как линейную комбинацию откликов элементарных цепей.
При прохождении сигнала через линейную цепь нули и точки экстремума его амплитудного и фазного спектров не меняются. Меняется лишь само значение экстремумов амплитудного спектра.
Представление прямоугольно импульсных сигналов с помощью функции Хевисайда позволяет достаточно просто рассчитать отклик цепи, как линейную комбинацию откликов на единичную функцию включения.
Операторный метод и теория обобщенных функций дает достаточно мощный аппарат для исследования цепей и сигналов.
Контрольная работа №3