Дано:
Шифр входного сигнала s(t) ─ N1= 4; N2= 3 из табл. 2[1];
N2= 3 – Соотношение параметров импульса: t2 = 1,5t1 из табл. 5[1];
N1= 4 – Номер рисунка из табл. 5[1] – 4;

Рис. 1
Шифр цепи – N3 N4= 44 из табл. 3[1];
Номер рисунка из табл. 6[1] N3 N4= 44;

Рис. 2
Соотношение параметров цепи и сигнала:

Задание:
Рассчитать и построить в масштабе АЧХ и ФЧХ цепи
Рассчитать и построить в масштабе переходную и импульсную характеристики цепи;
Проверить выполнение предельных соотношений между частотными и импульсными характеристиками.
Дать поинтервальное аналитическое представление сигнала по его графику;
Рассчитать операторным методом или методом временного интегрирования отклик на выходе линейной цепи и дать его поинтервальное описание
По результатам вычислений изобразить отклик на выходе линейной цепи на отрезке времени от нуля до tmax, в три раза превышающем длительность воздействия сигнала. Сигнал воздействия и отклика совместить на одном рисунке.
Сделать выводы (оценка операторного и временного методов применительно к решаемой задаче, физическая интерпретация полученных результатов).
Расчет частотных характеристик линейной цепи второго порядка
Для того, чтобы найти операторную передаточную функцию, преобразуем схему

Рис. 3
Согласно известной из теоретической электротехники формуле переходим от треугольника к эквивалентной звезде:

Рис. 4
На холостом ходу:

Рис. 5
Находим операторный передаточный коэффициент:

Находим корни знаменателя К(р)

Получаем

Получаем комплексный передаточный коэффициент заменяя р на jw

АЧХ цепи: 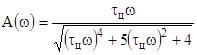
ФЧХ цепи: 
Табл. 1 – Расчет АЧХ и ФЧХ цепи
| f,кГц | 0,80 | 1,59 | 2,25 | 3,18 | 4,77 | 7,96 | 15,92 | 31,83 | ¥ | |
| w,рад/с | 14142,14 | ¥ | ||||||||
| wtц,рад | 0,5 | 
| ¥ | |||||||
| К(w) | 0,22 | 0,32 | 0,33 | 0,32 | 0,26 | 0,18 | 0,10 | 0,05 | ||
| j(w) | 900 | 49,400 | 18,430 | 0,000 | -18,430 | -37,870 | -56,890 | -72,980 | -81,430 | -900 |

Рис. 6 – АЧХ цепи второго порядка

Рис. 7 – ФЧХ цепи второго порядка
Расчет временных характеристик линейной цепи второго порядка
Временные характеристики находим по обратному преобразованию Лапласа, используя операторный передаточный коэффициент. Операторный коэффициент является суммой коэффициентов интегрирующих звеньев вида


Импульсная характеристика интегрирующей цепи (см. к.р.№2)

Переходная характеристика интегрирующей цепи (см. к.р.№2)

Импульсная характеристика заданной цепи:

Переходная характеристика заданной цепи:

Табл. 2 – Расчет временных характеристик
| t,мкс | 69,315 | ||||||||||
| t/ τц | 0,1 | 0,2 | 0,5 | 0,6 | 0,69315 | 0,8 | |||||
| h(t) | 7326,2 | 5219,1 | 1292,3 | 535,8 | 0,0 | -455,4 | -972,1 | -448,3 | -66,5 | -0,5 | |
| g(t) | 0,000 | 0,086 | 0,148 | 0,239 | 0,248 | 0,250 | 0,247 | 0,233 | 0,047 | 0,007 | 0,000 |

Рис. 8 – Импульсная характеристика цепи

Рис. 9 – Переходная характеристика цепи
Предельные соотношения между частотными и временными характеристиками.

Поинтервальное описание входного сигнала
Обозначим длительность сигнала – Т.
Тогда


Рис. 10 – Входной сигнал
На интервале t=[0; 0,4T] 
На интервале t=[0,4T; 0,6T] 
На интервале t=[0,6T; T] 
Используя функцию включения можно записать представление входного сигнала в виде:

Расчет отклика на выходе цепи
Рассчитываем отклик на выходе методом временного интегрирования, используя интеграл Дюамеля:



На интервале t=[0; 0,4T]

На интервале t=[0,4T; 0,6T]

На интервале t=[0,6T; T]

На интервале
t=[T; ¥]  , где:
, где:

Найдем отклик операторным методом. Входной сигнал равен:
 .
.
Пользуясь преобразованием Лапласа
 ,
,



Обратное преобразование по Лапласу выражений вида:

Обратное преобразование по Лапласу выходного сигнала:

Окончательно:

На интервале t=[0; 0,4T]

На интервале t=[0,4T; 0,6T]

На интервале t=[0,6T; T]

На интервале t=[T; ¥]
 ,
,
Построение графика отклика сигнала на выходе цепи
Табл. 3 – Расчет отклика сигнала
| t, мкс | ||||||||||||||||
| t/T | 0,2 | 0,4 | 0,6 | 0,8 | 1,2 | 1,4 | 1,6 | 1,8 | 2,2 | 2,4 | 2,6 | 2,8 | ||||
| Sв(t) | 0,077 | 0,200 | 0,224 | 0,097 | -0,080 | -0,147 | -0,125 | -0,089 | -0,059 | -0,038 | -0,023 | -0,014 | -0,009 | -0,005 | -0,003 |

Рис. 11 – Входной и выходной сигналы
Выводы
Проделанная работа показывает, что с помощью функций Хевисайда можно представлять не только прямоугольные импульсы, но и сигналы более сложной формы. В этом случае можно перейти от кусочной аппроксимации к аналитическому изображению сигналов с точки зрения теории обобщенных функций.
Сравнение временного и операторного методов для нахождения отклика заданной цепи говорит в пользу последнего, так как операторный метод позволяет более полно охватывать процесс вычислений и является более емким.
Отклик на входной сигнал данной цепи второго порядка является апериодическим, так как корни знаменателя операторного передаточного коэффициента действительные.
По графику отклика можно судить об интегрирующей природе цепи.