Глава 5. Сопряженные пространства и сопряженные операторы.
Пусть 
- комплексное банахово пространство, 
- линейный ограниченный оператор, для любого 
рассмотрим линейный ограниченный оператор 
,
,
.
Определение 1. Значение 
называется регулярное значение оператора 
, если для оператор 
обратимый, то есть существует линейный ограниченный оператор 
.
Множество всех регулярных значений оператора называется резольвентным и обозначается 
. Оно объединяет только те значения параметра , при которых оператор является обратимым. Резольвентное множество делит комплексную плоскость на две части:
- резольвентное множество
- те значения , при которых является необратимым оператором.
Определение 2. Спектр 
оператора называется множество всех тех , для которых оператор не имеет обратного.
Следовательно множество 
представимо в виде дизъюнктивного непересекающегося объединения резольвентного множества и спектра оператора
.
Необратимость оператора может быть следствием разных причин. Например, ядро нетривиально или образом является не все пространство, соответственно вводится классификация точек спектра.
Рассмотрим основные свойства спектра и резольвентного множества.
Теорема 1. для любого линейного ограниченного оператора резольвентное множество является открытым неограниченным множеством.
Доказательство. По утверждению данной теоремы спектр, как дополнение оказывается замкнутым множеством.
Пусть произвольно фиксированный линейный ограниченный оператор. Докажем, что неограниченное множество. Резольвенте принадлежит внешность (множество вне).
{круг радиуса равного 
, 
}
Это и означает неограниченность резольвенты. Зафиксируем , такое что 
.
Докажем, что 
обратим (это и означает, что элемент 
)). Воспользуемся теоремой 3 об обратимости.
Пусть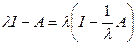 
. Обратимость этого оператора следует из условия 
или 
.
Для доказательства открытости зафиксируем 
и покажем что вместе с некоторой своей окрестностью, это и означает открытость множества. , следовательно оператор 
является обратимым.
Пусть 
. Так как первое слагаемое является обратимым оператором, следовательно, сумма тоже является обратимым оператором по теореме 4, если норма второго слагаемого удовлетворяет неравенству:
,
Так как 
, следовательно 
. Обозначим через 
- радиус окружности с центром в 
и, продолжение окружности является открытой окрестностью с центром в , следовательно доказали, что - открытое множество.
Приведем представление обратного оператора в виде ряда Неймана: 
Вернемся к рассмотрению спектра оператора. Воспользуемся тем, что спектр является дополнением резольвенты до всей комплексной плоскости.
Теорема 2. Спектр любого ограниченного линейного оператора является:
- не пустым;
- замкнутым;
- ограниченным множеством.
Доказательство.
Доказательство того, что спектр не пустое множество опустим.
Замкнутость следует из того, что резольвента открытое множество, следовательно, дополнение открытого множества замкнуто.
Из доказательства теоремы 1 следует, что спектр 
(кругу радиуса равного 
), следовательно, спектр ограниченное множество.
В зависимости от причины необратимости оператора спектр подразделяется на три взаимно непересекающихся подмножества.
-
- (точечный спектр) содержит только те значения , при которых ядро оператора нетривиально. То есть 
следовательно 
, уравнение при данном имеет хотя бы одно ненулевое решение. Такое значение называется собственным, а соответствующие элементы собственными, следовательно, точечный спектр - это объединение всех собственных значений данного оператора. -
- (непрерывный спектр) содержит те , которые не принадлежат точечному спектру. То есть 
, но образ оператора является всюду плотным в . -
- (остаточный спектр) содержит те , которые не попали ни в точечный спектр, ни в непрерывный спектр. То есть и 
не всюду плотно в .
Следовательно, справедливо дизъюнктивное представление:
.
Одна или более компонент может быть не пустыми, но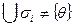 
.
Для вполне непрерывных операторов спектр имеет достаточно простую структуру, аналогично структуре матричного оператора в алгебре (любой матричный оператор в 
- мерном Евклидовом пространстве имеет ровно собственных чисел с учетом кратности, то есть 
).
Теорема 3. Спектр вполне непрерывного ограниченного оператора содержит не более чем счетное множество собственных значений с единственно возможной предельной точкой 
.
Утверждение теоремы 3 можно записать в виде 
. Теорема 3 устанавливает примерные границы спектра произвольного оператора.
Спектральный радиус – радиус линейного круга с центром в , содержащего в себе спектр данного оператора и обозначается 
.
Для точного или приблизительного вычисления спектрального радиуса воспользуемся формулой
.
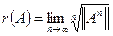Спектральный радиус может быть и нулем.