Изучение этого раздела следует начать с изучения механизма трех элементарных видов теплообмена: теплопроводности, конвекции и излучения.
Слушатель должен усвоить закон Фурье, понятия: температурное поле, изотермическая поверхность, температурный градиент, разобраться в физической сущности коэффициента теплопроводности.
В результате изучения темы «Стационарная теплопроводность» слушатель должен научиться определять тепловой поток, передаваемый через однослойную и многослойную плоскую стенки, а также стенку полого цилиндра (трубы) и стенку полого шара.
В условиях пожара теплообмен носит нестационарный характер, поэтому слушатель должен уяснить вывод дифференциального уравнения теплопроводности, усвоить сущность краевых условий при решении теплотехнических задач, овладеть методикой расчета температурного поля в плоской стенки, сплошном цилиндре и полуограниченном теле при заданных граничных условиях.
Конвективный теплообмен, как известно из опыта, зависит от многих факторов. Например, условий движения жидкости, её физических свойств и др. Изучается он в основном экспериментально с использованием теории гидродинамического и теплового подобия. Слушатель должен хорошо представлять сущность теории подобия и усвоить, как методы подобия используются при изучении вопросов конвективного теплообмена.
Необходимо овладеть методикой расчета конвективного теплообмена при различных случаях движения теплоносителя. Запоминать конкретные эмпирические уравнения не нужно, но необходимо уметь рассчитывать числа подобия: Нуссельта Nu, Грасгофа Gr, Рейнольдса Re, Прандтля Pr.
Рассматривая теплообмен при изменении агрегатного состояния,следует уяснить физическую природу уменьшения коэффициента теплоотдачи во время перехода от пузырькового режима кипения к пленочному и опасность работы кипятильных устройств при пленочном режиме.
Изучая теплообмен при конденсации пара, нужно обратить внимание на необходимость учета этого явления при проектировании и эксплуатации установок пожаротушения.
При пожарах значительная часть тепловой энергии от горящих тел окружающим предметам передается излучением. Необходимо изучить основные законы лучистого теплообмена и овладеть методикой расчета тепловых потоков излучения, а также методикой расчета безопасных расстояний. Ознакомиться с особенностями излучения и поглощения газов.
Под теплопередачей понимают сложный процесс теплообмена. Этот процесс происходит в теплообменных аппаратах. Следует уяснить классификацию теплообменных аппаратов по принципу действия, уметь рассчитывать температурный напор при различных схемах течения теплоносителей, овладеть методикой расчета теплообменных аппаратов по соображениям пожарной безопасности.
При изучении тепло и массообмена необходимо усвоить сущность процесса и разобраться в расчетных экспериментальных уравнениях.
В практике пожарного дела важно уметь рассчитывать температурный режим при пожаре в помещении. Поэтому необходимо овладеть методикой расчета температурного режима.
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА №1
Стационарные процессы
Контрольная работа №1 состоит из 2-х теоретических вопросов и 3-х расчетных задач. Теоретические вопросы выбираются по таблице 1.4.
Теоретические вопросы к контрольной работе №1
- Почему в качестве рабочих тел тепловых двигателей используются газы?
2. Будет ли правильным утверждение, что всё тепло, подводимое к газу, обуславливает изменение его температуры?
- Как доказать, что количество тепла Q есть функция процесса, а не состояния тела?
- Может ли работа необратимого процесса быть больше работы обратимого процесса?
5. Можно ли среднюю теплоёмкость вычислить по формуле: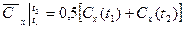 
, где 
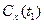и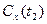 
- истинные теплоёмкости.
6. Как вычисляется и почему не зависит от характера процесса изменение внутренней энергии тела?
- Может ли процесс подвода тепла сопровождаться уменьшением температуры?
8.
|
-
Известна комбинация термодинамических процессов
для 1 кг воздуха в P-V координатах. Построить эту 2 3
комбинацию процессов в T-S координатах и определить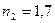 
знаки работы, теплоты и изменения внутренней энергии
в процессе 3-1.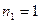 
|
-
Есть ли разница в понятиях необратимый и неравновесный процесс? - Почему у реальных веществ при изотермическом расширении q неравно L?
12. Как вычислить объёмную теплоёмкость смеси газов, заданную массовыми долями, и массовую теплоёмкость смеси, заданную объёмными долями?
- В чём эквивалентность различных формулировок второго начала термодинамики?
- Можно ли теплоту некоторого источника полностью превратить в работу?
- Как изменяется энтропия рабочего тела при его расширении в пустоту?
- Может ли энтропия системы убывать в необратимых процессах?
- Система релаксирует к состоянию равновесия. Что происходит с её энтропией?
- Как можно вычислить значение энтропии воздуха при заданных давлении и температуре?
- Обладает ли энтропией электрический ток?
20. Каково значение цикла Карно в термодинамике? Покажите, что в данном интервале температур от Т1 до Т2 цикл Карно самый экономичный.
21. Какая существует связь между изменением энтропии и потерей работоспособности тела в необратимых процессах? Какую роль на потери работоспособности оказывает температура теплоприёмника (Тmin)?
- В чём состоит ошибочность вывода о тепловой смерти вселенной?
23. Покажите, что в Т-S координатах в области перегретого пара изобара большего давления располагается выше изобары меньшего давления.
- Является ли полным дифференциалом величина:
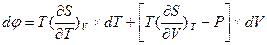? - Покажите, что две изобары в Т-S координатах не пересекаются друг с другом.
- Вычислите интеграл:
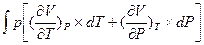,при условии P=const. - Докажите, что для реальных газов
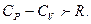
28. Выведите уравнение для вычисления изменения внутренней энергии газа, подчиняющегося уравнению состояния Ван-дер-Ваальса.
- Найдите величину свободной энергии реального газа.
- Существуют ли термодинамические потенциалы у неравновесных систем?
- Обладает ли тепло трения эксергией?
- Показать в диаграмме T-S эксергетические потери в двух последовательных процессах.
| |||
 | |||
2
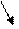i =const q=0
 |
|
- Может ли выполняться неравенство
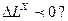
- Может ли эксергия принимать отрицательные значения?
35. Почему нельзя взять в качестве независимых переменных давление и температуру для двухфазной системы?
- Покажите на диаграмме T-S энтальпию перегретого пара.
37. В каком случае для расчёта изотермического процесса можно воспользоваться формулой изобарного процесса?
- Что происходит с теплотой парообразования с увеличением давления?
39. Какая система называется гомогенной и гетерогенной? Дайте примеры той и другой системы.
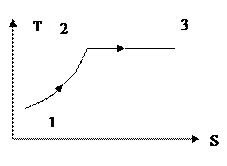
- Рабочее тело совершает процессы,
изображенные на диаграмме T-S. Покажите графически эксергию теплоты.
Для выполнения работы необходимо изучить по учебнику (1) в соответствии с программой раздел «Основы термодинамики реальных процессов» и стационарные процессы раздела «Основы тепло и массообмена».
Задача 1.1. Параметры смеси газов. Истечение газов
В помещении компрессорной станции объемом V произошла разгерметизация трубопровода, по которому транспортируется горючий газ под давлением P1 при температуре Т1. через образовавшееся в трубопроводе сквозное отверстие площадью f газ выходит в помещение.
Рассчитать, через какое время τ во всем объеме компрессорной станции может образоваться взрывоопасная смесь, а также среднюю молекулярную массу, плотность, удельный объем и изобарную удельную массовую теплоемкость смеси, если ее температура Т = 293 К, а давление Р = 100 кПа. Коэффициент расхода отверстия ξ = 0,7. воздухообмен не учитывается.
Данные, необходимые для расчетов, приведены в таблице 1.1.
Таблица 1.1
| Последняя цифра шифра | ||||||||||
| V∙10-2,м3 f∙10 4,м2 | 4,2 | 5,9 | 5,0 | 2,0 | 5,1 | 4,1 | 5,0 | 6,0 | 4,2 | 1,5 |
| Предпоследняя цифра шифра | ||||||||||
| Р1, МПа Т1, К | 0,7 | 0,5 | 0,5 | 1,5 | 1,0 | 1,5 | 0,2 | 0,4 | 0,2 | 0,9 |
| Газ | Бутан | Этан | Пропан | Метан | Этилен | Водород | Бутилен | Ацетилен | Аммиак | Пропилен |
Задача 1.2. Конвективный теплообмен. Теплопередача
Рукавная линия диаметром d поперечно обдувается воздухом со скоростью ωв. Температура воздуха tв. По рукавной линии со скоростью ωж движется вода, температура которой на входе в рукавную линию t'ж. рассчитать максимальную длину рукавной линии из условия, чтобы температура на выходе из рукавной линии была t''ж ≥ 10С. Толщина стенки рукавной линии δ = 4мм. эквивалентный коэффициент теплопроводности материала рукава принять λ = 0,115 Вт/(м∙К).
Данные, необходимые для расчетов, приведены в таблице 1.2.
Таблица 1.2
| Последняя цифра шифра | ||||||||||
| ωв, м/с tв, 0С | -50 | -40 | -30 | -20 | -50 | -40 | -30 | -20 | -10 | -50 |
| Предпоследняя цифра шифра | ||||||||||
| ωж, м/с t'ж, 0С d, мм | 3,2 | 1,6 | 4,2 | 2,8 | 3,8 | 2,0 | 3,5 | 1,05 | 2,4 | 1.0 |
Задача 1.3. Лучистый теплообмен
Определить минимальное расстояние, обеспечивающее безопасность соседнего с горящим объекта, при исходных данных: проекция факела пламени горящего объекта имеет прямоугольную форму размером d ∙ l, его температура Тф, а степень черноты εф. На поверхности не горящего объекта: допустимое значение температуры Тдоп, допустимое значение плотности теплового потока (критическая плотность) qкр, степень черноты поверхности ε.
Кроме того, оценить безопасное расстояние от факела для личного состава, работающего на пожаре без средств защиты, от теплового воздействия при условии: а) кратковременного пребывания; б) длительной работы. При кратковременном тепловом воздействии для кожи человека qкр = 1120 Вт/м2, при длительном qкр = 560 Вт/м2. При решении задачи учитывать только теплообмен излучением. Коэффициент безопасности принять равным β. Данные, необходимы для расчета приведены в таблице 1.3.
Таблица 1.3
| Последняя цифра шифра | ||||||||||
| d, м l, м Тф∙10-2, К εф | 0,8 | 0,7 | 0,6 | 0,4 | 0,7 | 0,6 | 0,8 | 0,4 | 0,7 | 0,6 |
| Предпоследняя цифра шифра | ||||||||||
| Тдоп, К ε qкр∙10-2 Вт/м2 β | 0,9 1,8 | 0,9 1,7 | 0,85 1,6 | 0,8 1,5 | 0,85 1,4 | 0,8 1,3 | 0,7 1,4 | 0,7 1,5 | 0,6 1,6 | 0,6 1,7 |
Таблица 1.4
таблица теоретических вопросов
| Последняя цифра зачётной книжки. | |||||||||||
| Предпоследняя цифра З.К. | |||||||||||
| 1; 21 | 2; 22 | 3;23 | 4; 24 | 5; 25 | 6; 26 | 7; 27 | 8; 28 | 9; 29 | 10; 30 | ||
| 11; 31 | 12; 32 | 13; 33 | 14; 34 | 15; 35 | 16; 36 | 17; 37 | 18; 38 | 19; 39 | 20;40 | ||
| 10,30 | 11,31 | 12,32 | 13,33 | 14,34 | 15,35 | 16,36 | 17,37 | 18,38 | 19,39 | ||
| 11;21 | 12; 22 | 13; 23 | 14;24 | 15; 25 | 16; 26 | 17; 27 | 18; 28 | 19; 29 | 20;30 | ||
| 1; 31 | 2; 32 | 3; 33 | 4; 34 | 5; 35 | 6; 36 | 7; 37 | 8; 38 | 9; 39 | 10,40 | ||
| 20;40 | 19;39 | 18;38 | 17;37 | 16; 36 | 15; 35 | 14; 34 | 13; 33 | 12; 32 | 11;31 | ||
| б | 10;30 | 9;29 | 8;28 | 7;27 | 6;26 | 5;25 | 4;24 | 3;23 | 2;22 | 1;21 | |
| 11; 40 | 12; 39 | 13; 38 | 14; 37 | 15; 36 | 16; 35 | 17; 34 | 18; 33 | 19; 32 | 20; 31 | ||
| 1; 30 | 2; 29 | 3; 28 | 4; 27 | 5; 26 | 6; 25 | 7; 24 | 8; 23 | 9; 22 | 10; 21; | ||
| 1;40 | 18;10 | 2;31 | 6;17 | 21;15 | 18;33 | 22;44 | 5;22 | 11;15 | 33;12 |
Контрольная работа №2
Нестационарные процессы
Контрольная работа №2 состоит из 2-х теоретических вопросов и 3-х расчетных задач. Теоретические вопросы выбираются по таблице 2.3.
Теоретические вопросы к контрольной работе №2
1.Объясните, почему есл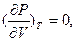и 
то и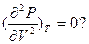 
Каков геометрический смысл критической точки?
2.Покажите, что при температуре абсолютного нуля теплота перехода одной конденсированной фазы в другую равняется нулю.
3.Изобразите на диаграммах P-V и T-S графики, соответствующие изотермическому, изобарическому и изохорическому процессам вещества, свойства которого описываются уравнением Ван-дер-Ваальса.
4.Почему изотермы перегретого пара постепенно переходят в горизонтальные прямые в i-S диаграмме?
5.Как можно по стандартной диаграмме i-S, где отсутствует нижняя пограничная кривая, определить энтальпию кипящей воды и скрытую теплоту парообразования?
6.Как определить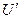 
и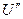 
для вычисления внутренней энергии влажного пара по формуле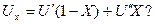 
7.Можно ли получить перегретый пар в изотермическом процессе?
8.Изобразите в T-S диаграмме располагаемую работу при истечении газа и пара через сопло.
9.Только ли с помощью сопла Лаваля можно осуществить непрерывный переход от дозвуковых к сверх звуковым скоростям? Укажите примеры.
10.Какова будет скорость истечения воздуха через суживающееся сопло по отношению к скорости звука, если перед соплом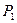 
= 10 бар, а за соплом 
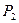=3 бар.
11.Какое сечение сопла называют критическим?
12.Что произойдёт с располагаемым теплоперепадом, если газ перед соплом подвергнуть дросселированию?
13.Можно ли скорость истечения пара рассчитать по уравнению:
?
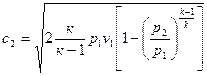14.Может ли коэффициент адиабатического дросселирования быть равным коэффициенту обратимого адиабатического расширения? Если да, то, при каких условиях это возможно?
15.Можно ли перегреть влажный пар, подвергнув его адиабатическому дросселированию?
16.Может ли увеличиваться внутренняя энергия газа при его дросселировании?
17.Какая существует разница между процессами адиабатического и изотермического дросселирования?
18.Выгоден ли процесс дросселирования с точки зрения энергетики?
19.Зачем применяют многоступенчатое сжатие в компрессорах?
20.Какая разница между индикаторной и теоретической диаграммами поршневого компрессора?
21.Как влияют на экономичность цикла поршневого двигателя внутреннего сгорания с подводом тепла при V=const степень сжатия и свойства рабочего тела?
22.В чём состоит смысл и значение регенерации тепла в газотурбинных установках?
23.Что экономичнее: газотурбинная установка или двигатель внутреннего сгорания при одинаковом подводе тепла?
24.Для чего в воздушно-реактивных двигателях применяют турбокомпрессоры? Как выглядит экономичность этих двигателей по отношению к прямоточным реактивным двигателям?
25.Почему в современных паросиловых установках используется цикл Рэнкина, а не цикл Карно?
26.Всегда ли использование вторичного перегрева пара повышает экономичность паросиловой установки?
27.Почему регенерация тепла в паросиловых установках осуществляется не так, как в газотурбинных установках?
28.Почему при характеристике теплофикационных установок для оценки экономичности их работы недостаточно знания одного термического КПД установки?
29.Почему не целесообразно применять воздушные поршневые холодильные установки и почему применение турбокомпрессорных холодильных установок является разумным?
30.Какие основные требования предъявляются к холодильным агентам паровых холодильных установок и почему?
31.Какова разница понятий: холодильный эффект теплоносителя и холодильный коэффициент? Как их определить?
32.В чём состоит разница понятий: абсолютная влажность воздуха и относительная влажность воздуха?
33.Почему в расчётах с влажным воздухом энтальпию его всегда относят к 1 кг сухого воздуха?
34.Как с помощью диаграммы i-d влажного воздуха определить энтальпию сухого и насыщенного влажного воздуха при температуре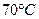 
?
35.Установите зависимость концентрации водорода, растворяющегося в металле в виде атомов Н, от давления водорода.
36.Напишите выражение закона действующих масс для следующих реакци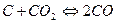й: 
и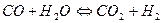 
37.Сколько независимых параметров определяет состояние равновесной смеси жидкого и газообразного азота? Сравните химические потенциалы этих двух подсистем.
38.Сопровождаются ли работой фазовые переходы типа жидкость-пар?
39Применимо ли понятие химического потенциала к газу, в котором не протекают химические реакции?
40.Применимо ли правило фаз Гиббса к механическим системам?
Для выполнения работы необходимо изучить по учебнику в соответствии с программой в разделе «Основы тепло и массообмена» нестационарные процессы. Обратить особое внимание на материал, излагаемый в § 25.2, 16.3, 18.4 и 17.1.
Задача 2.1. Температурный режим при пожаре в помещении
Производство, связанное с обращением ГЖ, размещено в помещении размерами в плане a*b, м. и высотой Н, м. при аварии технологических аппаратов возможны и розлив жидкости на пол и возникновение пожара. Предусмотрены устройства, ограничивающие растекание жидкости на полу на площади квадрата f, м2 расстояние от границы горения до стены с оконными и дверными проемами, через которые будет происходить газообмен при пожаре в помещении с внешней средой, l, м (см. рис. 19.3) / 2 /.
Механическая вентиляция при возникновении пожара выключается. За счет естественного газообмена в помещение поступает такое количество воздуха, что на 1 кг горящей жидкости в среднем приходится VА, м3 воздуха.
Рассчитайте возможную температуру среды в помещении при возникновении пожара:
а) среднеобъемную через 5, 15 и 30 мин его развития;
б) локальную в точке над факелом под перекрытием через 5, 15 и 30 мин его развития;
в) локальную в точках, находящихся на высоте 1,5 м от пола и расстояниях от границы горения 0,25 l, 0,5 l, 0.75 l и l, через 2 мин его развития.
Постройте графики:
а) изменения среднеобъемной температуры среды в помещении при пожаре во времени;
б) изменения температуры среды в точке над факелом под перекрытием во времени;
в) изменения температуры среды на высоте 1,5 м в зависимости от расстояния от границы горения для 2 мин развития пожара.
По графику установите, на каком расстоянии от выхода значение температуры среды достигает 700С.
Исходные данные для выполнения расчета приведены в таблице 2.1.
Таблица 2.1
| Последняя цифра шифра | ||||||||||
| a, м b, м H, м l, м | ||||||||||
| Предпоследняя цифра шифра | ||||||||||
| f, м2 VА, м3/кг | ||||||||||
| Жидкость | Ацетон | Бензин | Бензол | Диэтиловый эфир | Толуол | Этиловый спирт | Ксилол | Метиловый спирт | Амиловый спирт | Бутиловый спирт |
Задача 2.2. Нестационарная теплопроводность. Изменяющиеся граничные условия 3 рода
Рассчитайте температурное поле по толщине перекрытия через 0,5 ч после начала пожара, используя полученные при решении задачи 2.1 результаты расчета температуры среды над факелом под перекрытием (график изменения температуры среды под перекрытием). Перекрытие представляет собой сплошную железобетонную плиту толщиной 18 см. Толщина слоя бетона λ = 1,2 Вт/(м∙К). Начальная температура перекрытия 200С, такую же температуру имеет воздух над перекрытием.
Задачу решить методом конечных разностей графически.
Задача 2.3. Нестационарная теплопроводность.
Не изменяющиеся граничные условия 3 рода
Железобетонная плита перекрытия толщиной δ обогревается с одной стороны средой с температурой tг в течение τ мин. Коэффициент теплообмен а на обогреваемой поверхности плиты α = 11,63 е0,0023tг. Начальная температура перекрытия t0 = 200C. Коэффициент теплопроводности железобетона λ = 1,2 Вт/(м∙К), коэффициент температуропроводности α = 5,6∙10-7 м2/с.
Рассчитать температуру на расстоянии s от обогреваемой поверхности плиты: а) принимая перекрытие за неограниченную пластину; б) принимая перекрытие, как полуограниченное тело.
Данные, необходимые для расчетов, приведены в таблице 2.2.
Таблица 2.2
| Последняя цифра шифра | ||||||||||
| δ, м s, м | 0,25 0,02 | 0,18 0,04 | 0,20 0,03 | 0,30 0,05 | 0,25 0,08 | 0,30 0,08 | 0,25 0,06 | 0,27 0,05 | 0,20 0,09 | 0,18 0,1 |
| Предпоследняя цифра шифра | ||||||||||
| tг,0С τ, мин |
Таблица 2.3
таблица теоретических вопросов
| Последняя цифра зачётной книжки. | |||||||||||
| Предпоследняя цифра З.К. | |||||||||||
| 1; 21 | 2; 22 | 3;23 | 4; 24 | 5; 25 | 6; 26 | 7; 27 | 8; 28 | 9; 29 | 10; 30 | ||
| 11; 31 | 12; 32 | 13; 33 | 14; 34 | 15; 35 | 16; 36 | 17; 37 | 18; 38 | 19; 39 | 20;40 | ||
| 10,30 | 11,31 | 12,32 | 13,33 | 14,34 | 15,35 | 16,36 | 17,37 | 18,38 | 19,39 | ||
| 11;21 | 12; 22 | 13; 23 | 14;24 | 15; 25 | 16; 26 | 17; 27 | 18; 28 | 19; 29 | 20;30 | ||
| 1; 31 | 2; 32 | 3; 33 | 4; 34 | 5; 35 | 6; 36 | 7; 37 | 8; 38 | 9; 39 | 10,40 | ||
| 20;40 | 19;39 | 18;38 | 17;37 | 16; 36 | 15; 35 | 14; 34 | 13; 33 | 12; 32 | 11;31 | ||
| б | 10;30 | 9;29 | 8;28 | 7;27 | 6;26 | 5;25 | 4;24 | 3;23 | 2;22 | 1;21 | |
| 11; 40 | 12; 39 | 13; 38 | 14; 37 | 15; 36 | 16; 35 | 17; 34 | 18; 33 | 19; 32 | 20; 31 | ||
| 1; 30 | 2; 29 | 3; 28 | 4; 27 | 5; 26 | 6; 25 | 7; 24 | 8; 23 | 9; 22 | 10; 21; | ||
| 1;40 | 18;10 | 2;31 | 6;17 | 21;15 | 18;33 | 22;44 | 5;22 | 11;15 | 33;12 |