Контрольная работа №1
Задача 1.1. Время образования взрывоопасной концентрации
τ = М1/G1,
где М1 – масса газа в помещении при концентрации, равной нижнему концентрационному пределу воспламенения (НКПВ), кг;
G1 – расход газа через отверстие в трубопроводе, кг/с (§ 7.3, 7.4 /1/).
Из уравнения состояния (§ 1.2, 1.4/1/)
М1 = pr1V/R1T
Здесь p, V, T – соответственно, давление, объем и температура смеси (данные по условию); r1 – значение НКПВ газа в объемных долях (приложение 1); R1 = 8314/μ1 – газовая постоянная, Дж/(кг*К); μ1 = молекулярная масса газа (приложение 1).
______________________________
G1 = ξf√2kp21[(p/p)2/k – (p/p1)(k+1)/k]/(k-1)R1T1
если p/p1 > β = [2/(k+1)]k/(k-1)
______________________
G1 = ξf√kp21[2/(k+1)](k+1)/(k-1)/R1T1
если p/p1 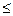 β = [2/(k+1)]k/(k-1)
β = [2/(k+1)]k/(k-1)
k – показатель адиабаты (приложение 1).
Молекулярная масса смеси (§ 1.4/1/)
μсм = rμ + r1μ1,
где μ – молекулярная масса воздуха (приложение 1);
r = 1- r1 – объемная доля воздуха в смеси
Удельная газовая постоянная смеси (§ 1.2, 1.4/1/)
Rсм = 8314/μсм.
Плотность смеси (§ 1.2, 1.4/1/)
ρсм = p/RсмT
Удельный объем смеси (§ 1.2, 1.4/1/)
νсм = RсмT/p
Изобарная теплоемкость смеси (§ 1.2, 1.4/1/)
Сpсм = Cpg – Cp1g1
где Cp и Cp1 – соответственно, массовая удельная теплоемкость воздуха и газа, Дж/(кг*К); g и g1 – соответственно, массовые доли воздуха и газа (§ 1.4/1/)
g = μr/μсм; g1 = μ1r1/ μсм
Сp = μCp/μ; Сp1 = μ1Cp1/μ1
μCp и μ1Cp1 – соответственно, мольная теплоемкость воздуха и газа, Дж/(моль*К) (приложение 1).
Порядок решения задачи
1. Установите, с дозвуковой или звуковой скоростью будет истечение газа (по величине отношения p/p1).
2. Рассчитайте секундный расход газа.
3. Выпишите значение НКПВ газа.
4. Рассчитайте удельную газовую постоянную горючего газа.
5. Рассчитайте массу газа в помещении при НКПВ.
6. Рассчитайте время образования взрывоопасной концентрации.
7. Рассчитайте среднюю молекулярную массу, газовую постоянную, плотность и удельный объем взрывоопасной смеси.
8. Выразите состав смеси в массовых долях.
9. Рассчитайте изобарную удельную массовую теплоемкость смеси.
Задача 1.2. Максимальная длина рукавной линии
l = Q/kπdср(tж – tв)
где Q – количество теплоты, отдаваемое водой воздуху в единицу времени, Вт (равно изменению энтальпии воды ∆Y § 2.4); k – коэффициент теплопередачи от воды к воздуху, Вт/(м2∙К) (§ 23.1 /1/); tж = (t'ж + t"ж)/2 – средняя температура воды, 0С; tв – температура воздуха, 0С; dср = d + δ – средний диаметр рукава, м.
∆ Ј = СжGж(t'ж - t"ж)
где Сж – теплоемкость воды, Дж/(кг∙К); Gж = πd2ωжρж/4 – массовая подача подача воды по рукаву, кг/с; ρж – плотность воды, кг/м3
k = 1/(1/α1 + δ/λ + 1/α2)
где α1 – коэффициент теплоотдачи от воды к поверхности рукава, Вт/(м2∙К); α2 – коэффициент теплоотдачи от поверхности рукава к воздуху, Вт/(м2∙К) (§ 20.2 /1/).
Значение α1 рассчитывают по одной из следующих формул: (20.10), (20.14), (20.15) /1/. Вид формулы зависит от величины комплекса ωжd/νж = Re, называемого числом Рейнольдса. Если Re>104, то коэффициент теплоотдачи находят из формулы (20.15), которую можно представить так:
α1 = 0,021λ0,57жω0,8ж(Сжρж)0,43/ν0.,37жd0,2
значение α2 также рассчитывают по одной из формул (20.20), (20.21), (20.22) /1/ в зависимости от величины комплекса ωвd/Vв. Эти формулы в явном виде можно записать, соответственно, следующим образом:
α2 = 0,5ω0,5вλ0,62в(Свρв)0,38/ν0,18жd0,5
α2 = 0.25ω0,6вλ0,62в(Свρв)0,38/ν0,22жd0,4н
α2 = 0.23ω0,8вλ0,63в(Свρв)0,37/ν0,43жd0,2н
значения параметров воды λж, Сж, ρж, νж выписать из приложения УIII /2/ при средней температуре воды. Значения параметров воздуха λв, Св, ρв, νв выписать из приложения УI /2/ при температуре воздуха. В указанных формулах для условий данной задачи сомножитель (Рrж/Prс)1/4 ≈ 1, и поэтому не учитывается.
Порядок решения задачи
1. Выпишите значения: кинематического коэффициента вязкости, коэффициентов теплопроводности, удельной изобарной теплоемкости, плотности воды и воздуха.
2. Рассчитайте число Рейнольдса при движении воды в рукаве. Установите режим движения. Подберите формулу для расчета коэффициента теплоотдачи от воды к стенке рукава.
3. Рассчитайте число Рейнольдса при поперечном обтекании рукава воздухом. Установите вид движения. Выберите формулу для расчета коэффициента теплоотдачи от поверхности рукава к воздуху.
4. Рассчитайте коэффициент теплоотдачи от воды, движущейся по рукаву, к воздуху.
5. Рассчитайте величину допустимого уменьшения энтальпии воды при движении в рукаве.
6. Рассчитайте максимальную длину рукавной линии при соблюдении условия допустимого уменьшения энтальпии воды.
Задача 1.3. Условия безопасности будут соблюдаться тогда, когда результирующая плотность теплового потока излучением между факелом и поверхностью соседнего объекта qфп будкт меньше значения допустимой qкр
qфп≤qкр
с учетом коэффициента безопасности
βqфп≤qкр
Результирующая плотность теплового потока между факелом и поверхностью тела рассчитывается по формуле
q п = εпрС0[(Тф/100)4 – (Тдоп/100)4]φ
где С0 = 5,77 – коэффициент излучения абсолютно черного тела, Вт/(м2∙К); εпр = 1/(1/εф + 1/ε – 1) – приведенная степень черноты системы факел-поверхность; φ- средний по поверхности полный коэффициент облученности факелом поверхности объекта.
Коэффициент облученности является геометрической характеристикой системой двух взаимноизлучающих поверхностей (см. § 22.3/1/). Его величина зависит от формы, размеров и взаимного расположения этих поверхностей. Формулы для расчета значения коэффициента облученности для конкретных условий приведены в табл. 22.2/1/ и приложении ХХХУ/2/.
Полагаем, что загорание облучаемой поверхности начинается с элементарной площадки dF. По условию проекция факела на вертикальную поверхность имеет форму прямоугольника конечных размеров. В таком случае взаимное расположение в пространстве факела и облучаемой поверхности является плоскопараллельным – элемента поверхности и площадки конечных размеров (см. п. 4 приложение ХХХУ/2/ или табл. 22.2/1/).
Значение φ12 рассчитывается по приведенной в /1/ или /2/ формуле. Средний по поверхности полный коэффициент облученности φ=4φ12. Расчет упрощается, если для нахождения значения φ12 использовать приведенный в литературе график φ12 =f(a/r, b/r) (см. рис. 22.8/1/ или рис. 16.2/2/). В формуле и на графике, как видно из схемы, приняты следующие обозначения: a и b – стороны прямоугольника (а=d/2, b= l /2), r(h) – расстояние между факелом и поверхностью облучаемого объекта.
Минимальное безопасное расстояние будет при соблюдении условия
Βqфп = qkp
В задаче все величины, входящие в расчетное уравнение для qфп, за исключением φ, имеют постоянное значение. Значение φ, по условию может изменяться только в том случае, если расстояние между факелом и поверхностью объекта будет меняться.
Решить задачу – это значит подобрать такое расстояние r, при котором будет соблюдаться равенство, записанное выше. Задачи такого типа решаются методом последовательных приближений, задаваясь расстоянием r. Если за три приема удовлетворительного результата не получается, то полезно построить график Βqфп = f(r) и по нему выбрать значение r, соответствующие qkp. Расчет выполнить в следующем приближении.
Подобным образом решается задача по определению величины противопожарного разрыва между объектами.
Подбор расстояния r, при котором Βqфп = qkp можно сделать по номограмме рис. 16.2/2/. Методика изложена в примере 16.6/2/.
Порядок решения задачи
1. Задайтесь расстояние r между горящим объектом и соседним с ним, считая его безопасным. Определите величину коэффициента облученности по графику или рассчитайте по формуле для этого случая.
2. Рассчитайте величину плотности теплового потока излучением, падающего на сгораемую элементарную поверхность соседнего с горящим объекта.
3. Сравните полученное расчетом значение плотности теплового потока, падающего на элементарную площадку, с допустимым (критическим) значением. При неудовлетворительном совпадении расчетного значения плотности теплового потока с критическим (расхождением более ±5%) расчет безопасного расстояния выполнить во втором (третьем и т.д.) приближении. Аналогично рассчитайте безопасное расстояние для личного состава.
Контрольная работа №2
Задача 2.1 Расчет возможного температурного режима при пожаре в помещении выполняется с целью установления:
а) действительного предела огнестойкости строительных конструкций; б) времени эвакуации людей из помещения; в) времени срабатывания датчиков пожарной автоматики и в других случаях.
Среднеобъемная температура среды в помещении при пожаре для любого заданного момента времени τ от начала его развития:
Tm,τ = 0,66 Ta(ηBcpVг/σ0εпрFT3a)0,17,
где Ta – температура продуктов горения, К
Ta = (ηQpн/cpVг) + 273
Здесь η – коэффициент полноты горения (η = 1); Qpн - теплота сгорания жидкости, Дж/кг (приложение 2); Vг – приведенный действительный объем продуктов горения, образующихся при сгорании 1 кг жидкости и коэффициенте избытка воздуха αm, м³/кг
Vг = V°г +V0(αm -1),
V°г – объем продуктов горения, образующихся при сгорании 1 кг горючей жидкости и теоретически необходимом количестве воздуха, м³/кг (приложение 2); V0 – количество воздуха, необходимого для полного сгорания 1 кг горючей жидкости, м³/кг (приложение 2); αm - коэффициент избытка воздуха, вычисляется по формуле
αm = Vд/Vо,
В – масса жидкости, сгорающей при пожаре за секунду (расход горючей жидкости) кг/с
____
В = Мо(0,3+0,7√τ/30)ƒ,
где Мо – массовая скорость выгорания жидкости, кг/(м²∙с) (приложение 2); τ – время, отсчитываемое от начала пожара, мин; Ср – удельная объемная изобарная теплоемкость продуктов горения при постоянном давлении, Дж/(м³∙К)
Ср = 1250 + [0,12 + 0,1/(0,25 + αm)]Тm,τ.
σ0 = 5,7∙10-8 - константа излучения абсолютного черного тела, Вт/(м²∙К); Епр - приведенная степень черноты системы «среда – поверхность ограждения»
Епр = 1/[1 + 0,0022(Тm,τ - 273)],
F – площадь поверхностей теплообмена, м²
F = 2(α + b)H + 2ab.
Локальное значение температуры среды в помещении при пожаре для любого момента времени τ
Тх,у, τ - Тm,τ (0,8 + 0,2У/0,5Н) [1,33 - χ/(2χ + 0,5 l)].
Над факелом под перекрытием (χ = 0, у = Н)
То,н,τ = 1,6 Тm,τ.
На высоте от пола (у = 1,5) и на любом расстоянии от границы горения
Тχ,1,5, τ = Тm,τ(0,8 + 0,6/Н) [1,33 - χ/(2χ + 0,5 l)].
Для расчета среднеобъемной температуры в помещении при пожаре необходимо знать значения приведенной степени черноты Епр и удельной теплоемкости Ср. Значения этих физических величин, как видно, являются функцией искомой температуры. Такие задачи решаются методом последовательных приближений.
Задаваясь значением искомой величины Тm,τ, определяют Епр и Ср, а затем рассчитывают среднеобъемную температуру. При неудовлетворительном совпадении результата расчета температуры с принятым ее значением операцию повторяют. Результат расчета температуры в первом приближении берут за исходную величину.
Величиной Тm,τ для нахождения значений Епр и Ср приходится задаваться, исходя из опыта и практики расчета. Полезно воспользоваться графиком рис.19.2/2/ и определить ориентировочно значение tm,τ.
Методика определения среднеобъемной температуры для любого момента времени от начала пожара по номограмме рассмотрена в примере 19.7/2/ и в § 25.2 стр.395/1/.
Порядок решения задачи
1. Выпишите из приложения 2 значения Qpн, V0г и V0 для заданной жидкости.
2. Рассчитайте среднее значение коэффициента избытка воздуха αm.
3. Рассчитайте приведенный объем продуктов горения Vг.
4. Рассчитайте средний расход горючей жидкости В (В1, В2, В3,...) соответственно за время развития пожара τ = 2 мин (5, 15 и 30 мин).
5. Задайтесь значением среднеобъемной температуры в помещении для τ = 2 мин развития пожара. (Здесь полезно воспользоваться номограммой рис. 19.7/2/).
6. Рассчитайте удельную объемную изобарную теплоемкость среды Ср в помещении при пожаре.
7. Рассчитайте значение приведенной степени черноты системы Епр.
8. Рассчитайте значение теоретической температуры горения жидкости Та.
9. Рассчитайте значение среднеобъемной температуры среды Тm,τ в помещении для τ = 2 мин развития пожара.
10. Сравните полученное расчетом (п.9) значение среднеобъемной температуры с принятым ранее значением ее для нахождения величин Ср и Епр (пп. 6 и 7). При неудовлетворительном совпадении (расхождение более ±10%) следует задаться новым значением Тm,τ и расчет выполнить в следующем приближении.
11. Рассчитайте значение температуры под перекрытием над факелом для τ = 2 мин развития пожара.
12. Рассчитайте температуру среды в помещении на заданных расстояниях от границы горения на высоте 1,5 м от пола для τ = 2 мин развития пожара. По результатам расчетов этого пункта постройте график T = f(χ).
Расчеты по пп.5-10 выполните для 5, 15 и 30 мин развития пожара в помещении. По результатам расчетов постройте графики Tm = f(τ) и Т(х = о, у = н) = f(τ). Последний график в дальнейшем используется для расчета температурного поля в плите перекрытия (задача 2.2 задания), поэтому его следует выполнить на отдельном листе в удобном для работы масштабе.
Задача 2.2. В теории теплообмена при решении задач теплопроводности известными могут быть: температура на внешней поверхности тела, плотность теплового потока на поверхности тела, температура среды, омывающей поверхность тела, и закон теплообмена между средой и поверхностью тела (коэффициент теплоотдачи).
Первый тип задач называют задачами с граничными условиями 1 рода. Второй - задачами с граничными условиями 2 рода. Третий - задачами с граничными условиями 3 рода.
Исходные данные в рассматриваемый период могут изменяться или иметь постоянные значения. В соответствии с этим граничные условия называют изменяющимися или постоянными. Во время пожара, как правило, температура среды и коэффициент теплоотдачи имеют переменные значения.
Задачи теплопроводности с изменяющимися граничными условиями 3 рода наиболее просто решаются методом конечных разностей. Суть метода изложена в § 16.3 и 16.8/1/. Графическое решение представляет собой приближенное изображение температурного поля в плите для каждого расчетного момента времени τ (τ = ίΔτ) в координатах χ, t. Данные по температуре греющей среды и условиям теплообмена на поверхности тела графически изображаются точкой (при изменяющихся во времени граничных условиях – точками) с абсциссой λ/α1 и ординатой tг с обогреваемой стороны и абсциссой λ/α2 и ординатой tо с необогреваемой стороны плиты. Оси абсцисс перпендикулярны внешним поверхностям плиты и направлены от поверхностей в сторону среды. Начало отсчета абсцисс (χ = 0) находится на внешних поверхностях плиты. Масштаб при изображении толщины стенки и граничных условий одинаков.
В примере 12.25/2/ дана методика решения задачи.
Важно правильно выбрать расчетный интервал времени Δτ и толщину расчетного слоя Δχ.
При графическом решении
Δχ = 2λ / α1max,
где α1max – максимальное значение коэффициента теплоотдачи на обогреваемой поверхности за период нагревания (τ = 30 мин), Вт/(м2 ∙ 0С)
α1max = 11,63 е0,0023 tmax,
где tmax – максимальное значение температуры среды за время пожара по результатам расчета задачи 2.1 (см.график изменения температуры среды под перекрытием), 0С.
Перекрытие условно разбивается на n слоев
n = δ/Δχ.
Если n получается не целым числом, то его следует округлить в большую сторону. После округления уточнить толщину расчетного слоя. (В случае, если n получается меньше 3, число расчетных слоев принимают равным 3)
Δχ = δ/n.
Это значение Δχ следует в дальнейшем использовать при решении задачи.
Интервал времени, через который выполняется каждый последующий расчет температуры греющей среды и температурного поля
Δτ = Δχ2/2α.
(Удобно использовать единицу времени-мин). Используя график изменения температуры под перекрытием (см.решение задачи 2.1), выписать значения температуры среды через полученный расчетом интервал времени Δτ вплоть до 30 мин (с точностью Δτ). Рассчитать значения коэффициента теплоотдачи с соответствии с температурой среды для каждого времени по формуле
α1 = 11,63 е0,0023tг
и результаты расчетов занести в таблицу
| τ, мин | tг, 0С | α1, Вт/(м2∙0С) | λ/ α1, м | α2, Вт/(м2∙0С) | λ/ α2, м |
Δτ
2 Δτ
......
l Δτ
Заполнив графы 1,2,3,4, можно приступить к решению задачи. Графическое решение целесообразно выполнять на миллиметровой бумаге. Графы 5,6 заполняются после того, как в ходе решения задачи будет установлено, что температура на внешней (необогреваемой) поверхности плиты перекрытия стала выше температуры окружающего воздуха (см. пример 12.25 /2/ п.13). Значение α2 рассчитывается по предложенным в указанной литературе формулам.
Основой для графического расчета является формула
tn,τ = (tn-1,τ + tn+1,τ)/2
где tn,τ + Δτ – температура в расчетном слое для расчетного момента времени tn-1,τ; tn+1,τ – температура в слое, предыдущем расчетному, для предыдущего момента времени τ; tn+1,τ – температура в слое, последующем за расчетным, для предыдущего расчетному момента времени τ.
Значения tn-1,τ и tn+1,τ известны из ранее выполненных расчетов или даны по условию. Из формулы видно, что слагаемые должны быть одного временного порядка.
Порядок решения задачи
1. Выпишите максимальное значение температуры среды (для 30 мин) под перекрытием над факелом при пожаре в помещении, полученное расчетом при решении задачи 2.1.
2. Рассчитайте максимальное значение коэффициента теплоотдачи на поверхности плиты со стороны пожара.
3. Установите максимальную толщину расчетного слоя Δχ.
4. Установите максимальный расчетный интервал времени Δτ.
5. По графику изменения температуры среды над факелом под перекрытием (из решения задачи 2.1) определите температуру среды через Δτ, 2Δτ, 3Δτ,...., 30 мин и запишите.
6. Рассчитайте значения коэффициента теплоотдачи α1 на поверхности плиты со стороны пожара для времени Δτ, 2Δτ,...., 30 мин.
7. Рассчитайте величину абсциссы λ /α, направляющей точки для времени Δτ, 2Δτ,...., 30 мин.
8. Начертите разрез плиты и разделите на n расчетных слоев толщиной Δχ каждый. Проведите осевые линии слева и справа за границами плиты на расстоянии Δχ/2 от ее поверхностей. Прономеруйте осевые линии слева направо N, I, II, III,..., М (оси N и M проходят вне плиты). По оси ординат выберите масштаб температуры.
9. Зафиксируйте на плоскости в координатах λ/α1 (абсцисса) t (ордината) положение направляющей точки А (А1, а2, А3,...) для каждого расчетного момента времени τ (Δτ, 2Δτ,...., 30 мин). Ордината точки соответствует температуре среды в расчетное время, а абсцисса равна отрезку λ/α1 для этого же времени.
10. Рассчитайте графически температурное поле в плите. Расчет ведется последовательно для времени Δτ, 2Δτ,.... через интервал времени Δτ.
11. На графике изобразите начальное температурное поле в плите, на каждой осевой (0, I, II,...) отложите отрезок, соответствующий в масштабе начальной температуре в плоскостях, проходящих через осевые. На вершине каждого отрезка укажите порядок расчетного интервала времени. (Для начального времени 0). По условию задачи при τ = 0 температура по всему сечению плиты равна t0. Начальное температурное поле в плите изобразится прямой (0,0,0,...), параллельной оси абсцисс.
12. Соедините отрезком (0,0) значение температуры на осевой N для времени τ = 0 со значением температуры на осевой II для этого же времени (τ = 0). Точка пересечения отрезка (0,0) с осью I отсекает ординату, соответствующую значению температуры на этой оси для времени Δτ. Точку пересечения на оси I обозначьте индексом I. Индекс будет указывать порядок расчетного интервала времени. Соедините отрезком (0,0) значение температуры на осевой I для времени τ = 0 со значением температуры на осевой III для этого же времени. Точка пересечения отрезка с осью II отсекает ординату, соответствующую значению температуры на оси II для первого расчетного интервала времени Δτ. Точку пересечения на оси II обозначьте индексом I. Индекс имеет тот же смысл, что и ранее. Аналогично определяйте температуру для времени Δτ на осях III,... Завершается расчет температурного поля для времени Δτ определением температуры на оси N. Для этого соедините точку I на оси I с направляющей точкой I; точке пересечения отрезка (I, I) с осью N присвойте индекс I.
Ломанная I-I-I... приближенно соответствует температурному полю в плите для времени Δτ. Температура на осевых I, II, III,... равна начальной.
Аналогично устанавливается температурное поле в плите для времени 2Δτ (3Δτ,..., 30 мин). Основой для решения служат результаты расчета температурного поля в плите для времени Δτ (времени предыдущего рассматриваемому моменту). На ломанной проставляйте индексы, указывающие порядок расчетного интервала времени. Верхняя ломанная должна иметь индекс одного порядка. Каждый расчет начинайте с определения температуры на осевой I и завершайте определением температуры на осевой N (слева от плиты).
Задача 2.3. Для решения задач теплопроводности с неизменяющимися граничными условиями 3 рода получено уравнение, позволяющее рассчитывать одновременное температурное поле в неограниченных плоских пластинах. При нагревании пластины с двух сторон используется формула (17.13) /1/.
При одностороннем нагревании плиты толщиной δ в течении τ мин температура на расстоянии χ от необогреваемой поверхности рассчитывается по формуле
∞
tχ,τ = tг – (tг – t0) Σ А i cos(μ i χ/δ) е-μ²iFo
l =1
где tг – температура греющей среды, 0С; t0 – начальная температура плиты, 0С. А i = 2sinμ i /(μ i + sinμ i cosμ i) – коэффициент; μ i – корень характеристического уравнения; F0 = ατ/δ2 – число Фурье; χ = δ – s – расстояние от начала координат до заданной изотермической поверхности в плите, м.
Для случая, когда F0 ≥ 0,25, можно ограничится только одним первым членом ряда. Если F0 < 0,25, то нужно взять сумму трех первых членов ряда.
Значение μ1, μ2, μ3 в зависимости от величины числа Био (Bi = αδ/λ) приведены в приложении XXX /2/ или табл. 17.1 /1/. При расчете Аi следует иметь ввиду, что значение μi в радианах.
Коэффициенты А1, А2, А3 в зависимости от величины числа Био приведены в приложении XXXI /2/.
При одностороннем нагревании на необогреваемой поверхности плиты перекрытия χ = 0, а на обогреваемой поверхности χ = δ.
При нагревании полуограниченного тела в течении τ мин температура на расстоянии χ = s от обогреваемой поверхности рассчитывается по формуле
__ __ __
tχ,τ = t0 + {1 – erf(s/2√aτ) – exp[α(s + αaτ/λ)/λ][1 - erf(s/2√aτ + α√aτ/λ)]}(tг – t0)
где erfА – функция Крампа. Значения функции в зависимости от величины аргумента А даны в приложении ХХIХ /2/ или таб. 17.3 /I/
__ __ __
А1 = s/2√aτ, А2 = s/2√aτ + α√aτ/λ.
Порядок решения задачи
а) принимая плиту как плоскую стенку
1. Рассчитайте числа Био и Фурье.
2. По числу Фурье оцените, сколько членов ряда в расчетном уравнении следует учитывать.
3. По числу Био выпишите значение μ.
4. Рассчитайте температуру в плите перекрытия на заданном расстоянии от поверхности.
б) принимая плиту за полуограниченное тело
1.Рассчитайте аргументы функции Крампа (Гауссового интеграла ошибок).
2.Определите значения функции.
3.Рассчитайте значение искомой температуры.
Примечание. Результаты расчетов а) и б) хорошо совпадают, если А1>0,6
ПРИЛОЖЕНИЯ
Приложение 1
| Наименование газов | Химическая формула | Молекулярная масса μ | Мольная μс, теплоемкость, кДж/(моль∙К) | Показатель аджабаты k | НКПВ, % (об) |
| Аммиак Ацетилен Бутан Бутилен Водород Воздух Метан Пропан Пропилен Этан Этилен | NH3 C2H2 C4H10 C4H8 H2 CH4 C3H8 C3H6 C2H6 C2H4 | 26,04 58,12 56,11 2,016 28,97 16,04 44,09 42,08 30,07 28,05 | 35,6 43,93 97,78 89,33 29,12 35,71 73,51 63,98 52,65 43,56 | 1,3 1,24 1,09 1,12 1,4 1,4 1,3 1,13 1,15 1,19 1,25 | 15,5 1,9 1,6 - 2,1 2,2 2,9 |
Приложение 2
| Наименование жидкости | М∙102, кг/(м2с) | Qpн , жДж/кг | V0, м3/кг | V0г , м3/кг |
| Амиловый спирт Ацетон Бензин Бензол Бутиловый спирт Диэтиловый эфир Ксиол Метиловый спирт Толуол Этиловый спирт | 1,75 4,33 7,17 1,36 2,89 1,61 4,72 3,06 | 9,1 7,26 11,6 10,2 8,64 8,64 10,57 4,99 10,46 6,69 | 8,14 12,6 10,68 9,52 9,55 11,8 6,06 11,94 7,76 |
М – массовая скорость выгорания (следует читать М ∙ 102 кг/(м2с) = 1,75, т.е. М = 1,75 ∙ 10-2 кг/(м2с); Qpн – низшая рабочая теплота сгорания; V0 – теоретический объем воздуха, необходимый для горения; V0г - теоретический объем продуктов горения (коэффициент избытка воздуха αm = I).
ЛИТЕРАТУРА
- Романенко П.Н., Кошмаров Ю.А., Башкирцев М.П. Термодинамика и теплопередача в пожарном деле. – М.: ВИПТШ МВД СССР, 1977.
- Задачник по термодинамике и теплопередаче в пожарном деле. Под ред. канд. тех. наук доцента М.П. Башкирцева. - М.: ВИПТШ МВД СССР, 1979.
3. Нащокин В.В. Техническая термодинамика и теплопередача. Учеб.пособие для
вузов.-М.: Высшая школа, 1980.