РАЗДЕЛ 1. КОМПЛЕКСНЫЕ ЧИСЛА
Лекция 1. Понятие комплексного числа. Алгебраическая форма
1.1. Понятие комплексного числа
В курсе высшей математики доказывается теорема о том, что любое уравнение имеет количество корней, равное степени уравнения. При этом квадратное уравнение 
не имеет решения из множества действительных чисел. Следовательно, возникает необходимость расширить понятие числа и ввести новое множество, которое позволит извлекать корни четной степени из отрицательных чисел.
Новое множество – это множество комплексных чисел. Обозначается: «С»
Определение: комплексным числом называется упорядоченная пара вещественных (действительных) чисел (a; b), где а – вещественная часть комплексного числа.
Любое вещественное число может быть представлено в виде: а = (а; 0) (но не (0; а)!!)
Два комплексных числа Z1 = (a; b) и Z2 = (c; d) считаются равными (Z1 = Z2), если a = c и b = d
1.2. Операции над комплексными числами
1) Сложение: 
1.1) Противоположное комплексное число: Z и –Z: 
2) Умножение: 
При умножении комплексного числа на действительное число: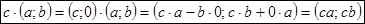 
; 
для любого к.ч.
3) Операция деления на комплексное число, отличное от нуля, возможна. В действительности, операция деления заменяется операцией умножения на обратное число.
Т.е., если 
, то обратное комплексное число 
Как всегда произведение взаимно обратных чисел равно единице: 
Все перечисленные операции удобнее выполнять над комплексными числами, записанными в алгебраической форме. Эту форму комплексного числа введем после знакомства с числом «i » - мнимой единицей.
1.3. Число «i » - мнимая единица
Рассмотрим комплексное число 
и возведем его в квадрат:
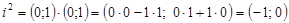, т.е. 
Это свойство числа i часто используется в дальнейшем. Например, уравнение 
, будет иметь корни: 
. Это два комплексных числа i и –i.
Можем решить и другое уравнение: 
.
Таким образом, получена возможность извлекать квадратные корни из отрицательных чисел!
При помощи числа любое комплексное число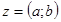 
можно записать:
1.4. Алгебраическая форма комплексного числа
Это запись комплексного числа в виде: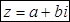 
Где a - вещественная часть, bi - мнимая часть комплексного числа.
Любое действительное число может быть представлено в таком виде:
и т.д.
Нулевое комплексное число (нуль): 
Для любых чисел: 
Лекция 2. Действия с комплексными числами в алгебраической форме
2.1. Действия
Рассматриваем числа: 
1) Сложение: 
формула (1) Свойства сложения: а) коммутативность 
б) ассоциативность: 
2) Вычитание: 
формула (2)
3) Умножение: 
формула (3) Свойства умножения: а) коммутативность; б) ассоциативность;
в) дистрибутивность: 
На самом деле, можно умножать каждое слагаемое одной скобки на каждое слагаемое другой. Так бывает проще.
Выполним рассмотренные действия для двух заданных комплексных чисел:
Пусть: 
1) 
;
2) 
;
3) 
или
Теперь, самостоятельно для чисел: 
выполните те же действия.
4) Деление: частным комплексных чисел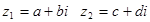 
является комплексное число 
, удовлетворяющее условию: 
или 
.
Тогда, чтобы найти число z, необходимо решить систему уравнений:
Пример: 
Операция долгая, неудобная, поэтому: введем число 
комплексно сопряженное числу 
При этом:
1) 
2) 
3) 
для любых комплексных чисел, отличных от нуля.
Тогда, удобно при делении избавляться от мнимости в знаменателе путем домножения числителя и знаменателя на число сопряженное знаменателю.
Пример: 
(тот же пример)
Фактически операция деления комплексных чисел заменяется операцией умножения на обратное число: 
Для любого комплексного числа 
- обратное число. При этом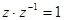 
Пример: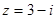 
. Найти обратное число: 
Введение обратного числа необходимо и для операции 5.
5) 
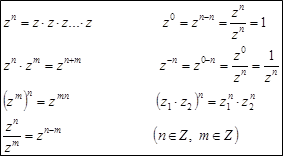Возведение в степень:
Правила
2.2. Практическая работа № 1 «Действия с комплексными числами в алгебраической форме»
1) Посчитаем степени числа :
2) Вычислить:
2.1) 
; 2.2) 
;
2.3) 
;
2.4) 
;
2.5) 
;
3) Найти решение уравнения: 
Решение: 
4) Вычислить:
4.1) 
4.2) 
4.3) 
4.4) 
4.5)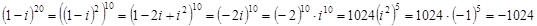 
5) Вычислить: а) число 
, если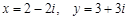 
; б) число 
Решение:
а) 
б) 