3.1. Полярные координаты
На плоскости часто применяется полярная система координат. Она определена, если задана точка O, называемая полюсом, и исходящий из полюса луч (для нас это ось Ox) – полярная ось. Положение точки M фиксируется двумя числами: радиусом (или радиус-вектором) 
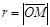и углом φ между полярной осью и вектором 
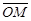. Угол φ называется полярным углом; измеряется в радианах и отсчитывается от полярной оси против часовой стрелки.
Положение точки в полярной системе координат задается упорядоченной парой чисел (r; φ). У полюса r = 0, а φ не определено. Для всех остальных точек r > 0, а φ определено с точностью до слагаемого кратного 2π. При этом парам чисел (r; φ) и (r1; φ1) сопоставляется одна и та же точка, если 
.
Для прямоугольной системы координат xOy декартовы координаты точки легко выражаются через ее полярные координаты следующим образом: 
3.2. Геометрическая интерпретация комплексного числа
Рассмотрим на плоскости декартову прямоугольную систему координат xOy.
Любому комплексному числу z=(a, b) ставится в соответствие точка плоскости с координатами (x, y), где координата x = a, т.е. действительной части комплексного числа, а координата y = bi – мнимой части.
Плоскость, точками которой являются комплексные числа – комплексная плоскость.
На рисунке комплексному числу z = (a, b) соответствует точка M(x, y).
Задание. Изобразите на координатной плоскости комплексные числа:
3.3. Тригонометрическая форма комплексного числа
Комплексное число 
на плоскости имеет координаты точки M (x; y). При этом:
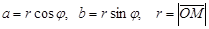
Тогда: 
.
Запись комплексного числа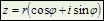 
- тригонометрическая форма комплексного числа.
Число r называется модулем комплексного числа z и обозначается 
. Модуль – неотрицательное вещественное число. Для 
.
Модуль равен нулю тогда и только тогда, когда z = 0, т.е. a = b = 0.
Число φ называется аргументом z и обозначается 
. Аргумент z определен неоднозначно, как и полярный угол в полярной системе координат, а именно с точностью до слагаемого кратного 2π.
Тогда принимаем: 
, где φ – наименьшее значение аргумента. Очевидно, что
.
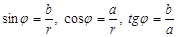При более глубоком изучении темы вводится вспомогательный аргумент φ*, такой, что 
Пример 1. Найти тригонометрическую форму комплексного числа 
.
Решение. 1) считаем модуль: 
;
2) ищем φ: 
;
3) тригонометрическая форма: 
Пример 2. Найти алгебраическую форму комплексного числа 
.
Здесь достаточно подставить значения тригонометрических функций и преобразовать выражение:
Пример 3. Найти модуль и аргумент комплексного числа 
;
1) 
;
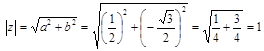2) 
; φ – в 4 четверти: 
3.4. Действия с комплексными числами в тригонометрической форме
· Сложение и вычитание удобнее выполнять с комплексными числами в алгебраической форме:
· Умножение – при помощи несложных тригонометрических преобразований можно показать, что при умножении модули чисел перемножаются, а аргументы складываются: 
;
· Деление - 
· Возведение в степень – для 
правило:
- формула Муавра (английский математик, француз по происхождению);
· Извлечение корня n- й степени.
Определение. Корнем n-й степени из числа z называется комплексное число u, для которого 
, тогда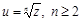 
.
Теорема. Для любого комплексного числаz, отличного от нуля извлечение корня n- й степени всегда возможно и имеет n различных решений.
Пусть 
, искомый корень 
, тогда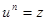 
, т.е. 
Заключение
Помимо рассмотренных операций возможно дифференцирование комплексных чисел, составление комплексных матриц и другое.
Помимо рассмотренных комплексных чисел в алгебраической и тригонометрической форме существуют комплексные числа в показательной форме, которые применяются в электротехнике при расчете электрических цепей.