Задание 1
Используя метод наименьших квадратов найти оценки коэффициентов регрессионной зависимости  . Исходные данные для расчетов приведены в таблице Б.4.1.
. Исходные данные для расчетов приведены в таблице Б.4.1.
Таблица Б.4.1

| 
|
| 1,00 | 1,43 |
| 2,00 | 5,51 |
| 3,00 | 9,23 |
| 4,00 | 13,62 |
| 5,00 | 17,49 |
Данные для каждого варианта рассчитываются следующим образом:

Задание 2
Используя метод наименьших квадратов найти оценки коэффициентов регрессионной зависимости 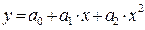 . Исходные данные для расчетов приведены в таблице Б.4.2.
. Исходные данные для расчетов приведены в таблице Б.4.2.
Таблица Б.4.2

| 
|
| 1,00 | 10,68 |
| 1,50 | 15,26 |
| 2,00 | 20,37 |
| 2,50 | 27,18 |
| 3,00 | 35,29 |
| 3,50 | 44,53 |
| 4,00 | 55,53 |
| 4,50 | 67,10 |
| 5,00 | 80,58 |
Данные для каждого варианта рассчитываются следующим образом:

Задание 3
Используя метод наименьших квадратов найти оценки коэффициентов регрессионной зависимости  . Исходные данные для расчетов приведены в таблице Б.4.3.
. Исходные данные для расчетов приведены в таблице Б.4.3.
Таблица Б.4.3

| 
|
| 1,00 | 9,16 |
| 1,25 | 8,24 |
| 1,50 | 6,88 |
| 1,75 | 5,90 |
| 2,00 | 5,88 |
| 2,25 | 5,55 |
Данные для каждого варианта рассчитываются следующим образом:
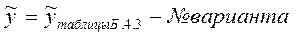
Задание 4
Найти оценки коэффициентов регрессионной зависимости  , и проверить регрессионную зависимость на адекватность для двухфакторного полнофакторного эксперимента. Исходные данные для расчетов приведены в таблице Б.4.4.
, и проверить регрессионную зависимость на адекватность для двухфакторного полнофакторного эксперимента. Исходные данные для расчетов приведены в таблице Б.4.4.
Таблица Б.4.4.

| 
| 
| 
| 
|
| -1 | -1 | 2,12 | 2,16 | 2,03 |
| -1 | 8,16 | 8,04 | 8,19 | |
| -1 | -1,99 | -1,99 | -1,84 | |
| 12,08 | 12,09 | 12,02 |
Данные для каждого варианта рассчитываются следующим образом:

Задание 5
Найти оценки коэффициентов регрессионной зависимости 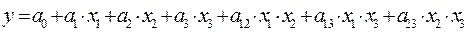 и проверить регрессионную зависимость на адекватность для трехфакторного полнофакторного эксперимента. Исходные данные для расчетов приведены в таблице Б.4.5.
и проверить регрессионную зависимость на адекватность для трехфакторного полнофакторного эксперимента. Исходные данные для расчетов приведены в таблице Б.4.5.
Таблица Б.4.5

| 
| 
| 
| 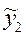
| 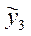
|
| -1 | -1 | -1 | 10,92 | 10,93 | 10,91 |
| -1 | -1 | -9,36 | -9,39 | -9,39 | |
| -1 | -1 | -3,06 | -3,01 | -2,95 | |
| -1 | -3,35 | -3,42 | -3,32 | ||
| -1 | -1 | 1,05 | 0,92 | 1,03 | |
| -1 | 8,64 | 8,50 | 8,59 | ||
| -1 | -5,02 | -5,04 | -4,90 | ||
| 22,66 | 22,64 | 22,58 |
Данные для каждого варианта рассчитываются следующим образом:

Задание 6
Упростить регрессионную зависимость, найти оценки коэффициентов регрессионной зависимости  и проверить регрессионную зависимость на адекватность для четырехфакторного дробнофакторного эксперимента с генерирующим соотношением
и проверить регрессионную зависимость на адекватность для четырехфакторного дробнофакторного эксперимента с генерирующим соотношением 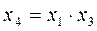 . Исходные данные для расчетов приведены в таблице Б.4.6.
. Исходные данные для расчетов приведены в таблице Б.4.6.
Таблица Б.4.6
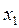
| 
| 
| 
| 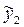
| 
|
| -1 | -1 | -1 | 8,55 | 8,46 | 8,47 |
| -1 | -1 | -5,51 | -5,41 | -5,58 | |
| -1 | -1 | -9,47 | -9,53 | -9,58 | |
| -1 | -3,56 | -3,58 | -3,51 | ||
| -1 | -1 | 2,59 | 2,51 | 2,50 | |
| -1 | 8,59 | 8,44 | 8,48 | ||
| -1 | 0,48 | 0,46 | 0,50 | ||
| 26,43 | 26,50 | 26,59 |
Данные для каждого варианта рассчитываются следующим образом:
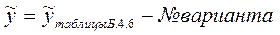
Задание 7
Определить влияние качественного фактора при однофакторном дисперсионном анализе. Исходные данные для расчетов приведены в таблице Б.4.7.
Таблица Б.4.7
| m N | |||||
| -16 | |||||
| -8 | -4 |
Данные для каждого варианта рассчитываются следующим образом:

Задание 8
Определить влияние качественных факторов при двухфакторном дисперсионном анализе с иерархической структурой. Данные для расчетов приведены в таблице Б.4.8.
Таблица Б.4.8


| |||||
Данные для каждого варианта рассчитываются следующим образом:

Задание 9
Определить влияние качественных факторов и их взаимодействия при двухфакторном дисперсионном анализе с перекрестной структурой. Данные для расчетов приведены в таблице Б.4.9.
Таблица Б.4.9


| |||||
Данные для каждого варианта рассчитываются следующим образом:
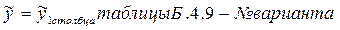
Задание 10
Построить греко-латинский квадрат размерностью 7*7 и определить влияние качественных факторов и их взаимодействия. Данные для расчетов приведены в таблице Б.4.10.
 Таблица Б.4.10
Таблица Б.4.10


| |||||||
Данные для каждого варианта рассчитываются следующим образом:

Задание 11
Определить согласованность мнений экспертов и установить, какие из факторов необходимо включать в круг рассматриваемых, влияющих на выходную величину исследуемого объекта, используя один из методов отсеивающего эксперимента (метод ранжирования априорной информации).
Данные для расчетов приведены в таблице Б.4.11.
Таблица Б.4.11
| Эксперты | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | Х9 | Х10 |
Данные для каждого варианта рассчитываются следующим образом:
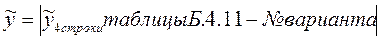
Приложение В
(обязательное)