Введение
Метод потенциалов в задаче выбора пути для мобильного робота (МР) был предложен А.К. Платоновым в 1970 году.
При этом рассматривается случай, когда робот снабжен достаточно точной навигационной системой, чтобы ее ошибками можно было пренебречь, и системе управления известны как координаты робота и измерительного устройства, так и ориентация сектора обзора и направление производящихся измерений в некоторой абсолютной системе координат (АСК). Робот во всех случаях представляет собой точку с предписанным вектором ориентации.
Суть метода заключается в следующем. Предположим, что цель имеет некоторый положительный заряд, препятствия заряжены отрицательно; местоположения цели и препятствий фиксированы. Пусть также имеется некоторая отрицательно заряженная точка, способная перемещаться. Поместим ее в исходную точку. Под действием сил подвижная точка будет притягиваться к цели и отталкиваться от препятствий, причем законы движения могут задаваться, в принципе, различными способами. Логично предположить, что при некоторых ограничениях на структуру местности и законы движения подвижной точки эта точка достигнет цели.
В зависимости от способа задания функций, можно получить трассы с обходом препятствий с той или иной степенью «риска» (величины приближения к препятствиям). Рассматриваемые ниже алгоритмы гарантируют от зацикливания в случае, когда контуры препятствий выпуклы. Метод может также использоваться для случая, когда препятствия разбиваются на группы, выпуклые оболочки которых не пересекаются.
За рубежом основные ссылки делаются на работы Брукса и Хатиба, которые вышли в свет в 1985 году [6,7]. Следует отметить, что в Японии подобные разработки были выполнены сотрудниками фирмы Hitachi, Ltd. в 1984 году [9]. Подобные же алгоритмы использовались и при трассировке печатных плат в 1967 году (см. [8], в которой дана ссылка на более раннюю работу 1948 года). Для того, чтобы проследить эволюцию архетипа основной идеи метода, ниже приводится историческая справка о разработках, имеющих отношение к методу потенциалов в задачи выбора пути.
В данной работе исследованы модификации алгоритма, изложенного в [1]. При этом рассмотрены следующие направления модификации исходного алгоритма:
1) Исследованы степенная и показательная функции отталкивания от препятствий и влияние их на результирующий путь мобильного робота (МР). Для оценки эффективности пути использовалась функция отклонения вектора направления движения от вектора направления на цель.
2) Проанализированы возможности использования метода потенциалов для управления распределенной мобильной системой (РМС). Исследовано пять способов организации такого движения:
a) Движение по схеме «цепь». В этом случае сила притяжения цели действует на «лидера», и каждый МР «притягивается» к впереди идущему.
b) Движение типа «гонка за лидером». В этом случае все элементы РМС «притягиваются» к «лидеру», который, в свою очередь, «притягивается» к целевой точке.
c) Движение типа «расхождения». В этом случае на МР, расположенные компактной группой или цепью, начинает действовать сила отталкивания от «лидера». МР «разбегаются», исследуя каждый свой участок.
d) Движение типа «схождение». В этом случае «лидер» собирает все элементы РМС в компактную группу.
e) Организация движения типа «свободный поиск». В этом случае сила притяжения к цели отсутствует, и каждый элемент РМС движется в свободном от препятствий направлении.
Первые два режима используются для организации передвижения РМС, последние три – для информационного исследования среды.
Основное отличие нового алгоритма от изложенного в [1] состоит в том, что в [1] непосредственно вычислялось расстояние до каждого из препятствий ri непосредственно, а в новом алгоритме используется имитатор дальномерной системы. Полученный массив дальностей в некотором секторе в дальнейшем подвергается логической фильтрации для построения оценок величин ri.
Историческая справка
Наряду с указанным названием – метод потенциалов (Potential Field Approach), он имеет следующие названия: способа "искусственных потенциальных полей" (artificial potential fields), "полей виртуальных сил"(virtual force field-VFF), "гистограммы векторных сил" (vector field histogram-VFH) и др. Суть этого метода, напомним, заключается в том, что путь строится на основе решения специального "уравнения движения", в которое входят "сила притяжения к цели", "силы отталкивания от препятствий " и, возможно, некоторые другие "силы". При ссылке на этот метод в качестве пионерских упоминаются работы 1985 -1986 гг. [6,7]. Вместе с тем работа фирмы Хитачи по управлению МР, в которой использованы идеи "силового поля", выпущена в 1984 г. [9]. В [1] опубликовали результаты подобного исследования в ИПМ АН СССР в 1974г. Вместе с тем использование подобных физических аналогий при трассировке электронных плат уходит корнями вглубь 50-х годов [8]. Правда, вычислительные аспекты при этом имеют свою специфику.
Сам архетип идеи движения в поле "информационных" (виртуальных) сил восходит к работам 30-х-40-х годов одного из виднейших представителей гештальтпсихологии Курта Левина. Он выступил с идеей применения в психологии концепции физического поля для описания поведения и конфликтных ситуаций при взаимодействии индивида с окружающим миром [3]. Современные психологи критикуют К. Левина за физикализм концепции, акцент на динамический аспект в ущерб содержательному и многое другое. Вместе с тем в указанных работах К. Левина можно почерпнуть немало интересного. Экспериментальный материал, подтверждающий разработанную концепцию, был получен в основном при наблюдении за детьми разного возраста и документирован посредством киносъемок. Имеет смысл привести четыре особенности поведения сил «психологического поля», выделенного К. Левиным [3]:
(1). "...сила поля исчезает (или по крайней мере сильно ослабевает) как только объект попадает в сферу "владений индивида".
(2). "... в некоторых случаях величина валентности [заряда] увеличивается с ее явной близостью. Это выражается как в продолжительности,
так и в интенсивности попыток к достижению цели".
(3). "... величина сил поля, которые соответствуют отрицательной валентности, уменьшаются намного быстрее с увеличением физического расстояния, чем это происходит с силами поля, соответствующими положительной валентности".
(4). Возможны колебания локомоций вблизи точек равновесия сил, которые называются также "годологическим конфликтом".
Все они имеют аналоги при использовании метода потенциалов для управления МР.
На начальном этапе исследований в ИПМ рассматривались препятствия в виде окружностей. Подобное представление после результатов работ Koditschek с соавторами [4,5] можно считать основным. Сила притяжения к цели полагалась постоянной по модулю и направленной к точке цели. Сила отталкивания от i -ого препятствия f i зависела от аргумента R i /r i, где R i -радиус i -ой окружности, r i -расстояние от центра i -ой окружности до движущейся точки. f i считалась направленной от центра окружности. Траектория ("локомоция") получалась в результате интегрирования уравнений движения второго порядка, так как ускорение, действующее на движущуюся точку, определялось суммой указанных сил. В ходе исследований выяснилось, что инерционность, заложенная в указанную модель, приводит к тому, что траектория движения становится малоприемлемой (препятствие "отбрасывает" движущуюся точку очень сильно и траектория получается чересчур "изрезанной". Для того, чтобы избавиться от этого недостатка и сделать метод годным для случая аппроксимации контуров препятствий другими способами, было предпринято следующее. Во-первых, стали использоваться уравнения движения первого порядка (т.е. действующие силы определяют скорость, по сути дела речь идет об аналоге простого градиентного спуска). Во-вторых, сила отталкивания стала определяться аргументом, равным расстоянию до препятствия. При этом форма контура препятствия произвольна, а для приведенного выше примера это разность r i – R i. Направлена эта сила в сторону от ближайшей точки препятствия. В ходе исследований было признано рациональным в случае наличия нескольких препятствий использовать функции от указанного аргумента x типа x -k или e -cx, которые быстро убывают с расстоянием. При этом коэффициенты k и c могут быть варьируемыми параметрами.
Следует особо подчеркнуть, что, варьируя параметры k и c при определении сил отталкивания, можно получать траектории для движения нескольких МР. Если ввести в этом процессе запаздывание, то можно получить режим "следования друг за другом".
Иногда среда, в которой расположено много препятствий, "хорошо организована", например, препятствия разбиваются на группы, выпуклые оболочки которых не пресекаются. В этом случае сила отталкивания может вычисляться сразу для всей группы.
Таким образом, метод потенциалов позволяет строить "размытые" модели среды и получать решение без учета ненужных подробностей.
Анализируя разнообразие зарубежных работ по методу потенциалов, можно выделить два интересных направления.
Первое является попыткой ответить на вопрос: можно ли эффективно задавать силовое поле так, чтобы отсутствовали устойчивые точки равновесия в принципе. Достаточно очевидно, что в общем случае ответ на этот вопрос положительный. Действительно, функция потенциала в точке x, равная минимальной длине допустимого пути от x к g - точке цели, задает такое поле. Однако эту функцию в общем случае считать весьма непросто. Koditschek с соавторами в серии работ [4,5] и др. предложили свой подход к этой проблеме, который хотя и отличается оригинальностью, в итоге оказывается вряд ли намного проще способа, указанного выше. Вначале рассматривается "Сферический мир". Для плоскости это окружности-препятствия, окруженные окружностью-рамкой. В этом мире результирующая сила определяется не как сумма сил, действующих от различных препятствий, а как произведение таких сил. Эти два положения позволяют избежать наличия точек равновесия силового поля, что зафиксировано теоретически.
Далее строится последовательность диффеоморфизмов. Поначалу между "сферическим миром" и "звездным миром" - в котором препятствия представляют многоугольники особого вида. Затем происходит переход от "звездного мира" ко все более и более " общим мирам". При этом диффеоморфизм сохраняет "безособость" получающихся при поэтапных переходах от "сферического мира" силовых полей. Однако необходимо отметить, что демонстрируемые иллюстрации подобных полей для более общих постановок, чем "сферический мир", позволяют утверждать, что для них весьма характерны "овражные эффекты". Следовательно, при фиксированном значении шага возможны в лучшем случае эффекты типа "информационного дребезга", а также зацикливание в ложном экстремуме. Возможно, что именно поэтому авторы не демонстрируют построение траекторий движения, а только картинки линий уровня.
Второе направление, берущее начало от работ исследователей Оксфордского университета, заключается в следующем. Сам МР представляется не точкой, а отрезком или прямоугольником. Это позволяет рассчитывать не только результирующую силу, действующую на МР, но и момент сил, т.е. управлять ориентацией.
Ниже приводятся некоторые ранее не публиковавшиеся результаты исследования алгоритмов, основанных на методе потенциалов, полученные в ИПМ в 70-80х гг. прошлого века.
Зависимость траектории от показателя k и шага s для функции сипы отталкивания F вида (R/r) k для случая окружности приведено на рис. 1:
(a): k=16, s=0.05, 0.1, 0.15, 0.2, 0.25
(b): k=4, 8, 12, 16, s=0.05
(c): F вида exp[- (l — A * r/R) 2 ], А=1.5
(d): F та же, что и для (a), k=12, s=0.05, 0.1, 0.2, 0.3.
Критическое отношение шага к радиусу обходимой окружности для появления информационного дребезга 0.1 для степенной функции и 0.3 для экспоненты.
Подобным образом исследовалось влияние информационного дребезга для плавного контура (окружность радиуса 1) при обходе методом потенциалов.
Рис. 2. иллюстрирует пример среды, в которой можно выделить группы препятствий. Результирующий путь получен при использовании обобщенных потенциалов.
Современное состояние
В статье [9] описывается мобильный робот (МР), разработанный фирмой Hitachi, Ltd. (Япония) в 1984 г., в котором, в частности, для реализации управления автономным перемещением, был использован так называемый «метод потенциального наведения ». Он предусматривает оснащение робота дальномерами, измеряющими расстояние до объектов в рабочей зоне. Принцип этого метода схематически представлен на рис. 3, где обозначено: Xk - точка нахождения робота в текущий момент времени; t k - направление передвижения робота до текущего момента времени; t k +1 - направление передвижения робота в текущий момент времени; XG - целевая точка; g - вектор, направленный к целевой точке; r max - максимальный радиус; r i * - вектор, проведенный до объекта, находящегося в рабочей зоне робота.
Расчет направления передвижения робота непрерывно осуществляется на основании результата сложения трех векторов с учетом соответствующих весовых функций: вектора, характеризующего направление, при котором в наилучшей степени просматривается целевая точка; вектора, характеризующего направление передвижения без столкновений с препятствиями, и вектора, соответствующего направлению движения робота до настоящего времени. При этом система управления роботом обеспечивает рациональный обход неизвестных препятствий. Управление осуществляется с использованием карты по алгоритму построения в квазиреальном времени квазиоптимальной (по расстоянию) траектории. Применение ультразвукового дальномера, установленного на роботе, обеспечивает обнаружение препятствий, причем процедура планирования траектории вновь повторяется для внесения необходимых коррекций.
В работе [10] рассматривается архитектура систем навигации реального времени, используемых в том числе для обхода препятствий мобильными роботами (МР). Подробно рассмотрены следующие результаты:
- виды архитектуры и технологии соответствующих датчиков (сенсоров);
- представление различных моделей поведения с помощью сенсорно-управляемых алгоритмов;
- метод искусственного потенциального поля – алгоритм реального времени, разработанный специально для навигации МР во процессе движения.
В рассматриваемой системе данные инфракрасных датчиков создают образ среды в некоторой окрестности МР, в соответствии с которым затем строится траектория движения. Отсюда возникают строгие ограничения на скорость движения МР, связанные со скоростью получения и обработки данных, скоростью работы навигационного алгоритма и временем реакции управляющей системы МР на изменение обстановки.
В данной реализации метода потенциалов МР представляется как точкка начала отсчета в полярных координатах, из которой вращающимся сенсором осуществляется непрерывное циклическое сканирование местности с сектором обзора 360° (рис. 4).
Пусть угол g – угловой шаг сканирования, d i - результат i –го (относительно текущего направления движения МР) замера дальности от МР до препятствия. В соответствие каждому d i ставится вектор силы fi, вычисляемый с помощью уравнений для искусственного потенциального поля:

где A – фиксированная константа. После обзора всего сектора (360°) определяются новые компоненты вектора скорости V x и V y:

где b, с физической точки зрения, есть весовой множитель, используемый для того, чтобы на компоненты скорости большее влияние оказывали силы, действующие с фронта МР, нежели сзади. Утверждается, что в общем случае b есть функция g и di:

при этом b пересчитывается каждый раз при нахождении нового вектора скорости.
Авторами статьи [11] предложен алгоритм планирования движения выпуклого многоугольного объекта в среде, содержащей многоугольные препятствия. Представлена эвристика, базирующаяся на рассмотрении моментов, что позволяет расширить алгоритм и ввести в рассмотрение дополнительную степень свободы мобильного робота (МР) – угол поворота. Также представлены результаты построения трассы для МР, движущегося по коридору.
В работе используется следующая терминология. Пусть рабочая область пространства W, в которой действует МР, является подмножеством Ân. Пусть O Ì W представляет собой множество препятствий в рабочей области, тогда свободным пространством в W будет являться множество F = W \ O; задача построения пути МР в таком случае есть задача нахождения набора точек в F, определяющих траекторию движения МР из начальной точки в точку целевую.
Сначала рассматривается простой алгоритм, в котором многоугольный объект M, имеющий две степени свободы, перемещается в рабочем пространстве W, в котором присутствует конечное множество препятствий O. Текущее положение объекта M задается вектором x, начальное положение – вектором x s, а целевая точка – вектором x g. Тогда трасса строится по следующему алгоритму:
x xs
Repeat
D min min (D(M,o)) " o Î O
F repulse D min × 1 / |D|2
F attract xg – x
F res F attract + a × F repulse
x x + F res
until (x = xg ) or (|F res | = 0)
Здесь D - вектор, доставляющий минимальное расстояние между M и препятствием o Î O. Константа a управляет влиянием препятствия на M в зависимости от расстояния. При использовании подобной потенциальной функции столкновений с препятствиями не происходит, однако, алгоритм может зацикливаться в случае достижения МР локального минимума в потенциальном поле. Для борьбы с этим явлением могут применяться различный методы, например, «барьер» из точек высокого потенциала вокруг точки локального минимума или метод Монте-Карло.
Далее для объекта M вводится дополнительная степень свободы - угол поворота q, начальная конфигурация объекта в данном случае –
(x s, q s). Предполагается, что движется в коридоре минимального потенциала (КМП). Если он ориентирован так, что момент вращения МР в потенциальном поле минимален, то движение происходит таким образом, что главная ось направлена по касательной к КМП.
Пусть c – центр масс M, а P – множество векторов, описывающих положение некоторых контрольных точек, нормально распределенных по границе M относительно c. Предыдущий алгоритм модифицируется следующим образом:
x xs
q qs
Repeat
F repulse (0, 0)
moment 0
for each p Î P
D min min (D(c + p, o)) " o Î O
F repulse F repulse + D min × 1 / |D|2
momentmoment + (p ´ D min) × k
Endfor
F attract xg – x
F res F attract + a × F repulse
x x + F res
qq + b ´ moment
until (x = xg ) or (|F res | = 0)
Константа b управляет величиной поворота и определяется эмпирически, поскольку математическое решение нетривиально и зависит от многих факторов. Кроме того, при практической реализации алгоритма, выбор c может быть неоднозначен. В рассматриваемых примерах для трехколесного МР в качестве c бралась середина оси между двумя задними колесами.
В работе [12] представлен метод обхода препятствий мобильным роботом (МР), получивший название метода «гистограмм векторных полей» (VHF-метод). Он позволяет обнаруживать препятствия и обходить их во время движения. МР, управляемый данным алгоритмом, маневрирует быстро и без остановок даже среди большого количества неупорядоченных препятствий.
VHF-метод для представления препятствий использует сетку на двумерной декартовой плоскости. Каждой ячейке сетки ставится в соответствие характерное значение, представляющее уровень «уверенности» алгоритма в присутствии препятствия в данной ячейке. Метод использует двухуровневую систему представления данных:
· на первом уровне – детальное описание среды, окружающей робота, с помощью декартовой сетки C;
· на втором уровне – полярная гистограмма H, которая строится по данным, содержащимся в C, вокруг центра масс МР как набор значений из C, соответствующий некоторым фиксированным секторам шириной a каждый. Каждому сектору k ставится в соответствие величина h k, называемая полярной плотностью препятствий в направлении k.
Выходными данными алгоритма являются сигналы управления МР.
Пусть C *, называемая активной областью, есть область сетки C размером w s ´ w s, построенная вокруг МР; ее элементами являются активные ячейки c ij. Тогда C преобразуется в H следующим образом: строятся векторы препятствий, направление которых относительно точки текущего положения МР определяется как

а модуль вектора

где a, b = const > 0;
d ij – расстояние между активной ячейкой и МР;
c * ij – среднее значение в активной ячейке (i,j);
x 0, y 0 – текущие координаты МР;
x i, y i – координаты активной ячейки (i,j).
Каждому из k секторов ставится в соответствие угол из ряда 0, a, 2 a,…, 360°- a. Тогда между k и c * ij существует следующее отношение:

Для каждого сектора k h k вычисляется

Таким образом, каждая из активных ячеек находится в одном из секторов. Однако, из-за дискретности сетки, в результате такого распределения ячеек могут возникать «ступеньки» в секторах, что может привести к ошибкам в выборе направления. Для того чтобы избежать искажения результата, используется сглаживающая функция

Далее вычисляется направление движения в полярных координатах, q free, и соответствующий ему сектор k free в H. Алгоритм выбирает более «проходимое» направление и, вместе с тем, как можно более приближенное к текущему направлению на цель q targ.
Скорость движения МР в начальной точке устанавливается максимальной (S max), а затем определяется на каждом шаге в соответствии с формулой

где
h`` c = min(h` c, h m);
h` c – сглаженная полярная плотность препятствий в выбранном направлении движения;
h m – эмпирически установленная константа.
При этом отношение (*) гарантирует S` ³ 0 при h`` c £ h m.
Статья [13] посвящена методу построения гладких трасс движения мобильного робота (МР), основанному на физической аналогии. Основными достоинствами метода являются устойчивое решение и работа не только с двоичными (препятствие или свободное пространство), но и с разнородными средами, поверхность которых может иметь неравные коэффициенты трения или углы наклона на различных участках.
В основе метода лежат физические принципы гидродинамики. Если предположить, что вся среда заполнена жидкостью, то потоки жидкости позволяют добраться из начальной точки в целевую. В этом случае оптимальным путем будет поток, направленный вдоль градиента давления, в котором достигается стационарное движение жидкости; локальный минимум не может быть достигнут, поскольку во всех точках потока удовлетворяется уравнение Лапласа. Для учета неоднородностей среды вводится внешняя сила, учитывающая силу трения и влияние проходимых препятствий, поэтому рассматриваются потоки вязкой жидкости. Основным уравнением движения вязкой несжимаемой жидкости является уравнение Навье-Стокса:
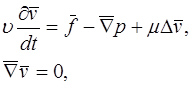
где
r - плотность жидкости;
v – вектор скорости движения жидкости;
t – время;
f – внешняя сила;
p – давление;
m - коэффициент вязкости жидкости.
Упрощенное уравнение выглядит следующим образом:

Здесь неизвестными являются вектор скорости v и абсолютная координата x.
Граничные условия:

где ¶ W - границы препятствий, n – внешняя нормаль к границе препятствия.
Начальные условия:

где x S – начальная точка, x G – целевая точка.
Для решения уравнения в двумерном пространстве методом конечных разностей уравнение представляется следующим образом: 
где

Если число точек сетки N, то необходимо решить разреженную систему из 3 N линейных уравнений.
Результатом работы рассматриваемого алгоритма является множество так называемых «коридоров». Каждый коридор начинается в окрестности стартовой точки и заканчивается в окрестности целевой. Следование МР по осевой линии коридора гарантирует его безопасность.
Далее рассматривается случай, когда внешняя сила не равна нулю, что позволяет учитывать разнородность среды.
Полная потенциальная энергия частицы в потоке:

где S – начальная точка, G – целевая точка, T – вектор, касательный к траектории, pG – pS - разность давлений в x S и x G.
В случае присутствия силы трения F
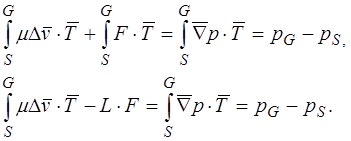
Механическая работа силы трения L×F завиcит от длины траектории L. В случае достаточно большой величины F

все траектории имеют ограниченную длину

Практически, установка очень большой величины F на границах препятствий эквивалентна условию v = 0. При использовании F = const длина потоков может быть ограничена, поэтому, увеличивая величину F, можно добиться отсеивания путей большей длины, оставляя лишь пути, длины которых близки к оптимальным.
Для тестов данного метода использовался 4-х колесный МР на полигоне 60м ´ 100м с препятствиями [13]. Внешняя сила f задавалась в виде

где m – масса МР, q - угол наклона участка поверхности в направлении движения, K f – коэффициент трения между колесами и поверхностью.
Следует отметить также направление, связанное с достаточно сложным по своей структуре заданием потенциальной функции, которая не имеет локальных минимумов [4, 5]. Однако при этом задание подобной потенциальной функции может оказаться очень сложным. Приведем простой пример, подтверждающий эту точку зрения.
Описание метода и его реализаций
Две основные характеристики метода потенциалов составляют:
1) Законы движения подвижной точки.
2) Способы задания функции отталкивания от препятствий.
Согласно теоретической механике, в данном случае уравнения движения задаются в виде (будем считать, что препятствия представляют собой окружности радиуса r i):
|
где fi – сила отталкивания от i –ой окружности, f 0 - сила притяжения к цели, r - вектор, направленный в точку цели. Однако, как показано в [1], такой способ задания уравнения движения является нецелесообразным, поскольку траектория после «соударения» с препятствием будет сильно отбрасываться назад, т.к. инерция в этом случае гасится не сразу. Поэтому путь робота строится на основе решения специального уравнения движения, которое в простейшем случае имеет вид:

 |
где x – координаты робота, f0 – сила притяжения к целевой точке, fi - сила отталкивания от i -го препятствия. В общем случае уравнение движения для построения трассы запишется в виде:
где x0 – координаты цели, l - коэффициент зон влияния, pi - параметры i –го препятствия, A - матрица поворота системы. В простейшем случае построение трассы представляет собой реализацию метода градиентного спуска с постоянным шагом.
Пусть цель притягивает подвижную точку все время с единичной силой. Тогда силу отталкивания от каждого препятствия желательно задать так, чтобы на границе она принимала единичное значение и была направлена по возможности по нормали к препятствию, а вне препятствия убывала пропорционально расстоянию. Были исследованы следующие виды функций отталкивания:
|
k, c являлись варьируемыми параметрами. Изменяя их, можно получить качественно различные виды траекторий. Так, взяв большое значение параметра k, получим траекторию, сходную с обходом препятствия по контуру – точка будет отклоняться от препятствия лишь на небольшое расстояние. С другой стороны, при малых значениях параметра k, точка будет отклоняться от препятствия раньше, однако, сферы действия различных препятствий в этом случае могут перекрываться (если препятствия расположены близко друг от друга) и возможность прохода между ними может быть пропущена.
В текущей версии алгоритма сила отталкивания от препятствий формируется на основе данных, полученных от дальномера. Фильтрация полученных дальностей до препятствия организована так, что все дальности расположенные между «скачками» (пороговое значение «скачка» задается и «скачок» фиксируется, если разность между соседними дальностями в секторе обзора превышает этот порог) считаются принадлежащими контуру одного препятствия. Далее вычисляется расстояние до видимого участка контура по минимальной дальности. Полученное минимальное расстояние до участка контура является аргументом функции отталкивания.
В ходе работы выяснилось, что при построении пути имеет смысл ввести в алгоритм вычисления правых частей уравнений движения некоторые простые эвристические правила, которые могут способствовать, например, выходу из устойчивой точки равновесия поля сил. Имеет смысл учитывать следующие обстоятельства:
a. В случае, если точка находится в достаточной близости от одного из препятствий, действием остальных можно пренебречь.
b. Угол поворота j МР на каждом шаге не должен превышать заданной величины.
c. Учитываются только те препятствия, которые попадают в сектор обзора ±(90+ j)° относительно направления на цель.
d. При попадании в достаточно близкую окрестность препятствия робот производит разворот, стоя на месте.
e. При вычислении функции отталкивания от препятствия полученное значение удобно умножать на некоторый коэффициент, зависящий от взаимного расположения в текущий момент движущейся точки, цели и данного препятствия.
Такой подход может быть реализован при введении так называемых зон влияния препятствия – областей в секторе обзора, каждая из которых имеет свой коэффициент. Использовались две зоны влияния:
1) Сектор ±45° относительно направления на цель – коэффициент 1.
2) Оставшиеся области – коэффициент 0,25.
Можно выделять и четыре зоны влияния так, как это показано на рис. 5.
Модификация алгоритма, когда поворот вектора направления движения происходит одновременно с движением точки был рассмотрен ранее в [1]. Ограничение на угол поворота робота, реализовывалось следующим образом: если вычисленная величина этого угла больше j, то вектор смещения на текущем шаге определяется как единичный вектор, отклоненный от вектора предыдущего смещения на максимально возможный угол в сторону, соответствующую отклонению результирующей силы Fрез.
При исследовании оказалось удобным рассматривать следующие характеристики построенной трассы:
1) Угол g между векторами текущего направления на цель и текущего перемещения. Если g принимает значения, близкие к нулю, то это означает, что МР движется в направлении к цели. Большие значения угла означают, что робот слабо перемещается в направлении к цели.
2) Параметр l:
l = r s / r 0,
где r s – длина построенной трассы, r 0 – расстояние от точки цели до исходной точки. Чем меньше l, тем более короткую трассу удается построить.
На рис. 6, 7 приведены примеры реализации численного моделирования алгоритма выбора пути на основе метода потенциалов в случае задания функции отталкивания от препятствия как в виде показательной функции (рис. 6а), так и в виде степенной (рис. 7а). На рис. 6б и рис. 7б приведены соответствующие графики функции g.
На основе испытаний алгоритма получена таблица эффективностей l путей, которые были определены выше, в зависимости от параметра с функции отталкивания e -cx (с для удобства реализации бралось равным (pm) -1, где m – величина шага движения):
| p | l |
| 1,124 | |
| 1,131 | |
| 1,135 | |
| 1,139 | |
| 1,143 |
Данные соответствуют среде, изображенной на рис. 6а. Из рисунка и таблицы видно, что для более гладких функций, задающих силу отталкивания, мы получаем и более гладкие траектории, однако величина l при этом возраста

