Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Московский государственный технический университет имени Н. Э. Баумана»
(МГТУ им. Н. Э. Баумана)
__________________________________________________________________
Факультет
«ИНЖЕНЕРНЫЙ БИЗНЕС И МЕНЕДЖМЕНТ»
Домашнее задание по дисциплине
«Прикладная статистика»
Вариант 5
Выполнила: студентка группы ИБМ7-41
Горх Д.И.
Москва, 2016
Часть 1
Задача 1
«Выборочные исследования. Проверка однородности двух независимых выборок»
Исходные данные:
В двух выборках присутствуют объекты, обладающие определенными свойствами. Объем первой выборки n1. Из них обладают рассматриваемым свойством k1.
Объем второй выборки n2. Из них обладают рассматриваемым свойством k2.
n1=909
n2=1278
k1=701
k2=872
Задание 1.1. Укажите доверительные границы для долей объектов в двух выборках, обладающих определенным свойством (с доверительной вероятностью 0.95)
1) n = 909
k = 701
P*=k/n=701/909=0.771
С(ɣ) = 1.96
Pниж = P* - С(ɣ)*√(P*((1-P*)/n))= 0.743
Pверх = P* + С(ɣ)*√(P*((1-P*)/n)) = 0.797
2) n = 1278
k = 872
P*=k/n=872/1278=0.682
С(ɣ) = 1.96
Pниж = P* - С(ɣ)*√(P*((1-P*)/n)) = 0.654
Pверх = P* + С(ɣ)*√(P*((1-P*)/n)) = 0.7056
Задание 1.2. Проверьте гипотезу о равенстве долей (уровень значимости α=0.05).
α=0.05 =>граничное значение k = 1.96
Н0: P1*=P2*
Гипотеза Н0 является ложной и между долями успехов в генеральных совокупностях существует значимая разница.
Н1: P1*≠ P2*
Гипотеза Н1 является альтернативной и между долями успехов в генеральных совокупностях не существует значимой разницы.
1) Вычислим статистику Q=(P1* - P2*)/(√(P1*(1-P1*)/n1) + √(P2*(1-P2*)/n2)), где P1* = k1/n1; P2* = k2/ n2
Q=(0.771-0.682)/(√ (0.771(1-0.771)/909) + √ (0.682 (1-0.682)/1278)) =3.296
|
|
2) Сравним значение модуля Q и значения k:
если Q ≤ k =>Н0
если Q>k =>Н1
В нашем случае 3.296> 1.96 т.е. Q > k => Н1P1*≠ P2*
Ответ: доли не равны.
Задача 2
«Средние величины. Показатели вариации»
Оценки за контрольную: 1088446105754486372864 9 86
Задание 2.1. Постройте вариационный ряд распределения оценок за задачу нужного номера. Произведите группировку и представьте результаты в табличной форме.
2;3;4;4;4;4;4;5;5;6;6;6;6;7;7;8;8;8;8;8;9;10;10
| Оценка, балл(xi) | ||||||||||
| Число учеников, чел (частота, fi) | ||||||||||
| Накопленная частота (fiн) |
Задание 2.2. По полученным данным определите:
а) средний балл за задачу (используя формулу взвешенного среднего),
б) моду,
в) медиану,
г) верхний, нижний квартили, межквартильное расстояние,
д) коэффициент и показатель асимметрии,
е) эксцесс.
Постройте ряд графически (полигон) и сформулируйте выводы о средних значениях и форме распределения.
а) средний балл за задачу:
= 
= 
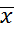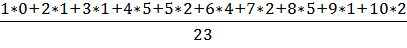= 6(6.174)
б) мода:
значение в ряду (xi), которому соответствует максимальная частота.
М = 4; 8
в) медиана:
xmed = x(k), k = (n-1)/2
k = 11
xmed =6
г) верхний, нижний квартили, межквартильное расстояние:
Нижний квартиль - Порядковая статистика с номером – целая часть от 0,25*n: x([0,25*n])
x(5) = 4
Верхний квартиль - Порядковая статистика с номером – целая часть от 0,75*n: x([0,75*n])
x(17) = 8
межквартильное расстояние:
Q = x(17) – x(5) = 4
д) коэффициент и показатель асимметрии:
Показатель асимметрии К. Пирсона: As= (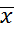 –M)/S =
|
|
= (6.174-4)/2.187 =0.994
As=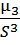 
= 
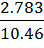= 0.266
Среднеквадратическое отклонение(S) =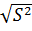 
= 2.187
Дисперсия(S2):S2= 
= 
=
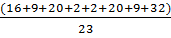= 4.783
е) эксцесс:
Ex= 
– 3 = 
– 3 = -0.92
µ4 = 
= 
= 47.565
2.3. Рассчитайте по построенному ряду показатели разброса (вариации):
а) среднее линейное отклонение,
б) дисперсию, среднеквадратическое отклонение,
в) коэффициент вариации.
По результатам расчетов сформулировать вывод о степени вариации и об однородности или неоднородности совокупности.
а) среднее линейное отклонение:
= 
= 
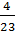= 0.174
б) дисперсию, среднеквадратическое отклонение:
Дисперсия(S2):S2= = =
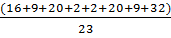= 4.783
Среднеквадратическое отклонение(S) = 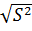= 2.187
в) коэффициент вариации:
Vn = 
*100% = 
= 36.45%
Степень вариации больше 33%(не умеренная), совокупность недостаточно однородная.