ТРИГОНОМЕТРИЧЕСКИЕ
УРАВНЕНИЯ И НЕРАВЕНСТВА
руководство к решению задач
содержание
ОСНОВНЫЕ ФОРМУЛЫТРИГОНОМЕТРИИ.. 5
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ.. 7
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ.. 8
Простейшие тригонометрические уравнения. 8
Тригонометрические уравнения. 11
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА.. 16
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
ОСНОВНЫЕ ФОРМУЛЫТРИГОНОМЕТРИИ
I. Основные тригонометрические тождества
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  .
. 
II. Формулы сложения
1.  ;
;
2.  ;
;
3.  ;
;
4.  .
.
5.  ;
;
6.  .
.
III. Формулы двойного аргумента
1.  ;
;
2.  ;
;
3. 
IV. Формулы преобразования произведения в сумму
1.  ;
;
2.  ;
;
3.  .
.
V. Формулы преобразования суммы в произведение
1.  ;
;
2.  ;
;
3.  ;
;
4.  .
.
VI. Знаки тригонометрических функций
 |
VII. Значения тригонометрических функций
| x | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
| sinx | -1 | 
| 
| 
| 
| 
| 
| 
| 
| 
| -1 | ||||
| cosx | 
| 
| 
| 
| 
| 
| 
| 
| 
| -1 | |||||
| tgx | - | 
| -1 | 
| 
| 
| - | 
| -1 | 
| - | ||||
| ctgx | 
| -1 | 
| - | 
| 
| 
| -1 | 
| - | - |
I. ОБРАтНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
(§3,П.8)
Функции, обратные тригонометрическим, называются соответственно арксинусом, арккосинусом, арктангенсом и арккотангенсом и обозначаются:
y = arcsin a, y = arccos a, y = arctg a, y = arcctg a.
Определения:
- Арксинусом числа а называется угол, заключенный в интервале  , синус которого равен а.
, синус которого равен а.
- Арккосинусом числа а называется угол, заключенный в интервале  , косинус которого равен а.
, косинус которого равен а.
- Арктангенсом числа а называется угол, заключенный в интервале  , тангенс которого равен а.
, тангенс которого равен а.
- Арккотангенсом числа а называется угол, заключенный в интервале  , котангенс которого равен а.
, котангенс которого равен а.
Пример 1. Вычислить:

Решение:
Пользуясь вышеперечисленными определениями и таблицей значений тригонометрических функций, получим:

Ответ: 
Пример 2. Вычислить:

Решение:
Опираясь на определения и таблицу значений тригонометрических функций, получим:

Ответ: 1
II. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
(§3,П.9,11)
Тригонометрическим уравнением называется равенство тригонометрических выражений, содержащих неизвестное (переменную) только под знаком тригонометрических функций.
Решить тригонометрическое уравнение, – значит, найти все его корни – все значения переменной, удовлетворяющие уравнению.
Решения тригонометрических уравнений сводятся к решению простейших тригонометрических уравнений, нахождение корней которых приведено в таблице:
ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ
УРАВНЕНИЯ
Таблица 1
| Вид уравнния | Формула решения тригонометрического уравнения | Частные случаи | |
| Вид уравнения | Формула решения тригонометрического уравнения | ||

|  или или

| 
| 
|

| 
| ||

| 
| ||

| 
| 
| 
|

| 
| ||

| 
| ||
  
| 
| ||

| 
| 
| 
|
Рассмотрим применение данной таблицы при решении простейших тригонометрических уравнений.
Пример 1. Решить уравнение:
 .
.
Решение:
Используя общую формулу для решения простейших тригонометрических уравнений относительно функции косинус, приведенную в таблице 1, получим:

Учитывая, что  , приходим к ответу
, приходим к ответу

Ответ: 
Пример 2. Решить уравнение:  .
.
Решение:
Сделаем замену переменной: пусть 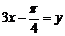 , тогда исходное уравнение примет вид:
, тогда исходное уравнение примет вид:

Используя частный случай простейшего тригонометрического уравнения относительно функции косинус (см.таблицу 1, стр7), получим:

Возвращаясь к исходной переменной, делаем обратную подстановку:

Выразим неизвестное х из полученного выражения, для этого необходимо перенести в правую часть равенства все слагаемые, не содержащие переменную, с противоположными знаками, а затем все выражение разделить на коэффициент, стоящий перед переменной х, получим:
 или
или 
откуда выражая х, получим: 
Ответ: 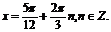
Пример 3. Решить уравнение:

Решение:
Приведем данное уравнение к простейшему тригонометрическому уравнению относительно функции синус:
 ,
,
откуда  .
.
Используя формулу для решения данного уравнения, приведенную в таблице, получим:
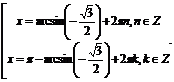
Учитывая, что  , имеем:
, имеем:

раскрывая скобки и приводя подобные члены во втором равенстве, окончательно получаем:



Ответ:

Решение более сложных тригонометрических уравнений требует знания формул тригонометрии, некоторые из них приведены в начале раздела.
Основные виды тригонометрических уравнений и способы их решений удобно представить в виде таблицы «Тригонометрические уравнения»:
Для решения тригонометрического уравнения необходимо правильно определить его вид, опираясь на левый столбец таблицы №2 и применить соответствующий способ решения уравнения, описанный в правом столбце таблицы.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Таблица 2
| № п/п | Вид уравнения | Способ решения |
| I. | Уравнения, приводящиеся к простейшим тригонометрическим уравнениям:
1.  2.
2. 
| Используются формулы:
1.  ,
2. ,
2. 

|
| II. | Квадратные тригонометрические уравнения:
1)  2)
2)  3)
3)  4)
4)  ,
где ,
где 
| Производится замена переменной:
1)   3) 3)  2)
2)   4) 4)  Уравнение сводится к квадратному относительно переменной у:
Уравнение сводится к квадратному относительно переменной у:
 после решения которого по формулам
после решения которого по формулам
 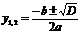 и обратной подстановки, исходное уравнение сводится к простейшему тригонометрическому уравнению.
и обратной подстановки, исходное уравнение сводится к простейшему тригонометрическому уравнению.
|
| III. | Уравнения, приводящиеся к квадратным:
1)  2)
2)  3)
3)  4)
4)  5)
5)  ,
где ,
где 
| Используются подстановки:
1)  ,
2) ,
2)  ,
3) ,
3)  или или  ,
4) ,
4)  ,
5) ,
5)  .
После приведения подобных членов, исходное уравнение сводится к квадратному тригонометрическому уравнению. .
После приведения подобных членов, исходное уравнение сводится к квадратному тригонометрическому уравнению.
|
Таблица 2 (Продолжение)
| № п/п | Вид уравнения | Способ решения |
| IV. | Неполные квадратные
уравнения:
1.  2.
2.  3.
3.  4.
4.  5.
5. 
| Общий множитель выносится за скобки:
 5.
5.  Каждый сомножитель приравнивается к нулю, уравнение сводится к совокупности двух простейших уравнений.
При решении уравнений вида (4) и (5) применяется формула синуса двойного угла:
Каждый сомножитель приравнивается к нулю, уравнение сводится к совокупности двух простейших уравнений.
При решении уравнений вида (4) и (5) применяется формула синуса двойного угла:
 . .
|
| V. | Однородные тригонометрические уравнения I-го порядка:

| Все уравнение делится на  и решается простейшее уравнение
и решается простейшее уравнение
 , , 
|
| VI. | Уравнения, приводящиеся к однородным тригонетрич-м уравнениям I-го порядка:
1. 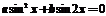 2.
2. 
| Используется формула:
 ,
после чего общий множитель (синус или косинус) выносится за скобку и каждый сомножитель приравнивается к нулю. Решение сводится к решению совокупности двух простейших уравнений. ,
после чего общий множитель (синус или косинус) выносится за скобку и каждый сомножитель приравнивается к нулю. Решение сводится к решению совокупности двух простейших уравнений.
|
| VII. | Однородные тригонометрические уравнения II-го порядка:

| Все уравнение делится на
 ,
уравнение сводится к квадратному, относительно функции тангенс: ,
уравнение сводится к квадратному, относительно функции тангенс:
 полученное уравнение решается при помощи формул, изложенных в этой таблице под номером IV пункт 3.
полученное уравнение решается при помощи формул, изложенных в этой таблице под номером IV пункт 3.
|
| VIII | Уравнения, приводящиеся к однородным тригонометр-м уравнениям II-го порядка:
1)  2)
2)  3)
3)  4)
4) 
| Используются формулы:
 или или  свободный коэффициент расписывается при помощи основного тригонометрического тождества:
свободный коэффициент расписывается при помощи основного тригонометрического тождества:
 или или  , где , где
 ,
т.е. ,
т.е. 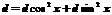 или или 
|
Приведенная выше таблица 2 далеко не исчерпывает все виды тригонометрических уравнений, это только маленькая часть из всего многообразия уравнений, чаще других встречающихся при изучении данного раздела.

Рассмотрим несколько примеров решения тригонометрических уравнений при помощи таблицы:
Пример 4. Решить уравнение:

Решение:
Пользуясь таблицей 2, легко определить, что данное уравнение – это уравнение, приводящееся к квадратному (см. III (5)), при помощи подстановки
 .
.
Получим:
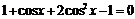 ,
,
после приведения подобных членов имеем:
 .
.
Получили неполное квадратное уравнение, для решения которого необходимо вынести общий множитель за скобки, после чего каждый сомножитель приравнять к нулю.

это уравнение равносильно совокупности двух уравнений:

Преобразуя второе уравнение, получим совокупность двух уравнений, решение которых приведено в таблице «Простейшие тригонометрические уравнения».
Получим:
 ;
; 
Ответ: 
Пример 5. Решить уравнение:

Решение:
Преобразуем данное выражение, применяя формулы двойного аргумента:

Получим:

Используя основное тригонометрическое тождество, имеем:

или

Раскрывая скобки в правой части уравнения и перенеся полученное выражение с противоположными знаками в левую часть уравнения, получим:

После приведения подобных членов исходное уравнение сводится к однородному тригонометрическому уравнению II-го порядка (таблица 2, VII):

или

Заметим, что если  , то из уравнения следует, что и
, то из уравнения следует, что и  , а это невозможно, так как в этом случае не выполняется основное тригонометрическое тождество
, а это невозможно, так как в этом случае не выполняется основное тригонометрическое тождество 
Так как значения х, при которых  , не являются корнями данного уравнения, то есть
, не являются корнями данного уравнения, то есть  , то все уравнение можно разделить на
, то все уравнение можно разделить на 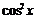 , получим:
, получим:

После сокращения и с учетом того, что  , имеем:
, имеем:

Решая данное квадратное тригонометрическое уравнение (таблица 2, II (3)), получим совокупность уравнений:

Применяя формулу решения простейших тригонометрических уравнений относительно функции тангенс, получим:
 ;
; 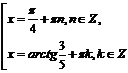
Ответ: 


