(§3,п.10)
Неравенства, содержащие переменную только под знаком тригонометрической функции, называются тригонометрическими.
Решить тригонометрическое неравенство, – значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется
Тригонометрические неравенства можно решать при помощи единичной окружности или с помощью графиков тригонометрических функций
y = sin x, y = cos x, y = tg x, y = ctg x.
Решение тригонометрических неравенств сводится, как правило, к решению простейших неравенств вида:
sin x < a, sin x > a, cos x < a, cos x > a,
sin x £ a, sin x ³ a, cos x £ a, cos x ³ a
и др.

 Рассмотрим решение простейших тригонометрических неравенств общего вида при помощи единичной окружности (радиус окружности равен единице). Центр единичной окружности совмещается с началом координат. При решении неравенств, относительно функции синус, необходимо провести прямую y = a; при решении неравенств, относительно функции косинус, проводится прямаяи x = a.
Рассмотрим решение простейших тригонометрических неравенств общего вида при помощи единичной окружности (радиус окружности равен единице). Центр единичной окружности совмещается с началом координат. При решении неравенств, относительно функции синус, необходимо провести прямую y = a; при решении неравенств, относительно функции косинус, проводится прямаяи x = a.
 |
 у=а
у=а
х=а
После чего выделяются точки пересечения прямой y=a (или x=a) с окружностью и выделяется дуга, содержащая все значения переменной х, для которой выполняется исходное неравенство. Решением неравенства является промежуток на оси Ох, включающий в себя координаты всех точек, спроецированных с выделенной дуги.
Общий вид решения простейших тригонометрических неравенств записывается с учетом периодичности функции
Представим данные неравенства и их решения в виде таблицы «Простейшие неравенства»:
ПРОСТЕЙШИЕ НЕРАВЕНСТВА
Решение простейших тригонометрических неравенств относительно функций y = tg x и y = ctg x удобно рассмотреть при помощи графиков данных функций.
Общий вид неравенств и их решений также представим в виде таблицы.
Таблица 3
| Вид неравенства | Общий вид решения неравенства |
| Sin x > a, -1 < a < 1 |
 
|
| Sin x < a, -1 < a < 1 |  
|
| Cos x > a, -1 < a < 1 | 

|
| Cos x < a, -1 < a < 1 | 

|
ПРОСТЕЙШИЕ НЕРАВЕНСТВА
Таблица 3 (продолжение)
| Вид неравенства |  Решение Решение
| ||||
tg x  a a
| 
| ||||
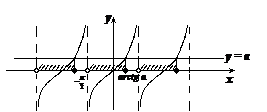
tg x  a a
| 

| ||||
ctg x  a a
| 
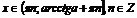
| ||||
ctg x  a a
| 
|
Рассмотрим некоторые примеры решения тригонометрических неравенств.
Пример 1. Решить неравенство:

Решение:
 На единичной окружности, центр которой совпадает с началом координат, проводим прямую
На единичной окружности, центр которой совпадает с началом координат, проводим прямую 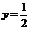 .
.
Все значения у на промежутке
CD (см.рис.1), больше  .
.

Отрезок CD является проекцией c
дуги АВ с началом в точке А  и концом в точке В
и концом в точке В 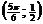 на ось Оу.
на ось Оу.
Рис 1
Из рисунка видно, что решением неравенства будут все значения, расположенные на дуге от точки А до точки В (обход против часовой стрелки), включая граничные точки, то есть

или
 , откуда
, откуда  .
.
Учитывая периодичность функции (Т=2p), получим все остальные решения неравенства добавлением к концам данного промежутка чисел вида 2p n, где n – целое число (т.е.  ).
).
Получим:

Ответ:

Пример 2. Решить неравенство:

Решение:
Для решения данного неравенства построим на одной координатной плоскости графики функций y = tg x и y = -1.
Отметим абсциссы точек пересечения данных графиков и выделим те промежутки значений х, при которых tg x > -1, то есть те значения, которым соответствуют точки графика, лежащие не ниже прямой у = -1.
 Один из таких промежутков
Один из таких промежутков  .
.
Учитывая периодичность тангенса (Т=p), нестрогий знак исходного неравенства (граничные точки должны войти в решение) и область определения функции тангенс, получим полуоткрытый интервал:

Ответ: 
Пример 3.
Решить неравенство:

Решение:
Данное неравенство – квадратное неравенство относительно функции синус.
Введем новую переменную: sin x = y, 
Тогда решение исходного неравенства сводится к решению квадратного неравенства:
 , (*)
, (*)
Разложим квадратный трехчлен на множители, для чего найдем корни квадратного уравнения, соответствующего исходному неравенству:


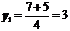 ,
, 
Применяя формулу разложения квадратного трехчлена на множители:
 , получим:
, получим:

Таким образом, неравенство (*) примет вид:
 (**)
(**)
Решим данное неравенство методом интервалов. Для этого отметим на числовой прямой точки, при которых неравенство (**) обращается в ноль, т.е. точки  . Данные точки разбивают числовую прямую на три интервала:
. Данные точки разбивают числовую прямую на три интервала:  . Определим знак выражения
. Определим знак выражения 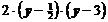 в каждом интервале. Для этого выбираем любые точки, принадлежащие каждому интервалу (например, 0; 1 и 5) и подставляем их по очереди в выражение
в каждом интервале. Для этого выбираем любые точки, принадлежащие каждому интервалу (например, 0; 1 и 5) и подставляем их по очереди в выражение 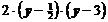 , знак полученного численного значения отмечаем в соответствующем промежутке на числовой прямой.
, знак полученного численного значения отмечаем в соответствующем промежутке на числовой прямой.
 |
Решением неравенства  являются промежутки, которые отмечены знаком плюс, включая граничные точки интервала (т.к. исходное неравенство имеет нестрогий знак: больше или равно нулю). Решением неравенства (**) является совокупность двух простейших неравенств:
являются промежутки, которые отмечены знаком плюс, включая граничные точки интервала (т.к. исходное неравенство имеет нестрогий знак: больше или равно нулю). Решением неравенства (**) является совокупность двух простейших неравенств:

Второе неравенство  не удовлетворяет области допустимых значений для переменной у. При вводе данной переменной в исходное неравенство на нее было наложено условие
не удовлетворяет области допустимых значений для переменной у. При вводе данной переменной в исходное неравенство на нее было наложено условие  . Так как у=3 не удовлетворяет данному условию, то решением неравенства (**) является условие
. Так как у=3 не удовлетворяет данному условию, то решением неравенства (**) является условие 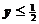
Возвращаясь к исходному неизвестному, получаем, что неравенство (**) равносильно простейшему тригонометрическому неравенству относительно функции синус:
 (***)
(***)
Для решения данного неравенства воспользуемся формулами, приведенными в таблице 1 (см. случай sin x < a), учитывая, что неравенство (***) нестрогое, получим:

или

откуда, после приведения подобных членов, получаем:

Ответ:

Пример4. Решить неравенство:
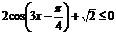
Решение:
Приведем неравенство к простейшему виду, для этого перенесем  в правую часть неравенства с противоположным знаком, затем полученное выражение разделим на 2, получим:
в правую часть неравенства с противоположным знаком, затем полученное выражение разделим на 2, получим:
 (*)
(*)
Введем новую переменную:
 ,
,
тогда неравенство (*) примет вид:
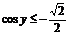 (**)
(**)
Для решения данного неравенства воспользуемся таблицей простейших неравенств (см. таблица 1, случай cos x < a), заменяя параметр а в данной формуле на отношение  и, учитывая, что исходное неравенство – нестрогое, получим:
и, учитывая, что исходное неравенство – нестрогое, получим:

Учитывая, что
 ,
,
получим:
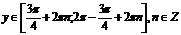
или

 .
.
Перейдем к переменной х, для этого выполним обратную подстановку, учитывая, что  , получим:
, получим:
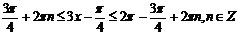 .
.
Для нахождения неизвестного х перенесем отношение  в левую и правую части неравенства с противоположным знаком, приведем подобные члены и разделим полученное выражение на 3 (коэффициент, стоящий перед переменной х), получим:
в левую и правую части неравенства с противоположным знаком, приведем подобные члены и разделим полученное выражение на 3 (коэффициент, стоящий перед переменной х), получим:


или

Ответ: 
