Рис. 4. Эквивалентное сечение плиты
Рабочая высота
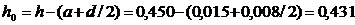 м,
м,
где а – защитный слой,
d - диаметр арматуры, принятый предварительно.
Толщина полки
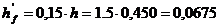 м.
м.
Ширина ребра
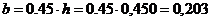 м.
м.
Расчетную ширину полки 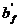 , поскольку
, поскольку 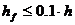 не выполняется, принимаем равной
не выполняется, принимаем равной 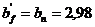 м
м
По назначенным расчетам сечения плиты и b определяем коэффициент
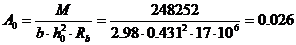 м2,
м2,
где Rb=17 МПа[4] – расчетное сопротивление сжатию бетона для класса В30.
В зависимости от А0, после интерполяции табличных значений находим η=0. 987, ξ=0.026 и вычисляем площадь сечения арматуры
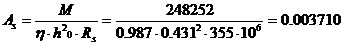 м2 =3710 мм2,
м2 =3710 мм2,
где Rs = 355 МПа – расчетное сопротивление растяжению арматуры класса АIII. Принимаем 8 стержней диаметром 25 мм, AII, с площадью As=3927 мм2.
Насыщение поперечных сечений панелей арматурой оценивают коэффициентом армирования
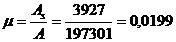 ,
,
где 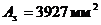 - площадь сечения арматуры,
- площадь сечения арматуры,
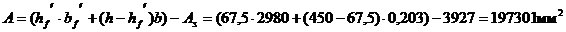 - площадь всего бетона в поперечном сечении.
- площадь всего бетона в поперечном сечении.
 Величина
Величина 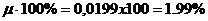 называется процентом армирования.
называется процентом армирования.
Предельный процент армирования для панелей определяется по формуле
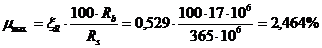 .
.
Минимальный процент армирования в панелях устанавливается из условия равнопрочности армированного сечения с неармированным и принимается равным 0.05% от 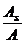 , т.е.
, т.е. 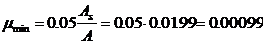 .
.
Фактический процент армирования выше минимального, поэтому расчет ведем с учетом арматуры.
Характеристика сжатой зоны бетона
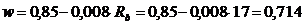 ,
, 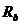 - в МПа.
- в МПа.
Граничная относительная высота сжатой зоны бетона
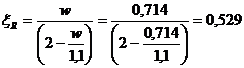 .
.
4 Расчет прочности по первой группе предельных состояний[1]
Целью расчета по первой группе предельных состояний является определение несущей способности панелей, тоопределение таких условий, при которых варматуре в сжатой зоне бетона никогда не будут достигнуты предельное состояние и связанная с нимопасность разрушения, потери устойчивости и др.
|
|
Расчет панелей производится:
а) по нормальному сечению элемента, то есть сечению, перпендикулярному к продольной оси, с целью определения площади сечения бетонаи площади поперечного сечения продольной арматуры;
б) по наклонному сечению на приопорных участках панели с целью
определения площади сечения поперечных и наклонных стержней.
Расчет прочности по нормальным сечениям
Расчет сечений плит выполняется по эквивалентному сечению в зависимости от положения нейтральной линии (рисунок 3), при этом встречаются два случая:
1)  нейтральная ось проходит в полке (рис. 3,а);
нейтральная ось проходит в полке (рис. 3,а);
2) нейтральная ось пересекает ребро (рис. 3,б).
     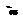 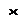 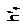 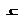 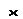   |
Рисунок 3. Форма сжатой зоны в расчетном сечении панели
а) при расположении границы сжатой зоны в полке;
б) при расположении границы сжатой зоны в ребре.
RSAS<RBbf’hf’
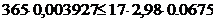
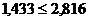 - условие выполняется, значит, расчет производится как для прямоугольного сечения шириной
- условие выполняется, значит, расчет производится как для прямоугольного сечения шириной 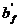 и проверяется выполнение условия прочности
и проверяется выполнение условия прочности
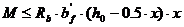
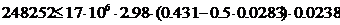
248252 Н·м 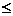 597628,67Н·м
597628,67Н·м
при этом высота сжатой зоны x определяется
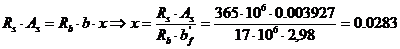 м.
м.
Условие прочности выполняется.
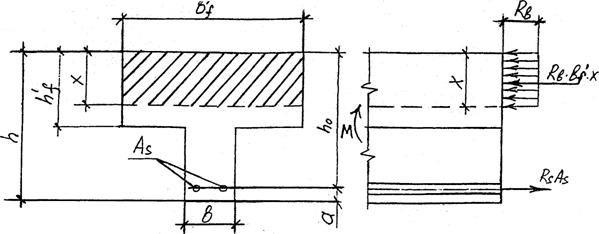
Рис. 4 - К расчету прочности по допускаемым напряжениям
Расчет прочности по наклонным сечениям
Опыты показывают, что наклонные трещины могут возникать вблизи опор панели в результате совместного действия изгибающего момента и поперечной силы.
Прочность наклонного сечения, определяемая работой бетона на растяжение, окажется достаточной, если
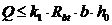 ,
,
где k1 = 0.6 – опытный коэффициент для тяжелого бетона.
 Rbt=1.2 МПа – расчетное сопротивление бетона на растяжение, для В30
Rbt=1.2 МПа – расчетное сопротивление бетона на растяжение, для В30
|
|
83.904 кН 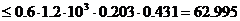 кН
кН
Условие прочности не выполняется. В элементе появляются наклонные трещины, и его прочность по наклонному сечению должна быть обеспечена арматурой, поставленной по расчету.
Требуемое усилие, воспринимаемое поперечными стержнями,
отнесенное к единице длины панели:
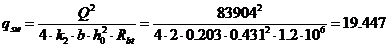 кН/м2.
кН/м2.
Проверяем выполнение условия:
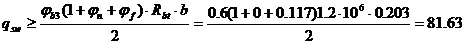 , кН/м2.
, кН/м2.
19,447≥81,63– условие не выполняется
где 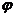 b3 – коэффициент, принимаемый равным для тяжелого бетона 0,6;
b3 – коэффициент, принимаемый равным для тяжелого бетона 0,6;
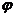 n – коэффициент, учитывающий влияние продольных сил, для панелей без предварительного напряжения арматуры равен 0;
n – коэффициент, учитывающий влияние продольных сил, для панелей без предварительного напряжения арматуры равен 0;
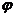 f – коэффициент, учитывающий влияние сжатых полок в тавровом сечении:
f – коэффициент, учитывающий влияние сжатых полок в тавровом сечении:
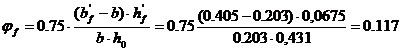 ≤0.5
≤0.5
 при этом bf’ ≤b+3hf’, принимаем bf’= 0.203+3·0.0675=0.405.
при этом bf’ ≤b+3hf’, принимаем bf’= 0.203+3·0.0675=0.405.
19,447≥81,63– условие не выполняется, следовательно, усилие в поперечных стержнях 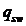 =81,3 кН/м
=81,3 кН/м
Rsw=290МПА – расчетное сопротивление растяжению поперечной и отогнутой по наклонному сечению на действие поперечной силы;
dw=8мм – диаметр поперечного стержня
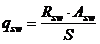
где S – шаг поперечной арматуры.
Asw=П  dw 2
dw 2  n/4=3,14
n/4=3,14  0,0082
0,0082  4/4=200мм2
4/4=200мм2
Вычислим значение S:
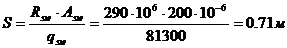 .
.
Для обеспечения прочности панелей по наклонному сечению необходимо, чтобы расчетные усилия М и Q не превышали несущей способности наклонного сечения, подсчитанной в зависимости от размеров поперечного сечения, его армирования, расчетного сопротивления бетона и арматуры.
Условие прочности имеет вид:
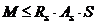 ,
,
248252<365  106
106  200
200  10-6
10-6  0.71
0.71
Условие прочности не выполняется.
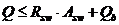 ,
,
где Qb – поперечное усилие, воспринимаемое бетоном:
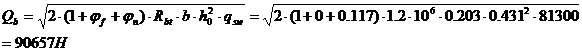
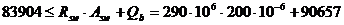
83,904 ≤ 148.657кН – условие выполняется.
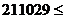
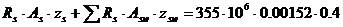
211029 ≤ 215840 кНм – условие выполняется
|
|
 5 Расчет панелей по предельным состояниям второй группы
5 Расчет панелей по предельным состояниям второй группы
При проектировании панели надо обеспечивать не только их прочность, но нужно также вести расчет по образованию и раскрытию трещин, а также по деформациям.
 5.1 Расчет по образованию трещин
5.1 Расчет по образованию трещин
Расчет панели выполняют по образованию трещин как нормальных, так и наклонных к продольной оси элемента.
По нормальным сечениям расчет производится из условия
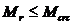 ,
,
где Mr – момент внешних сил, равный расчетному моменту от внешних усилий MII:
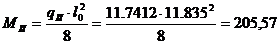 кН·м,
кН·м,
где 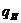 - нормативная нагрузка,
- нормативная нагрузка, 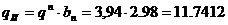 кН/м.
кН/м.
Mcrc - момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин:
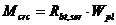 ,
,
где Wpl – момент сопротивления приведенного сечения для крайнего растянутого волокна
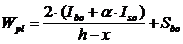 ,
,
где Ibo – момент инерции площадки сечения сжатой зоны бетона,
Iso – момент инерции площадки сечения арматуры в растянутой зоне,
Sbo – статический момент площадей сечения растянутой зоны бетона.
Rbt,ser=1.8 МПа, для бетона класса В30.
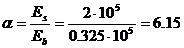
где α – коэффициент приведения,
Es=2·105 МПа, модуль упругости стали (арматура AIII),
Eb=0.325·105 МПа, модуль упругости бетона В30.
Расстояние от нулевой линии до крайнего растянутого волокна
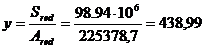 мм,
мм,
где Ared – площадь приведенного сечения
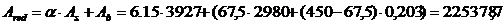 мм2,
мм2,
Sred – статический момент приведенного сечения
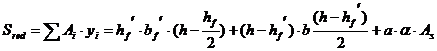 , м3.
, м3.
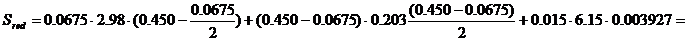
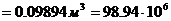 мм3.
мм3.
Вычисляем момент инерции площади сечения сжатой зоны бетона
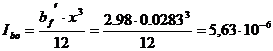 м4;
м4;
Вычисляем момент инерции площади сечения арматуры в растянутой зоне бетона
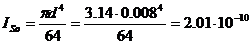 м4;
м4;
Вычисляем статический момент площади сечения растянутой зоны бетона 

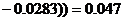 м4;
м4;
Подставляя найденные значения, получаем
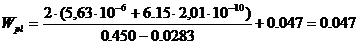 м3;
м3;
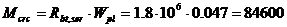 Н·м.
Н·м.
Mr= 205.57 кН·м 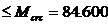 кН·м
кН·м
Условие не выполняется, образуются трещины, нормальные к продольной оси элемента, следовательно, необходимо проверить ширину их раскрытия.