РАБОЧАЯ ТЕТРАДЬ ПО ТЕМЕ 6.3
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Баранова Е.С.
Санкт-Петербург
Несобственные интегралы
В определении интеграла 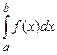 предполагалось, что: 1) промежуток интегрирования
предполагалось, что: 1) промежуток интегрирования 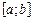 конечен; 2) функция
конечен; 2) функция 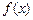 ограничена на отрезке
ограничена на отрезке 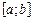 . Если нарушается хотя бы одно из условий 1) или 2), то интеграл называется несобственным.
. Если нарушается хотя бы одно из условий 1) или 2), то интеграл называется несобственным.
Несобственные интегралы с бесконечными пределами интегрирования
Если функция 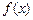 непрерывна на промежутке
непрерывна на промежутке  , то предел
, то предел 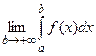 называется несобственным интегралом первого рода и обозначается
называется несобственным интегралом первого рода и обозначается
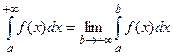 .
.
Если предел в правой части равенства существует и конечен, то несобственный интеграл называется сходящимся. Если же предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.
Если 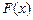 – первообразная для подынтегральной функции
– первообразная для подынтегральной функции 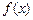 , то
, то
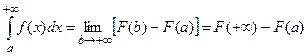 ,
,
где 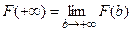 .
.
замечание
Если функция 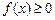 и непрерывна на промежутке
и непрерывна на промежутке  и интеграл
и интеграл 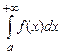 сходится, то этот несобственный интеграл равен площади криволинейной трапеции, которая бесконечно простирается влево вдоль оси Ох (рис. 17).
сходится, то этот несобственный интеграл равен площади криволинейной трапеции, которая бесконечно простирается влево вдоль оси Ох (рис. 17).

Рис. 17.
Аналогичным образом определяется интеграл на промежутке  :
:
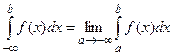 .
.
Несобственный интеграл с двумя бесконечными пределами интегрирования разбивается на сумму двух интегралов:
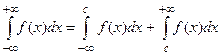 ,
,
где 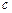 – произвольное число, причем интеграл в левой части равенства сходится при условии, что оба интеграла в правой части сходятся.
– произвольное число, причем интеграл в левой части равенства сходится при условии, что оба интеграла в правой части сходятся.
Пример 1. Вычислить интеграл 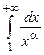 , где
, где 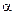 – некоторое число.
– некоторое число.
Решение.
1) Если 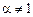 , то
, то 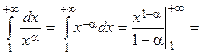
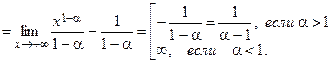 .
.
2) Если 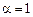 , то
, то 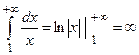
Таким образом, интеграл 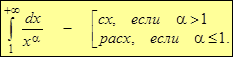
Признаки сходимости несобственных интегралов первого рода
Теорема 1 (признак сравнения). Если для всех 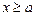 непрерывные функции
непрерывные функции 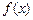 и
и 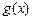 удовлетворяют неравенству
удовлетворяют неравенству 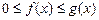 и
и
1) если интеграл 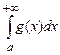 сходится, то интеграл
сходится, то интеграл 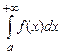 тоже сходится, причем
тоже сходится, причем 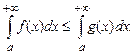
2) если же интеграл 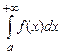 расходится, то интеграл
расходится, то интеграл  тоже расходится.
тоже расходится.
Пример 2. Исследовать сходится ли интеграл 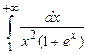 ?
?
Решение. Так как при  выполняется неравенство
выполняется неравенство 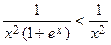 и
и 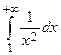 сходится (
сходится (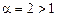 ; см. пример 1), то данный интеграл сходится.
; см. пример 1), то данный интеграл сходится.
Теорема 2. Если интеграл 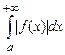 сходится, то сходится и интеграл
сходится, то сходится и интеграл  . В этом случае последний интеграл называется абсолютно сходящимся.
. В этом случае последний интеграл называется абсолютно сходящимся.
Пример 3. Исследовать сходимость интеграла  .
.
Решение. Так как 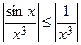 и интеграл
и интеграл 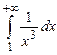 сходится, то данный интеграл сходится абсолютно.
сходится, то данный интеграл сходится абсолютно.
Теорема 3 (предельный признак сравнения). Если для всех  функции
функции 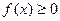 и
и 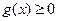 , причем
, причем 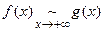 , то интегралы
, то интегралы 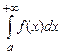 и
и  одновременно оба сходятся или одновременно оба расходятся (т.е. ведут себя одинаково в смысле сходимости).
одновременно оба сходятся или одновременно оба расходятся (т.е. ведут себя одинаково в смысле сходимости).
Пример 4. Исследовать сходимость интеграла 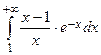 .
.
Решение. Интеграл 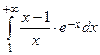 сходится, так как
сходится, так как
1) 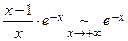 ;
;
2) интеграл 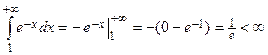 – сходится.
– сходится.
Пример 5. Исследовать сходимость интеграла 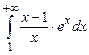 .
.
Решение. Интеграл  расходится, так как
расходится, так как
1) 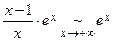 ;
;
2) интеграл 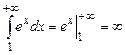 – расходится.
– расходится.
Несобственные интегралы от разрывных функций
Если функция 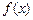 непрерывна при
непрерывна при 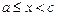 и имеет бесконечный разрыв в точке
и имеет бесконечный разрыв в точке 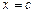 , то предел
, то предел 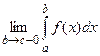 называется несобственным интегралом второго рода и обозначается
называется несобственным интегралом второго рода и обозначается
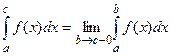 .
.
Если предел в правой части существует и конечен, то несобственный интеграл называется сходящимся. Если же предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.
Замечание.
Если функция  и имеет бесконечный разрыв в точке
и имеет бесконечный разрыв в точке 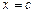 и интеграл
и интеграл 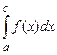 сходится, то этот несобственный интеграл равен площади криволинейной трапеции, которая бесконечно простирается вверх вдоль прямой
сходится, то этот несобственный интеграл равен площади криволинейной трапеции, которая бесконечно простирается вверх вдоль прямой 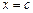 (рис. 18).
(рис. 18).
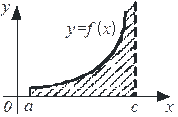
Рис. 18.
Аналогично определяются интегралы:
1) Если функция 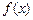 непрерывна при
непрерывна при  и терпит разрыв в точке с, то
и терпит разрыв в точке с, то
 .
.
2) Если функция 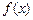 непрерывна при
непрерывна при 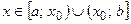 и терпит бесконечный разрыв в точке
и терпит бесконечный разрыв в точке 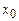 , то
, то
 .
.
В этом случае интеграл слева называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.
Пример 6. Вычислить интеграл  , где
, где 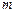 – некоторое число.
– некоторое число.
Решение.
1) Если 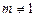 , то
, то
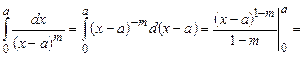
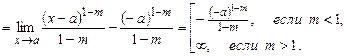
2) Если 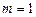 , то
, то 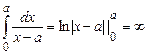 .
.
Таким образом, интеграл