Проводники в электрическом поле.

ЭЛЕКТРОМАГНЕТИЗМ

Глава 2. Электростатика в веществе.

Проводники в электрическом поле.

2.5.1. Проводники.

 

Наиболее хорошими проводниками электричества являются металлы. Основные особенности проводников состоят в следующем:

1) В проводниках имеются свободные заряды, т.е. индуцированные заряды разделяются (могут быть разделены механически); в металлах свободными зарядами являются электроны.

2) В равновесном состоянии электрическое поле внутри проводника, находящегося во внешнем поле или заряженного до некоторого значения 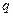, равно нулю ().

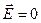В противном случае на электрические заряды в проводнике будет действовать со стороны поля сила, приводящая их в движение и вызывающая перераспределение зарядов. В электростатическом состоянии движение зарядов отсутствует, откуда следует, что электрическое поле внутри проводящего вещества должно быть равно нулю. Отсюда неизбежно получаем, что в стационарном состоянии в проводнике

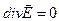
и, следовательно, объемная плотность 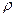избыточных (нескомпенсированных) зарядов внутри однородного проводника также равна нулю.

Заметим, что мы имеем в виду поле, усредненное по объему, который велик по сравнению с характерными объёмами атомов.

3) Избыточный электрический заряд может располагаться только на поверхности проводника с некоторой

плотностью 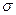, вообще говоря, различной в разных точках его поверхности. Избыточный поверхностный

заряд находится в очень тонком слое у поверхности проводника (толщина слоя порядка одного – двух межатомных расстояний).

4) Отсутствие поля внутри проводника (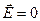), означает, что потенциал в объеме проводника одинаков во всех точках: 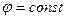, т.е. проводник представляет собой эквипотенциальную область пространства, а его поверхность – эквипотенциальную поверхность.

5) Напряженность поля 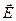в любой точке поверхности проводника направлена перпендикулярно к ней (иначе на поверхности проводника будут происходить движение зарядов до тех пор, пока не обратится в нуль тангенциальная составляющая поля 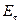), т.е. .

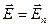Т.о., в состоянии равновесия тангенциальная составляющая поля 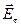внутри и вне проводника должна быть равна нулю.

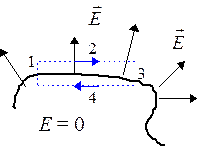
Доказательство этого утверждения можно провести, используя теорему о циркуляции для вектора 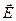и выбрав для этой цели контур 1-2-3-4, как показано на рисунке:

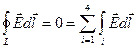(5.1)

Стороны 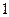и 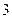контура можно сделать сколь угодно малыми, вследствие чего интегралы по ним обращаются в нуль. Нулю также равен интеграл, взятый по участку контура 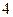, поскольку поле внутри проводника равно нулю. Тогда при интегрировании по стороне 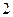контура в силу (5.1) имеем 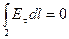. Поскольку сторона два может быть выбрана любой (малой) длины, то получаем, что .

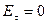6) Поле вблизи поверхности проводника. Пусть интересующий нас участок поверхности проводника граничит с вакуумом (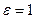). Линии вектора 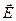перпендикулярны поверхности проводника, поэтому в качестве замкнутой поверхности возьмем небольшой цилиндр, расположив его, как показано на рисунке. Теорему Гаусса для выбранной цилиндрической поверхности, вырезающей на поверхности проводника площадку 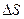с плотностью стороннего заряда 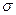, можем записать в виде:

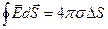. (5.2)

Т.к. через нижнее основание и боковую поверхность поток вектора 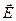(из-за 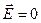внутри проводника и 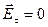) равен нулю, то

,

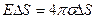или

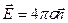. (5.3)

В СИ: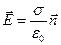

Дополнение

Скачок нормальной составляющей вектора на поверхности проводника 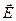можно (полезно) объяснить, используя другой подход – рассматривая суперпозицию полей. Полное поле, описываемое вектором 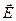, складывается из электрического поля 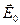, создаваемого зарядами, расположенными на маленькой площадке 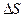, которую можно выделить на поверхности, и поля 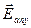, возбуждаемого всеми остальными зарядами, находящимися на рассматриваемой поверхности. Мысленно удалим с поверхности площадку 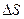. Тогда внешнее по отношению к ней поле 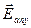изменяется в “дырке” - непрерывно (см. рисунок). Поле 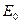(у поверхности) находится по т. Гаусса как поле бесконечной равномерно заряженной плоскости, равно 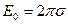и направлено, как показано на рисунке.

Тогда в силу принципа суперпозиции поля по обе стороны поверхности равны, соответственно:

(5.4)

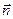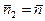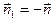Вводя общую внешнюю нормаль ( и ), получаем, что при переходе поверхности электрическое поле изменяется скачком на величину:

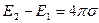. (5.5)

 

2.5.2. Метод электрических изображений.

 

Пусть имеется плоская проводящаяся поверхность, простирающаяся в бесконечность. Припишем этой плоскости нулевой потенциал. Расположим теперь точечный заряд 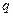над плоскостью на оси 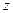на расстоянии 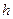вблизи её поверхности. Поверхностную плотность наведенного (индуцированного) заряда 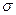и поле вблизи проводящей поверхности можно вычислить двумя способами.

1) Мы предполагаем, что положительный заряд 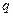будет индуцировать на поверхности отрицательный заряд, плотность которого 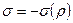меняется с расстоянием 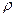(отсчет ведется от точки на плоскости, куда проецируется заряд – см. рисунок). Очевидно, что картина должна быть симметричной относительно оси .

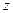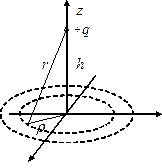
Напряженность результирующего поля определяется как векторная сумма напряженностей полей, создаваемых точечным зарядом 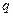и наведенным зарядом, распределенным по плоскости с плотностью 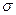, причем нормальные составляющие векторов 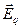и 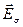в полупространстве над плоскостью складываются, а под поверхностью - вычитаются, причем так, что поле в нижнем полупространстве равно нулю.

Используя соотношения (5.3) и (5.4), получаем для нормальной компоненты поля (тангенциальные, как было показано выше, равны нулю) над плоскостью:

 

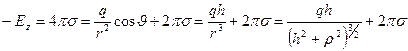. (5.6)

Знак “– “ в выражении (5.6) указывает на то, что направление нормальной компоненты вектора напряженности электрического поля вблизи плоскости противоположно оси .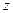

Соответственно, в нижнем полупространстве:

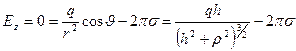. (5.7)

Складывая два последних выражения, находим напряженность поля и поверхностную плотность заряда:

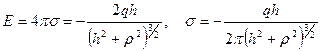. (5.8)

Если мы просуммируем заряд, индуцированный на плоскости, то получим заряд “ 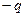”. В самом деле:

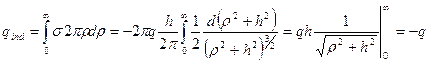(5.9)

2) Результат, полученный в (5.9), приводит к весьма любопытным выводам. Оказывается, что то же электрическое поле можно получить, заменив плоскость с распределенными на ней наведенными зарядами точечным зарядом 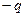, помещенным на оси 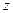на расстоянии 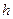(см. рисунки) в нижнем полупространстве. Действительно, вблизи поверхности получаем

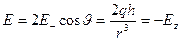(5.10)

В этом методе – “методе изображений” – результирующее поле в любой точке “ верхнего” полупространства находится как сумма полей от «истинного» и «фиктивного» зарядов:

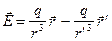. (5.11)

Особо подчеркнем, что “действие”, фиктивного заряда 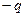распространяется лишь на то полупространство, в котором находится действительный заряд 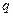. В “ нижнем ” полупространстве поле отсутствует.

Рассмотренный в пункте 2) способ расчета – это искусственный метод для расчета взаимодействия проводников с зарядами и другими полями, позволяющий в ряде случаев (весьма ограниченном) рассчитать электрическое поле достаточно просто.

В общем случае идея предложенного метода формулируется следующим образом.

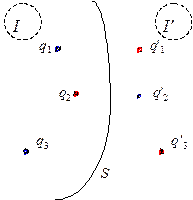
Пусть имеется система точечных зарядов и пусть 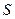– эквипотенциальная поверхность, разделяющая пространство на два полупространства 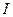и 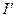(см. рис). Задание зарядов 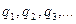и потенциала на поверхности 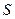однозначным образом определяет электрическое поле в полупространстве 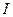и, аналогично, в полупространстве .

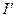По теореме единственности (уравнение 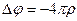имеет единственное решение) поле определяется однозначно. Поэтому, если сделать поверхность 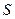проводящей, то поле во всем пространстве не изменится, т.к. поля в подпространствах 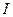и 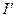независимы. Тогда поле в полупространстве 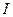можно получать двумя эквивалентными способами:

1) либо как сумму полей, создаваемых зарядами 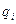и зарядами, наведенными на поверхности ;

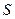2) либо как сумму полей, создаваемых зарядом 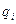и «фиктивным» зарядом 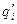, имея при этом в виду, что поле фиктивного заряда распространяется только на то полупространство, в котором находится действительный заряд.

По существу. рассматриваемый метод основан на подгонке потенциала под граничные условия: мы стараемся подобрать такую конфигурацию фиктивных зарядов, у которой конфигурация поля в интересующей нас части пространства была бы той же. Если этого удается достичь с помощью достаточно простой конфигурации, то метод изображений оказывается весьма эффективным.

Совокупность зарядов 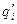рассматривается как «зеркальное изображение» электрических зарядов 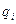в проводнике, ограниченном поверхностью 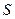. Отсюда способ расчета взаимодействия зарядов с проводниками и полей вблизи проводников получил название «метод электрических изображений».

Применение метода электрических изображений для решения определенного круга задач электростатики обосновано теоремой единственности: поскольку полученное таким решение задачи удовлетворяет уравнению Пуассона и граничным условиям, то оно является правильным и единственным.

 

2.5.3. Емкость проводников.

 

Если проводнику сообщить заряд 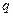, то он распределяется по поверхности проводника единственным способом, причем так, чтобы внутри проводника поле было равно нулю, а потенциал постоянен. Такое распределение будет сохраняться, когда проводник уединенный, т.е. когда поблизости нет других тел, заряды которых или поляризация могут вызвать перераспределение зарядов на интересующем нас проводнике.

Итак, рассмотрим уединенный заряженный проводник. Если увеличить его заряд на 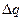, то он распределится аналогичным образом, лишь возрастет напряженность поля вблизи поверхности и потенциал проводника. Опыт показывает, что между зарядом проводника и его потенциалом существует прямая пропорциональность (потенциал на бесконечности считаем равным нулю):

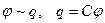. (5.12)

Коэффициент пропорциональности 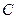называют электроемкостью или емкостью уединенного проводника.

Емкость зависит от размеров и формы проводника. Она численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу.

Пример: Пусть проводящий уединенный шар имеет радиус 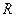. Найдем потенциал этого шара

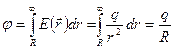или 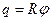. (5.13)

Тогда емкость проводящего шара равна

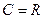. (5.14)

Единица емкости в системе 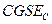(Гаусса): .

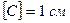Примечание: в СИ имеем 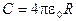и единица емкости 1 Фарада:

.

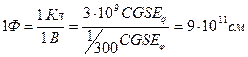Фарада - очень большая величина, так 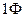- это емкость шара радиусом 9×10⁹ м, что в 1500 раз больше радиуса Земли (емкость Земли 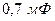). Поэтому для практических нужд вводят обычно кратные величины: .

 

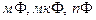2.5.4. Конденсаторы.

 

Наличие вблизи проводника других тел изменяет его электрическую емкость, т.к. потенциал проводника зависит и от электрических полей, создаваемых зарядами, наведенными в окружающих телах вследствие электростатической индукции. При приближении к заряженному проводнику других тел в них будет происходить перераспределение зарядов, причем так, что ближе окажутся заряды противоположные по знаку заряду рассматриваемого проводника. Поэтому потенциал проводника, являющийся алгебраической суммой потенциалов собственных и индуцированных на других телах зарядов, уменьшится, а, значит, его емкость увеличится.

Конденсатором называют систему, состоящую из двух проводников, отделенных слоем диэлектрика, расстояние между которыми много меньше их линейных размеров.

Чтобы внешние поля не оказывали заметного влияния на емкость конденсатора, нужно, чтобы поле, создаваемое накапливающимися на обкладках зарядами, было практически полностью сосредоточено внутри конденсатора. Другими словами, линии вектора 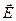, начинающиеся на одной обкладке (проводнике), должны заканчиваться на другой, что выполняется, если заряды на обкладках равны по величине и противоположны по знаку. В реальном конденсаторе это условие выполняется приближенно, но с достаточно хорошей точностью.

Заряд конденсатора (заряд, расположенный на одной из его обкладок), связан с разностью потенциалов между обкладками конденсатора через коэффициент пропорциональности - емкость конденсатора:

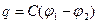. (5.15)

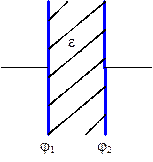
Емкость зависит от конструкции конденсатора. Наиболее простыми и часто используемыми являются плоский, цилиндрический и сферический конденсаторы. Рассмотрим их устройство и характеристики.

 

1). Плоский конденсатор: две параллельные проводящие пластинки, между которыми расположен тонкий диэлектрик с диэлектрической проницаемостью 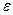. Расстояние между пластинами конденсатора 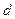, площадь пластин равна 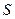. Напряжение на конденсаторе:

.

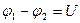Электрическое поле внутри конденсатора мы рассматриваем как суперпозицию полей двух бесконечных разноименно заряженных плоскостей:

.

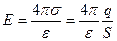Т.о., поле в плоском конденсаторе – однородное.

Отсюда находим связь между напряжением на конденсаторе и его электрическим полем:

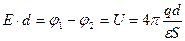
и емкость плоского конденсатора:

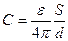. (5.15)

Примечание: в СИ емкость плоского конденсатора .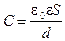

2). Сферический конденсатор: две проводящие концентрические сферы, радиусам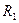и и 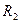(обкладки конденсатора), разделенные тонким слоем диэлектрика с диэлектрической проницаемостью 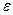. Разность потенциалов определяется из соотношения

,

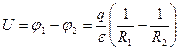откуда находим емкость сферического конденсатора

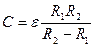(5.16)

Примечание: в СИ емкость сферического конденсатора

.

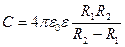3). Цилиндрический конденсатор: обкладками конденсатора служат два проводящих коаксиальных цилиндра радиусам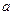и и 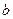, между которыми расположен тонкий диэлектрик с диэлектрической проницаемостью 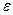. Длина цилиндров равна 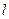(при этом 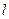достаточно велико: 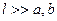). Поле внутри цилиндрического конденсатора (между цилиндрами) легко найти, используя теорему Гаусса (см. Глава 1, §3, формула (3.7)):

,

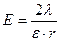где 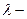заряд, приходящийся на единицу длины одного из цилиндров. Тогда разность потенциалов между обкладками цилиндрического конденсатора:

.

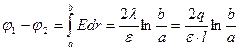Следовательно, емкость цилиндрического конденсатора:

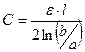. (5.17)

Примечание: в СИ емкость цилиндрического конденсатора: 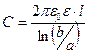.