Как указывалось выше в настоящее время используются только связанные многофазные системы, в которых обмотки генератора должны соединяться между собой и с нагрузкой. В трехфазных цепях существуют два основных способа соединения обмоток генераторов, трансформаторов и приемников: звезда (۸) и треугольник (D). При соединении в ۸ (рис.4.3) все концы фазных обмоток генератора соединяются в общую точку (в связи с этим обычно буквы X, Y, Z не наносят). Точно так же в ۸ можно соединить сопротивления приемника. Общие точки обмоток генератора (0) и ветвей приемника (01) называются их нулевыми или нейтральными точками, а соединяющий их провод (если он есть) называется нулевым или нейтральным проводом. Остальные провода, соединяющие обмотки генератора с приемником, называются линейными.
|
Схемы соединения обмоток генератора и сопротивлений приемника не зависят друг от друга, поэтому существует 5 схем соединения в трехфазных цепях: ۸--۸ (рис.4.3); ۸ ۸; ۸ D; D ۸ и D D (рис.4.4). Лучи звезды и ветви треугольника приемника называются фазами приемника, асопротивления фаз приемника – его фазными сопротивлениями.
|
|
Все величины, относящиеся к фазам, принято называть фазными (фазная ЭДС Е ф, фазное напряжение U ф, фазный ток I ф и т.д.). Все же величины, относящиеся к линейным проводам, принято называть линейными (линейное напряжение U л, линейны ток I л и т.д.). Следует иметь в в иду, что при соединении в ۸ I ф = I л, а при соединении в D U ф = U л.
В трехфазных цепях принято выбирать следующие положительные направления величин: ЭДС и токов в ветвях источников – от концов обмоток к началам; токов в линейных проводах – от источника к приемнику; тока в нулевом проводе – от 01 к 0; напряжений и токов в ветвях треугольника приемника – в направлении А-В-С-А.
Различают симметричные и несимметричные трехфазные цепи. Цепь симметрична, если комплексные сопротивления каждой из фаз одинаковы. В противном случае цепь несимметрична. Если к симметричной цепи подвести симметричную же систему напряжений, то система токов также будет симметричной и такой режим работы цепи называется симметричным.
Симметричный режим работы трехфазной цепи
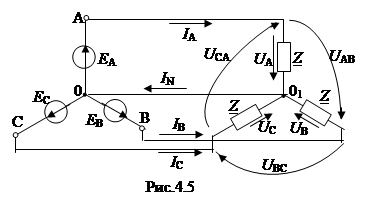Рассмотрим симметричный режим в схеме ۸--۸ (рис.4.5). Так как точки 0 и 01 соединены, то нет напряжения между этими точками, поэтому
U A= E A; U B= E B; U C= E C и токи
I A= U A/ Z; I B= U B/ Z; I C= U C/ Z.
Ток в нулевом проводе
I N= I A+ I B+ I C=0, так как система токов I A, I В, I С, что вытекает из векторной диаграммы, приведенной на рис.4.6. В связи с этим в симметричном режиме нулевой провод не применяют.
Линейные напряжения при положительных направлениях, указанных на рис.4.5, в соответствии со вторым законом Кирхгофа определяются как разности фазных напряжений:
|
|
U AB= U A- U B; U BC= U B- U C; U CA= U C- U A.
По модулю все линейные напряжения одинаковы. Соотношение между линейными и фазными напряжениями, которые также одинаковы по величине, определим из треугольника CD0, в котором катет CD представлет собой половину линейного напряжения, а гипотенузой является фазное напряжение. Тогда
0.5 U л= U фcos30º= U ф0.5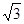 
или
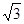U л= U ф.
При соединении приемника по схеме D (рис.4.6) к сопротивлениям последнего непосредственно подводятся линейные напряжения, поэтому по закону Ома
I AB= U AB/ Z; I BC= U BC/ Z; I CA= U CA/ Z,
а по первому закону Кирхгофа
I A= I AB- I СА; I В= I BС- I АВ; I С= I СА- I ВС.
На основании этих формул построена векторная диаграмма (рис.4.7) для случая, когда φ<0. Из этой диаграммы следует, что все линейные токи (как и фазные) по величине одинаковы, причем I л= 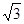I ф.
Активная мощность симметричного трехфазного приемника
P =3 U ф I фcosφ.
Учитывая, что при соединении звездой I ф= I л и U л= 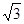U ф, а при соединении треугольником U ф= U л и I л= 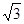I ф, не зависимо от схемы соединения приемника, получим
P = 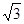U л I лcosφ.
Аналогично для реактивной и полной мощностей симметричного трехфазного приемника имеем
Q =3 U ф I фsinφ= 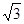U л I лsinφ; S =3 U ф I ф= 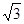U л I л.
Следует помнить, что в этих формулах φ– это сдвиг по фазе между фазным напряжением и фазным током.
Расчет трехфазных цепей
Трехфазные цепи представляют собой разновидность сложных цепей синусоидального тока и поэтому в принципе их расчет производится ранее рассмотренными методами и приемами. Однако для трехфазных цепей имеется ряд важных особенностей, облегчающих их расчет и исследование. Рассчитываются трехфазные цепи со статической нагрузкой, т.е. не содержащей электродвигателей, трансформаторов и др. активных элементов, как правило комплексным методом. Их расчет обычно сопровождается построением векторных или топографических диаграмм, которые предостерегают от возможных ошибок аналитических расчетов, делают все соотношения более наглядными, облегчают определение углов сдвига по фазе между любыми величинами.
|
|
Расчет симметричных трехфазных цепей
Сначала рассмотрим схему звезда-звезда без нулевого провода (рис.4.8). Это сложная цепь, имеющая два узла, и её расчет проще всего произвести методом узлового напряжения. В трехфазных цепях узловое напряжение U 010 получило специальное название – смещение нейтрали.
.
Здесь Y =1/ Z, а ноль получается потому, что Е А, Е В и Е С образуют симметричную систему. Так как разности потенциалов между точками 01 и 0 нет, то их можно соединить не нарушая работы схемы. Тогда каждую фазу можно рассматривать отдельно. Поскольку все фазы совершенно одинаковы (имеют одинаковые сопротивления и величины ЭДС), то нет необходимости рассчитывать токи во всех фазах, а достаточно сделать это для одной только фазы, например, I A= E A/ Z. Токи в других фазах будут точно такими же, только сдвинутыми на 120˚ толи в сторону отставания, толи в сторону опережения.
С расчетом более сложных симметричных цепей познакомимся на примере схемы рис.4.9,а. Для выполнения расчета проще всего все соединения треугольником заменить на соединение звездой. Напомним, что фазное напряжение меньше линейного в 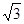раз, а сопротивление эквивалентной звезды в 3 раза меньше сопротивления заменяемого треугольника, т.е. Z `4= Z 4/3. После указанного преобразования получим схему рис.4.9,б. Так же как и для схемы рис.4.8 можно показать, что все нулевые точки (0, 01,02) имеют одинаковый потенциал, поэтому их можно соединить не нарушая режима работы схемы. Затем можно удалить 2 фазы, например, В и С и получить схему одной фазы (рис.4.10), токи в которой легко рассчитать её дальнейшего преобразования, а именно
Токи в фазах В и С такие же как и в фазе А, но по фазе сдвинуты на 120˚ в сторону отставания и опережения соответственно. Величины токов в ветвях треугольников определяются путем деления на 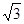соответствующих линейных токов, например, I 4ф= I 3А/ .
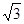Расчет несимметричных трехфазных цепей
Расчет таких цепей рассмотрим на конкретных примерах. В схеме звезда-звезда без нулевого провода (рис.4.11,а) задана система симметричных или несимметричных фазных напряжений U A, U B, U C, приложенных к зажимам несимметричного приемника Z A≠ Z B≠ Z C. Требуется определить токи. Заданные напряжения можно приписать источникам ЭДС (рис.4.11) E A= U A; E B= U B; E C= U C. В схеме два узла, поэтому целесообразно применить метод узлового напряжения. Обозначим напряжение между нулевыми точками приемника и источника (смещение нейтрали) через U 0`0= U N, тогда
 |
где Y A, Y B, Y C - комплексные проводимости ветвей. Токи определяем по закону Ома
Кроме того I N= I A+ I B + I C. Последнее соотношение как правило используют для проверки правильности расчета токов. На рис.4.11,б показан примерный вид векторной (топографической) диаграммы цепи для случая, когда φА>0, φB<0 и φС=0.
Рассмотрим частные случаи. Когда нулевой провод не имеет сопротивления (Z N=0, Y N=∞) получаем U N=0 и, следовательно напряжения на фазах приемника равны фазным напряжениям источника питания. В этом случае ток в каждой фазе определяется по закону Ома и не зависит от токов других фаз, а I N= I A+ I B + I C. На рис.4.12 показан примерный вид векторной (топографической) диаграммы цепи для этого случая. Заметим, что в этом случае величины напряжений на фазах несимметричного приемника становятся одинаковыми (отсутствует так называемый перекос фаз), что в ряде случаев крайне необходимо, например для бытовых электроприемников, питающихся от разных фаз. Можно сказать, что назначение нулевого провода (при Z N=0) – это ликвидировать смещение нейтрали.
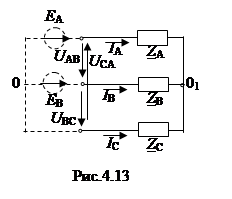Еще одним частным случаем является отсутствие нулевого провода (Z N=∞, Y N=0). Тогда расчет производится совершенно аналогично самому первому случаю, только изменяется выражение для U N из-за того, что Y N=0. Аналогично рвсчитываются и токи, только I A+ I B + I C =0. Векторная диаграмма имеет вид, аналогичный рис.4.11,б, только I A+ I B + I C =0. Обычно при отсутствии нулевого провода не фазные напряжения (их негде мерять), а линейные. В случае симметричной системы линейных напряжений, по ним можно определить фазные и далее производить расчет как указано выше. Если же система линейных напряжений несимметрична, то такой возможности нет и тогда расчет производят так. С учетом того, что в соответствии со вторым законом Кирхгофа для контура, образованного линейными напряжениями, U AB+ U BC+ U CA=0, систему этих напряжений можно приписать только двум ЭДС, например так как показано на рис.4.13, причем Е А=- U CA= U AC, а Е В= U ВС. Тогда узловое напряжение и токи
.
Проверка обычно производится по выражению I A+ I B + I C =0.
Рассмотрим далее расчет схемы несимметричного треугольника (рис.4.14,а). Линейные напряжения U AB, U BC и U CA известны или могут быть определены, а рассчитать нужно токи.
 |
Поскольку линейные напряжения непосредственно воздействуют на сопротивления приемника, то токи в ветвях треугольника определяем по закону Ома, а линейные токи – с помощью первого закона Кирхгофа
I A= I AB- I СА; I В= I BС- I АВ; I С= I СА- I ВС.
Примерный вид векторной диаграммы цепи (при φА>0, φB<0 и φС=0) показан на рис.4.14,б.
Существенно сложнее расчет схемы рис.4.15, в которой заданы фазные или линейные напряжения источника питания и все сопротивления, а определить нужно все токи. Проще всего задача решается, если треугольник преобразовать в эквивалентную звезду, сопротивления которой будут включены последовательно с Z. Просуммировав последовательно включенные сопротивления, получим схему звезда-звезда без нулевого провода, расчет которой рассмотрен выше. По найденным в преобразованной схеме токам определяем напряжения на зажимах треугольника в исходной схеме и затем вычисляем токи а ветвях треугольника.
Иногда целесообразна и обратная эквивалентная замена, как например в схеме рис.4.16. Если несимметричную звезду 2 заменить эквивалентным треугольником, то ветви последнего будут параллельны ветвям треугольника 3. После замены каждой группы параллельных ветвей эквивалентной получим схему рис.4.15, расчет которой мы уже знаем. Заметим, преобразование в схеме рис.4.16 треугольника 3 в эквивалентную звезду не упростило бы задачу, а наоборот усложнило.
Расчет более сложных несимметричных трехфазных цепей и особенно при наличии взаимной индуктивности, которую, как правило целесообразно развязать, производится либо методом контурных токов, либо путем решения уравнений Кирхгофа, не исключается и применение метода узловых потенциалов.
Особые случаи несимметрии трехфазной нагрузки
Под особыми случаями несимметрии понимают такие режимы работы симметричных трехфазных цепей, которые имеют место в аварийных случаях – при обрыве каких-либо ветвей или КЗ каких-либо элементов. В этих аварийных случаях цепь перестает быть симметричной и в принципе её расчет производится ранее рассмотренными методами. Однако при этом появляется ряд важных особенностей, облегчающих расчет, из-за которых мы и рассматриваем данную тему. Разберем ряд примеров.
1. Обрыв линейного провода в схеме звезда-звезда с нулевым проводом (рис.4.17,а). В нормальном режиме работы (рубильник Р включен) токи будут следующими: I A= U A/ Z; I B= U B/ Z; I C= U C/ Z; I N=0. В аварийном режиме (рубильник Р выключен): I A=0; I B= U B/ Z; I C= U C/ Z; I N= I A+ I B. Отсюда следует, что токи I B и I C не изменяются по сравнению с нормальным режимом, появляется ток в нулевом проводе, который по величине равен току I A нормального режима. По этому поводу говорят, что нулевой провод воспринимает на себя ток оборванной фазы. На рис.4.17,б приведена векторная диаграмма рассмотренного аварийного режима при φ>0.
2. Обрыв линейного провода и КЗ фазы в схеме звезда-звезда без нулевого провода (рис.4.18,а). Токи нормального режима (Р1 включен, Р2 выключен) в этой схеме точно такие же как и в схеме рис.4.17,а.
При обрыве линейного провода фазы А (Р1 выключен) I A=0 и поскольку цепь становится несимметричной (Z A=∞, Y A=0), то появляется смещение нейтрали, которое можно вычислить по формуле
Его можно было и не вычислять. Действительно, сопротивления фаз В и С теперь оказываются соединенными последовательно и подключенными к напряжению U BC. Поскольку эти сопротивления одинаковы, то и напряжения на них одинаковы и равны U BC/2. Токи I B=- I C= U BC/2 Z. По сравнению с нормальным режимом работы эти токи уменьшаются и составляют 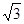/2 от токов нормального режима. Примерный вид векторной диаграммы при φ>0 приведен на рис.4.18,б. Напряжение на обрыве составляет 1.5 от фазного напряжения оборванной фазы, в нашем случае U `A=1.5 U A(см. диаграмму рис.4.18,б).
При КЗ фазы А (Р1 и Р2 включены) Z A=0, Y A=∞ в связи с чем формула для смещения нейтрали дает результат U 010= U A. В его справедливости можно убедиться из схемы поскольку теперь точки 0 и 01 соединяются друг с другом. Напряжения на сопротивлениях фаз В и С оказываются такими (см. диаграмму рис.4.18,в) U ` A=- U AB= U BA U ` B= U CA. Поэтому токи
I B= U BA/ Z; I C= U CA/ Z; I A=-(I B+ I C).
Из этих выражений видно, что величины токов I B и I С на 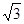больше этих же токов нормального режима, а ток I А, как следует из диаграммы рис.4.18,в, построенной при φ>0, возрастает по сравнению с нормальным режимом в 3 раза.
3. Обрыв линейного провода в схеме звезда-треугольник (рис.4.19,а). В нормальном режиме работы (рубильник Р включен) токи в схеме такие: I AB= U AB/ Z; I BC= U BC/ Z; I CA= U CA/ Z, I л= 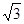I ф.
 |
При обрыве линейного провода фазы А (рубильник Р выключен) I A=0; I BC= U BC/ Z; I AB= I CA=- U BC/2 Z; I B=- I C= I BC- I AB. Из этих выражений вытекает, что по сравнению с нормальным режимом ток I BС не изменяется, величины токов I AB и I СА уменьшаются в 2 раза, а величины токов I B и I С составляют
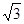/2 от токов нормального режима, в чем можно убедиться из векторной диаграммы рис.4.19,в, построенной при φ>0. Из этой же диаграммы можно определить напряжение на обрыве U `A=1.5 U A.
Измерение активной и реактивной мощностей трехфазной нагрузки
Для симметричных цепей было показано, что активная мощность P = 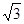U л I лcosφ. В случае несимметричной нагрузки этой формулой пользоваться нельзя. Поскольку несимметричные цепи рассчитываются как правило комплексным методом, то обычно определяют комплексную мощность всей цепи 
а P =Re[ S ], Q =Im[ S ].
Рассмотрим вопрос об измерении мощностей.
 |
Активную мощность в симметричных цепях измеряют с помощью схем с одним ваттметром. Схема рис.4.20,а применяется в случаях, когда имеется нулевой провод, или доступна нулевая точка источника либо приемника. Ваттметр будет показывать мощность одной фазы. Чтобы получить мощность всей цепи, нужно показание ваттметра умножить на 3, т.е. Р =3 N, где N – показание ваттметра. Однако в симметричных цепях нулевой провод обычно не применяют и часто недоступны нулевые точки ни источника ни приемника. Тогда применяют схему с искусственной нулевой точкой (рис.4.20,б). В этой схеме сумма сопротивления обмотки напряжения ваттметра r 1 и должна равняться r. Мощность цепи
Р =3 N.
Активную мощность в несимметричных цепях с нулевым проводом измеряют по схеме трех ваттметров (рис.4.21). В этой схем мощность цепи Р = N 1+ N 2+ N 3.
В цепях без нулевого провода активную мощность измеряют по схеме двух ваттметров (схема Арона), приведенной на рис.4.22,а. Эта схема применяется как при симметричной нагрузке, так и при несимметричной. Ранее указывалось, что система линейных напряжений может быть приписана только двум ЭДС, например таким, которые показаны на рис.4.22,а. Ваттметры измеряют активные мощности этих ЭДС. Согласно балансу мощности точно такую же мощность потребляет нагрузка. Следовательно, мощность цепи Р = N 1+ N 2. Следует иметь в виду, что возможен такой режим работы цепи, когда стрелка одного из ваттметров отклоняется в обратную сторону не смотря на правильное его включение. Тогда, чтобы сделать отсчет по шкале прибора, нужно изменить подключение обмотки напряжения или тока на противоположное. Для этого на ваттметре имеется специальный переключатель (+ и -). Если переключатель находится в положении «-«, то его показание следует считать отрицательным.
Для случая симметричной нагрузки покажем чему равны показания ваттметров и связь этих показаний с углом φ. Первый ваттметр включен на напряжение U AC и по нему протекает ток I A, поэтому его показание
.
Для определения угла между векторами U AC и I A обратимся к векторной диаграмме цепи (рис.4.22,б), из которой видно, что он равен 30˚-φ. Тогда
.
Второй ваттметр включен на напряжение U ВC и по нему протекает ток I В, угол между которыми составляет 30˚+φ (см. диаграмму рис.4.22,б), поэтому
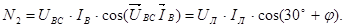
Сумма показаний ваттметров
N 1+ N 2= U л I л[cos(30˚-φ)+cos(30˚+φ)]=2 U л I л cos30˚ cosφ= 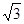U л I л cosφ= P.
Как следует из выражений для N 1 и N 2 показания их одинаковы только при φ=0. При φ=60˚ N 2=0, а при φ>60˚ N 2<0. При φ=-60˚ N 1=0, а при φ<-60˚ N 1<0. При φ=±90˚ N 1=- N 2.
Измерение реактивной мощности имеет большое значение в электроэнергетических установках. В однофазных цепях её измеряют с помощью специальных реактивных ваттметров, схема подключения которых точно такая же как ваттметров активной мощности. Они имеют только конструктивное отличие. В трехфазных цепях реактивную мощность можно измерять как с помощью реактивных ваттметров, так и с помощью ваттметров активной мощности, включенных по специальным схемам. Рассмотрим последний метод.
 |
В симметричных трехфазных цепях реактивную мощность можно измерять одним ваттметром по схеме рис.4.23,а. К ваттметру подведено напряжение U BC и по нему протекает ток I A, поэтому его показание
N = U BC I Acosβ1.
Из векторной диаграммы (рис.4.23,б) имеем β1=90˚-φ, поэтому
N = U л I лcos(90˚-φ)= U л I лsinφ.
Так как Q = 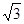U л I лsinφ, то получаем, что Q = 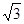N.
Однако даже при незначительной асимметрии схема рис.4.23,а дает большие погрешности. Значительно меньшую погрешность дает схема с двумя ваттметрами (рис.4.24). В этой схеме показание W1 точно такое же, как и в схеме рис.4.23,а, а W2 показывает
N 2= U АВ I Сcosβ2= U л I лcos(90˚-φ)= U л I лsinφ,
Поскольку из диаграммы рис.4.23,б следует, что β2=90˚-φ. Сумма показаний W1 и W2
N 1+ N 2=2 U л I лsinφ.
Следовательно, Q = 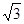(N 1+ N 2/2.
Приведенные схемы измерения реактивной мощности непригодны для несимметричных цепей, в которых Q измеряют с помощью трехфазных реактивных ваттметров.
Вращающееся магнитное поле
Одним из преимуществ трехфазных токов является возможность получения вращающегося магнитного поля, лежащего в основе принципа действия наиболее распространенных двигателей переменного тока. Рассмотрим обмотку. По которой протекает синусоидальный ток в направлении, показанном на рис.4.24. Этот ток будет создавать магнитное поле с магнитной индукцией В, положительное направление которой показано на рис.4.24. Поскольку магнитная индукция пропорционально току, а он изменяется в пределах от I m до - I m, то и индукция будет меняться от В m до - В m. Такое магнитное поле называется пульсирующим и на его основе может быть построен электродвигатель, однако он обладает плохими характеристиками.
Рассмотрим случай, когда обмотка не одна, а три и расположены они под углом 120˚ друг по отношению к другу (рис.4.25,а). Пусть обмотки будут подключены к симметричному трехфазному источнику и их токи будут направлены от начал обмоток к их концам.
 |
Пусть i A= I msin ωt; i B= I msin(ωt- 3π/2); i C= I msin(ωt+ 3π/2). Их графики приведены на рис.4.25,б. Каждый из токов будет создавать магнитное поле с индукциями В 1, В 2 и В 3, положительные направления которых указаны на рис.4.26. Изобразим мгновенные значения индукций В 1, В 2, В 3 и результирующей индукции, создаваемой тремя обмотками для моментов времени ωt=0 (i A=0, i B=-0.867 I m, i C=0.867 I m, рис.4.26,а); ωt=π/2 (i A= I m, i B=-0.5 I m, i C=-0.5 I m, рис.4.26,б); ωt=π (i A=0, i B=0.867 I m, i C=-0.867 I m, рис.4.26,в) и ωt=3π/2 (i A=- I m, i B=0.5 I m, i C=0.5 I m, рис.4.26,г). Видим, что с увеличением времени вектор результирующей магнитной индукции остается по величине и вращается с угловой частотой ω в направлении обмотки с отстающим током. Такое магнитное поле Если отстающий ток пропустить не по второй обмотке, а по третьей, то направление вращения результирующего магнитного поля изменится на противоположное.
Чтобы усилить вращающееся магнитное поле путь его замыкания делают по ферромагнитным материалам.
В схеме рис.4.25,а (одна пара полюсов) за один период переменного тока вектор результирующей магнитной индукции делает один оборот. Поскольку частота вращения магнитного поля обычно задается в оборотах в минуту, то n =60 f/p, где р – число пар полюсов.
Принцип действия асинхронного и синхронного электродвигателей
Наиболее распространенным в промышленности типом двигателя переменного тока являются трехфазный асинхронный двигатель (АД) (рис.4.27). Он состоит из неподвижной части – статора, представляющего собой цилиндр, изготовленный из отдельных листов электротехнической стали. В углублениях статора, называемых пазами и расположенными равномерно по всей его окружности, размещаются обмотки, создающие вращающееся магнитное поле, как рассмотрено выше. Подвижная часть - ротор представляет собой тоже цилиндр, расположенный внутри статора, он также изготовлен из отдельных листов электротехнической стали. В пазах ротора находятся обмотки, которые либо замкнуты накоротко (короткозамкнутый АД), либо на внешнее сопротивление (АД с фазным ротором). Допустим, что вначале ротор неподвижен. Тогда вращающееся магнитное поле, пересекая проводники обмоток ротора, наводит в них ЭДС. Поскольку обмотки ротора замкнуты, то в них возникают токи. Механическое взаимодействие токов ротора с вращающимся магнитным полем приводит к тому, что ротор начинает вращаться в ту же сторону что и магнитное поле статора (в этом можно убедиться по правилу левой руки). В установившемся режиме частота вращения ротора ωр=(0.95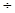 
0.98)ω. Двигатель потому и называется асинхронным, что его ротор вращается несинхронно (асинхронно) с магнитным полем. Причем ωр принципиально не может равняться ω, т.к. в этом случае вращающееся магнитное поле не пересекало бы проводники обмоток ротора, в них не наводились бы ЭДС, не возникали токи и не создавался бы вращающий момент. Если увеличивать нагрузку двигателя, то ротор будет вращаться медленнее, наводимые в обмотках ротора ЭДС и токи увеличатся, а значит возрастет и вращающий момент. Правда возрастание вращающего момента возможно только до определенного предела, называемого критическим, при превышении которого двигатель останавливается (опрокидывается).
Синхронный двигатель отличается от асинхронного только ротором, а именно: по обмоткам ротора пропускают постоянный ток, который создает постоянный же магнитный поток, который «сцепляется» с магнитным полем статора и заставляет ротор вращаться синхронно с вращающимся магнитным полем.
Основы метода симметричных составляющих
Для анализа и расчета несимметричных режимов в трехфазных цепях широко применяется метод симметричных составляющих. Он основан на представлении любой несимметричной системы величин (Е, U, I, Ф и т.д.) в виде суммы трёх систем симметричных величин (рис.4.28). Симметричные системы, образующие в совокупности несимметричную систему, называются симметричными составляющими последней. Симметричные составляющие отличаются друг от друга порядком следования фаз и называются системой прямой, обратной и нулевой последовательностей. Величинам, относящимся к системам прямой, обратной и нулевой последовательностей, принято приписывать индексы 1, 2 и 0 соответственно. Система прямой последовательности имеет такую же последовательность, как и исходная система. Система обратной последовательности имеет противоположную по сравнению с исходной системой последовательность. Система нулевой последовательности состоит из трех одинаковых по величине и направлению векторов. В связи с этим можно записать следующие соотношения: 
Комплексное число 
называется фазным множителем и обозначается как 
Умножение любого вектора на а соответствует повороту его на 120о против часовой стрелки. Учтём, что 
Последнее позволяет исключать а в степени, большей двух. Поскольку 1, а и а 2 образуют симметричную систему, то 1+ а + а 2=0. Используя фазный множитель, можно так переписать взаимосвязь величин, относящихся к разным последовательностям: 
Докажем, что несимметричную систему векторов А, В и С можно разложить на симметричные составляющие. Если это так, то А = А 1+ А 2+ А 0; В = В 1+ В 2+ В 0; С = С 1+ С 2+ С 0. Или А = А 1+ А 2+ А 0; В = а 2 А 1+ а А 2+ А 0; С = а А 1+ а 2 А 2+ А 0. Мы получили три уравнения для трех неизвестных величин, что и доказывает возможность разложения несимметричной системы на симметричные составляющие. Если взять сумму этих уравнений, то получим: А + В + С = (1+ а+а 2) А 1+(1+ а+а 2) А 2+3 А 0, откуда 
Если те же уравнения сложить после умножения второго из них на а, а третьего на а 2, то получим А +а В +а 2 С = (1+ а 3 +а 3) А 1+(1+ а 2 +а 4) А 2+(1+ а+а 2) А 0, откуда 
Аналогично после умножения второго уравнения на а 2, третьего на а и суммирования получим А +а 2 В +а С = (1+ а 4 +а 2) А 1+(1+ а 3 +а 3) А 2+(1+ а+а 2) А 0, откуда 
По формулам для А 1, А 2 и А 3 можно производить как аналитическое, так и графическое разложение несимметричной системы на симметричные составляющие.
Отметим некоторые свойства трехфазных цепей в отношении симметричных составляющих.
1. Ток в нейтральном проводе равен сумме линейных токов. Если последние образуют несимметричную систему и мы их раскладываем на симметричные составляющие, то ток нулевой последовательности будет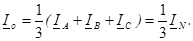 
Таким образом, по нейтральному проводу протекает тройной ток нулевой последовательности. На этом свойстве основана работа фильтров токов нулевой последовательности.