Цель работы – исследование влияния температурного тушения свечения кристаллофосфоров.
Приборы и материалы: источник постоянного тока Б 5-24, источник ультрафиолетового излучения ДРШ 250, светофильтр типа УФС-1, зеркало, образец кристаллофосфора на стеклянной подложке, фотоэлектронный умножитель ФЭУ-27, плитка, медь-константановая термопара, ЛАТР, милливольтметр М 906-2, микроамперметр М 244.
Теоретическая часть
Явление люминесценции. Основу современной оптоэлектроники составляют люминесцентные генераторы оптического излучения. Явление люминесценции известно уже более полувека, однако лишь в последние два десятилетия наблюдалось бурное развитие приборов на ее основе. Существует несколько видов люминесценции, из которых наиболее важными представляются электро - и фотолюминесценция. В первом случае возбуждение атомов вещества происходит под действием электрического поля, а во втором – при поглощении более коротковолнового оптического излучения. Электролюминесценцию можно, в свою очередь, разделить на два вида: катодолюминесценция, которая вызывается свечением люминофора под действием ускоренных в электрическом поле заряженных частиц, и широко применяется в различных типах вакуумных и газоразрядных приборов, и инжекционная люминесценция, происходящая за счет излучения фотонов электронами при изменении их энергетического состояния, вызванного протеканием электрического тока. На ее основе работают такие приборы, как светодиоды и инжекционные лазеры.
Инжекционная люминесценция. При поглощении полупроводником кванта света возможен процесс генерации пары носителей электрон-дырка. Следовательно, в процессе рекомбинации, который противоположен процессу генерации носителей, возможно излучение кванта света. Рекомбинация электронов и дырок в полупроводнике может быть вызвана несколькими конкурирующими процессами, среди которых следует выделить:
– прямые и непрямые переходы зона-зона;
– ловушечные уровни, обусловленные атомами примеси, внутри запрещенной зоны;
– поверхностные дефекты кристаллической решетки.
Все эти процессы могут идти по двум направлениям, как с излучением кванта света, так и без излучения, когда энергии рекомбинации затрачивается на нагрев кристалла. Чтобы определить спектр рекомбинационного излучения, проведем упрощенный анализ этого процесса. Для этого предположим, что при рекомбинации электрона с энергией Е 1 и дырки с энергией Е 2 происходит излучение фотона с энергией Еф = Δ Е = Е 1 – Е 2. Длина волны излучения может быть определена из формулы Планка
λ = hc/ Δ Е, (1)
где h – постоянная Планка, h = 6,626·10-34 Дж·с;
с – скорость света в вакууме, с = 299792458 м/с;
Δ Е – энергия, выделившаяся в результате рекомбинации и равная энергии фотона Еф.
Вероятность рекомбинации будет пропорциональна соответствующим концентрациям электронов и дырок п (Е 1) и р (Е 2), а вероятность излучения фотона с энергией Еф = Δ Е может быть получена путем интегрирования функции концентраций по всем значениям энергий. Общий вид функций распределения разрешенных энергетических состояний электронов и дырок в прямосмещенном р-п- переходе приведен на рис.1. Тогда функцию распределения концентраций носителей можно получить путем перемножения функции разрешенных энергетических состояний и функции Ферми F (Е), которая определяет вероятность заселения состояния с данной энергией. Таким образом,
п (Е 1) = Sc (Е 1) F (Е 1), (2)
и аналогично для дырок
р (Е 2) = Sν (Е 2)(1 – F (Е 2)). (3)
Для простейшей модели предполагается, что заряженные частицы (электроны и дырки) движутся свободно внутри полупроводника, причем их эффективная масса отлична от физической массы электрона и зависит от материала. Величина отношений эффективных масс электронов тп и дырок тр к физической массе электрона т 0 для некоторых полупроводниковых материалов приводятся в табл. 1.
Таблица 1.
Основные свойства полупроводниковых материалов при температуре Т = 298 К
| Материал | Запрещенная зона | Граница фотоэффекта λs, мкм | Эффективная масса | ||
| Энергия Еg, эВ | Тип зоны* | электронов тп/т 0 | дырок тр/т 0 | ||
| Ge | 0,66 | Н | 1,88 | 0,22 | 0,30 |
| Si | 1,11 | Н | 1,15 | 0,97 | 0,50 |
| AlP | 2,45 | Н | 0,52 | - | 0,70 |
| AlAs | 2,16 | Н | 0,57 | 0,15 | 0,79 |
| AlSb | 1,58 | Н | 0,75 | 0,12 | 0,98 |
| GaP | 2,26 | Н | 0,55 | 0,82 | 0,60 |
| GaAs | 1,42 | П | 0,87 | 0,07 | 0,48 |
| GaSb | 0,73 | П | 1,7 | 0,04 | 0,44 |
| InP | 1,35 | П | 0,92 | 0,08 | 0,64 |
| InAs | 0,36 | П | 3,5 | 0,02 | 0,40 |
| InSb | 0,17 | П | 7,3 | 0,014 | 0,40 |
*Н – для непрямозонного материала; П – для прямозонного.
Рис. 1. График функции распределения разрешенных энергетических состояний носителей для чистого GaAs
Функции распределения плотности энергетических состояний в соответствии с этой моделью можно записать в виде
Sc (E 1) = 4 π (2 mn/h 2)3/2(E 1 - Ec)1/2 (4)
и
Sν (E 2) = 4 π (3 mр/h 2)3/2(Eν – E 2)1/2. (5)
Будем в целях упрощения считать, что концентрация носителей падает экспоненциально с ростом энергии от дна зоны проводимости Ес для электронов и с уменьшением энергии от потолка валентной зоны Еν для дырок. Выражения для распределения концентраций можно записать в виде
(6)
и
, (7)
где Кп и Кр – константы, связанные с общей концентрацией свободных носителей;
k – постоянная Больцмана, k = 1,38·10-23 Дж/К.
Вид функций распределения концентраций носителей, описываемых выражениями (6) и (7), показан на рис. 2. Спектральная плотность мощности излучения, как функция энергии фотона, определяется
Ф (Еф = hν) = ∫ п (Е 1) р (Е 2) dЕ 1. (8)
Выражение (8) с учетом выражений (6) и (7) можно переписать
,(9)
где Еф = Е 1 – Е 2;
Еg = Ес - Еν – энергия ширины запрещенной зоны, эВ.
| 
|
| Рис. 2. Распределение концентраций свободных носителей | Рис. 3. Спектр рекомбинационного излучения, соответствующий формуле (9) |
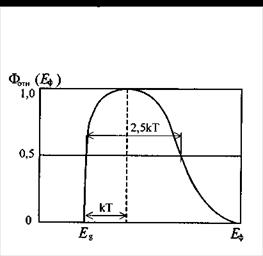
График функции мощности излучения от энергии фотона, или, другими словами, энергетический спектр излучения, изображен на рис. 3. Наибольшая интенсивность излучения наблюдается при энергии фотона Еф = Еg + kT, а полуширина спектра составляет около 2,5 kT. Воспользовавшись данными, приведенными в табл. 1, и с учетом, что при комнатной температуре kT = 0,025 эВ, можно оценить ширину спектральной линии полупроводникового материала по формуле
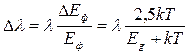. (10)
Реально наблюдаемые спектры светоизлучающих полупроводниковых приборов выглядят более симметрично, и их полуширина находится в пределах от 1,5 kT до 3,5 kT. Наблюдаемое несоответствие с теорией объясняется тем, что высокие концентрации примесей приводят к искажению краев зон в материале, а кроме того, данная модель не учитывает возможность передачи части энергии фонону. Эти эффекты приводят к сдвигу максимума интенсивности излучения в длинноволновую область спектра.
Механизм фотолюминесценции. Внешнее тушение. Спектральный состав свечения люминесценции кристаллов может состоять из одной, двух и более полос. Это означает, что за излучение каждой полосы будут ответственны различные типы центров свечения. Их энергетические уровни в запрещенной зоне располагаются на разной глубине.
Рассмотрим зонную схему кристаллофосфора с двумя типами центров свечения (рис.4). При поглощении кванта энергии основным веществом происходит образование свободного электрона в зоне проводимости и дырки в валентной зоне (переход 1). В дальнейшем, если центры свечения А и В будут находится в ионизованном состоянии (переходы электронов 2 или 4, соответствующие забросу дырок на центры свечения), то рекомбинация с ними свободных электронов (переходы 5 и 6) из зоны проводимости приведет центры свечения (ЦС) в возбужденной состояние с последующим излучением кванта света. В том случае, если один из центров, например, В, является центром тушения (это означает, что рекомбинация ионизованного ЦС с электроном происходит безизлучательно), то произойдет уменьшение энергии излучения люминесценции, называемое внешним тушением, поскольку оно связано с переходами вне ЦС.
Квантовый выход свечения люминесценции может быть записан в виде:
(11)
где wи, wт - вероятности излучательного и безизлучательного переходов.
Роль центров тушения могут играть электронные ловушки. При увеличении концентрации глубоких ЦС, на которых локализуются свободные электроны, увеличивается вероятность перехода 3. Чем выше отношение концентрации центров тушения к концентрации ЦС, тем при более низкой температуре начинается тушение той или иной полосы.
Рассмотренная зонная модель не учитывает колебательного движения
 |
1 – возбуждение в собственной области; 2 – захват дырки ЦС А; 3 – тепловой заброс электрона из валентной зоны на уровень ионизованного ЦС А; 4 – захват дырки ЦС В; 5 – рекомбинация свободного электрона с ЦС А невозможна, т.к. центр А не ионизован.
Рис. 4. Зонная схема кристаллофосфора с двумя типами центров свечения
атомов или ионов, но тем не менее позволяет интерпретировать процессы, связанные с миграцией электронов и дырок на расстояние нескольких постоянных решетки и более. При изучении внутрицентровых процессов колебаниями решетки пренебречь нельзя. В этом случае используется приближение, которое носит название модели потенциальных кривых (рис.5). Эта модель описывает энергетические состояния возбужденного и невозбужденного центров в зависимости от так называемой конфигурационной координаты, которая в случае двухатомной молекулы имеет простой смысл расстояния между ядрами атомов. Переход электронов в возбужденное состояние, как правило, сопровождается изменением сил взаимодействия между атомами, образующими осциллятор. Поэтому положение равновесия потенциальных кривых основного и возбужденного состояний не совпадают. На энергетической диаграмме электронные переходы изображаются стрелками. В возбужденном состоянии система остается некоторое время, достаточное для установления равновесной конфигурации. Релаксация системы из возбужденного состояния в основное сопровождается либо излучением кванта света, либо разменом на фононы. Таким образом, электронный переход может произойти из любой точки потенциальной кривой, в которой колебательная система находится при данной температуре. Вероятность излучательного перехода зависит от вероятности нахождения системы в состоянии соответствия с той или иной координатой (она максимальна для минимума потенциальной кривой).
Внутреннее тушение. При нагревании кристаллофосфора до определенной температуры интенсивность люминесценции начинает резко падать и в том случае, когда это не связано с перехватом энергии возбуждения центрами тушения. Модель потенциальных кривых позволяет объяснить данное явление, получившее название внутреннего тушения, поскольку оно происходит внутри ЦС без связи с кристаллической решеткой основания кристаллофосфора. Вследствие того, что потенциальная кривая возбужденного состояния смещена относительно потенциальной кривой основного состояния и является обычно более пологой, возможно пересечение эти двух кривых (рис.5). Таким образом, находясь в возбужденном состоянии, система будет иметь ту же потенциальную энергию, что и в основном, но при достаточно большей величине колебательной энергии. В этом случае вероятен безизлучательный переход из возбужденного состояния в основное. Избыток энергии передается решетке основания люминофора. Из энергетической диаграммы (рис.5) видно, что энергия активации D e, нужная для того, чтобы вызвать такой безизлучательный переход, равна разности ординат точки, отвечающей нулевому уровню энергии возбужденного состояния, и точки пересечения кривых основного и возбужденного состояний.
Несмотря на существенные различия механизмов внешнего и внутреннего тушения, зависимость интенсивности свечения люминесценции от температуры в обоих случаях описывается уравнением Мотта:
 |
а – потенциальная кривая основного состояния; б – потенциальная кривая возбужденного состояния; 1 – возбуждение; 2 – излучательной процесс
Рис. 5. Модель потенциальных кривых
(12)
где Iл – интенсивность люминесценции при температуре Т;
Iл0 – интенсивность люминесценции при отсутствии тушения;
А – некоторая постоянная, А=twто;
t -среднее время жизни возбужденного ЦС, ч;
wто - вероятность безизлучательного перехода при нулевой температуре;
D e - энергия активации, эВ;
Т - абсолютная температура, К.
В случае внешнего температурного тушения постоянная А характеризует отношение концентрации центров тушения и концентрации центров свечения.
В обоих случаях энергия активации находится по наклону прямой:
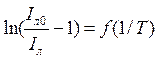. (13)