1. Первая запись массива с ключом р(1) становится корнем дерева.
2. Значение ключа второй записи р(2) сравнивается с р(1), находящимся в корне дерева. Если р(2)<р(1), то вторая запись помещается на левой от корня ветви, в противном случае - на правой ветви. Сейчас получено упорядоченное дерево из первых двух записей, далее на каждом шаге создается упорядоченное дерево из первых i записей.
3. Выбор места i-й записи массива производится следующим образом. Ключ p(i) сравнивается с корневым значением, и выполняется переход по левому адресу (если p(l)>p(i)), а при p(l)<=p(i) - по правому адресу. Ключ достигнутой записи также сравнивается с p(i), и снова организуется переход по левому или правому адресу и т. д. Когда будет достигнут незаполненный адрес связи, то он должен адресовать запись с ключом p(i). Указанные действия повторяются до исчерпания всех записей исходного массива.
Например, упорядоченное дерево на рис. получается из массива записей с ключевыми атрибутами 23, 10, 18, 27, 15,32, 8,30,32,21.
В процессе поиска данных по совпадению в упорядоченном бинарном дереве просматривается некоторый путь по дереву, начинающийся всегда в его корне. Искомое значение ключа q сравнивается со значением корня р(1). Если p(l)>q, просмотр дерева продолжается по левой ветви корня, если p(l)<=q - по правой.
Для произвольной записи дерева с ключом p(i) результаты сравнения означают:
• p(i)=q - запись, удовлетворяющая условию поиска, найдена, и поиск продолжается по правой ветви p(i);
• p(i)>q - производится переход к записи, расположенной на левой ветви p(i);
• p(i)<q - производится переход к записи, расположенной на правой ветви p(i).
Поиск заканчивается, когда у какой-либо записи отсутствует адрес связи, необходимый для дальнейшего продолжения поиска.
Для определения среднего числа сравнений при поиске записи в упорядоченном бинарном дереве рассмотрим ситуацию, когда требуемая запись не найдена, что равноценно вставке записи с искомым значением в дерево. Ненайденный ключ может с одинаковой вероятностью попасть в один из М+1 интервалов, образованных ключами, находящимися в дереве. Неудачный поиск закончится всегда на нулевом адресе связи.
Если обозначить через Е(М) сумму длин всех ветвей дерева с учетом выхода на нулевые адреса связи, то среднее число сравнений при поиске в упорядоченном бинарном дереве С'(М) составит
С'(М)=Е(М)/(М+1).
Дерево с М-1 вершиной отличается от дерева с М вершинами, полученного из него, отсутствием одной концевой записи или (применительно к величине Е) двумя нулевыми адресами связи. Поэтому Е (М) - Е (М -1) =2. Вычислим разность

Математическое ожидание средней длины пути при поиске С'(М) равно сумме математических ожиданий dL от 1 до М. Приближенно заменяя суммирование интегрированием, получаем:
С'(М) = 2ln(М+1).
При замене натурального логарифма на двоичный (ln2 = 0,7) получаем оценку числа сравнений при поиске в упорядоченном бинарном дереве:
C’(M)~2log 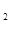 (M+1)
(M+1)
С = 1,4 log М или С ~ log M.
При формировании упорядоченного бинарного дерева в среднем производится
С= l,4M*logM
сравнений пар ключевых атрибутов, где М - число записей, для которых строится дерево.
Включение новой записи при корректировке упорядоченного бинарного дерева означает выполнение одного шага алгоритма формирования дерева с включаемой записью на входе.
Сложность исключения зависит от того, какая запись исключается - концевая, неполная или полная. Первые два случая аналогичны корректировке при списковой организации данных. Адрес связи на исключаемую концевую запись заменяется на признак конца строки, адрес связи на исключаемую неполную запись заменяется на ее собственный адрес связи. При исключении полной записи решается задача о подстановке на ее место другой записи, такой, что ее ключ не нарушает общей упорядоченности бинарного дерева - такие записи называются соседними. Соседняя слева запись - это запись с ключом, который непосредственно меньше ключа данной записи, а ключ соседней справа записи равен или непосредственно больше, чем ключ данной записи.
Способ нахождения соседней справа записи очень простой. Если исключаемая запись имеет ключ q, то от нее происходит переход по правой ветви дерева и производится поиск от достигнутой записи значения q. Запись, на которой остановится поиск, будет соседней. Она пересылается на место исключаемой записи, а сама соседняя запись исключается. Это уже простая задача, так как соседняя запись не может быть полной.
При поиске соседней слева записи надо выполнить переход по левой ветви от данной записи (с ключом q), а дальнейшие действия такие же, как и для поиска соседней справа записи.
| Критерии оценки | Методы организации данных | Лучший метод | ||
| последовательный | цепной | Бинарное дерево | ||
| Время формирования | Mlog 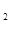 M M
| Mlog 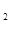 M M
| Mlog 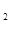 M M
| Исходя из цели проектирования БД |
| Время поиска | log 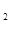 M M
| M | log 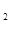 M M
| Последовательный массив, бинарное дерево |
| Время корректировки | M | M | log 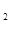 M M
| Бинарное дерево |
| Объем дополнительной памяти | M | M | последовательный |
Это объясняется необходимостью пересылки записей в процессе сортировки последовательного массива, а в цепном каталоге и бинарном дереве при формировании пересылаются адреса связи, а не целые записи.