Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М, находящихся на расстоянии r одна от другой, равна
. (11)
где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞.
Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M e – масса Земли, R e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.
При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h «R e) равна
,
где 
– модуль ускорения свободного падения вблизи поверхности Земли.
13. Чему равен импульс тела, и как можно его изменить?
Векторную величину Ft, равную произведению силы на время ее действия, называют импульсом силы. Векторную величину р=mv, равную произведению массы тела на его скорость, называют импульсом тела.
В СИ за единицу импульса принят импульс тела массой 1 кг, движущегося со скоростью 1 м/с, т.е. единицей импульса является килограмм/метр в секунду (1 кг·м/с).
Изменение импульса тела Dp за время t равно импульсу силы Ft, действующей на тело в течение этого времени.
Группу тел, взаимодействующих не только между собой, но и с телами, не входящими в состав этой группы, называют незамкнутой системой. Силы, с которыми на тела данной системы действуют тела, не входящие в эту систему, называют внешними (обычно внешние силы обозначают буквой F).
Рассмотрим взаимодействие двух тел в незамкнутой системе. Изменение импульсов данных тел происходит как под действием внутренних сил, так и под действием внешних сил.
Согласно второму закону Ньютона, изменения импульсов рассматриваемых тел у первого и второго тел составляют
Dр1=f1t+F1t (3.5)
Dр2=f2t+F2t (3.6)
где t - время действия внешних и внутренних сил.
Почленно сложив выражения (3.5) и (3.6), найдем, что
D(p1+p2)=(f1+f2)t +(F1+F2)t
В этой формуле р=р1+р2 - полный импульс системы, f1+f2=0 (так как по третьему закону Ньютона (f1=-f2), F1+F2=F - равнодействующая всех внешних сил, действующих на тела данной системы. С учетом сказанного формула принимает вид Dр=Ft.
14. Момент инерции и энергия вращения тела. Движение конечностей тела человека.
Моменты инерции симметричных тел.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:
Если тело вращается вокруг неподвижной оси с угловой скоростью 
, то линейная скорость i-ой точки равна 
, где 
, - расстояние от этой точки до оси вращения. Следовательно.
| (5.11) |
где 
- момент инерции тела относительно оси вращения.
В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости 
центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду
| (5.12) |
где 
- момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные кинематические характеристики вращательного движения тела — его угловая скорость (
) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:
и кинетическая энергия
где Iz — момент инерции тела относительно оси вращения.
Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением
где ω1, ω2, и ω3 — главные компоненты угловой скорости.
В общем случае, энергия при вращении с угловой скоростью 
находится по формуле:
, где 
— тензор инерции.
Биомеханика человека
Движения частей тела человека представляют собою перемещения в пространстве и времени, которые выполняются во многих суставах одновременно и последовательно. Движения в суставах по своей форме и характеру очень разнообразны, они зависят от действия множества приложенных сил. Все движения закономерно объединены в целостные организованные действия, которыми человек управляет при помощи мышц. Учитывая сложность движений человека, в биомеханике исследуют и механическую, и биологическую их стороны, причем обязательно в тесной взаимосвязи.
Элементы статики и динамики тела человека
Вертикальное положение тела человека в пространстве, перемещение его по поверхности, различные виды движений (ходьба, бег, прыжки) сложились в процессе длительной эволюции вместе со становлением человека как вида. В процессе антропогенеза, в связи с переходом предков человека к наземным условиям существования, а затем и к перемещению на двух нижних конечностях (задних) весь организм, отдельные его части, органы, включая и опорно-двигательный аппарат, претерпели чрезвычайно сложные изменения.
Прямохождение - первооснова главных приспособительных изменений антропогенеза - освободило верхнюю конечность от опорно-двигательной функции. Верхняя конечность превратилась в орган труда - руку, она могла совершенствоваться в дальнейшем в ловкости движений. Рука, таким образом, является не только органом труда, она также и продукт его. Эти изменения как результат качественно новой функции отразились на строении всех составных частей пояса и свободной части верхней конечности. Плечевой пояс служит не только опорой свободной верхней конечности. Он также значительно увеличивает ее подвижность. Благодаря тому, что лопатка соединяется со скелетом туловища главным образом при помощи мышц, она приобретает большую свободу движений. Лопатка участвует во всех движениях, которые совершает ключица. Кроме того, лопатка может свободно перемещаться независимо от ключицы. В многоосном шаровидном плечевом суставе, который почти со всех сторон окружен мышцами, анатомические особенности строения позволяют производить движения по большим дугам во всех плоскостях. Особенно заметно отразилась специализация функции на строении кисти. Благодаря развитию длинных, очень подвижных пальцев, в первую очередь большого пальца, который противопоставляется остальным, кисть превратилась в сложный орган, выполняющий тонкие, дифференцированные действия.
Нижняя конечность, приняв на себя всю тяжесть тела, приспособилась исключительно к опорно-двигательной деятельности. Вертикальное положение тела в пространстве, Прямохождение отразились на строении и функциях и пояса (таза), и свободной части нижней конечности. Пояс нижней конечности (тазовый пояс) как прочная арочная конструкция, приспособился к передаче тяжести туловища, головы, верхних конечностей на головки бедренных костей. Установившийся в процессе антропогенеза наклон таза в 45-65° способствует перенесению на свободные нижние конечности тяжести тела в наиболее благоприятных для вертикального положения тела биомеханических условиях. Стопа приобрела сводчатое строение, что увеличило ее прочность противостоять тяжести тела и выполнять роль гибкого рычага в перемещении тела. Сильно развилась мускулатура нижней конечности, которая приспособилась к выполнению статических и динамических нагрузок. По сравнению с верхней конечностью мышцы нижней конечности имеют большую массу, в них значительно больше плотной соединительной ткани.
Важным механическим моментом является то, что на нижней конечности мышцы имеют обширные поверхности опоры и приложения силы, прикрепляются сравнительно далеко от точки опоры рычага, на который действуют, но ближе к точке сопротивления. Неодинаковы также отношения групп мышц друг к другу на верхней и нижней конечностях: масса разгибателей нижней конечности относится к массе сгибателей как 3:1, а на верхней конечности это отношение выражается как 1:1,042. На нижней конечности больше развиты разгибатели, чем сгибатели. Это связано с тем, что разгибатели играют большую роль в удержании тела в вертикальном положении и при передвижении в пространстве (ходьба, бег).
На руке сгибатели плеча, предплечья и кисти сосредоточены на передней стороне, поскольку работа, производимая руками, совершается впереди туловища. Хватательные движения производятся кистью также с участием сгибателей. Сравнение поворачивающих мышц (пронаторы, супинаторы) верхней и нижней конечностей, их отношение к остальным мышцам данной конечности также свидетельствуют о том, что на верхней конечности они развиты намного больше, чем на нижней. Масса пронаторов и супинаторов руки относится к остальным мышцам верхней конечности как 1:4,8. На нижней конечности отношение массы поворачивающих мышц к остальным 1:29,3.
Фасции, апоневрозы на нижней конечности в связи с большим проявлением силы при статических и динамических нагрузках развиты значительно больше, чем на верхней конечности. На нижней конечности имеются дополнительные механизмы, которые способствуют удержанию тела в вертикальном положении и обеспечивают передвижение его в пространстве. Наряду с тем что пояс нижней конечности почти неподвижно соединен с крестцом и представляет естественную опору туловища, тенденции таза опрокинуться кзади на головках бедренных костей препятствует сильно развитая подвздошно-бедренная связка тазобедренного сустава. В разогнутом коленном суставе в поперечном направлении образуется ломаная линия вследствие изменения формы латерального и медиального менисков.
На уровне голеностопного сустава при стоянии увеличивается площадь соприкосновения между суставными поверхностями костей голени и таранной кости, так как медиальная и латеральная лодыжки охватывают передний, более широкий отдел блока таранной кости. Фронтальные оси голеностопных суставов устанавливаются друг к другу под углом, открытым кзади. Вместе с тем вертикаль тяжести тела обходит голеностопный сустав спереди, приводя как бы к ущемлению переднего, более широкого отрезка блока таранной кости между медиальной и латеральной лодыжками. Суставы верхней конечности (плечевой, локтевой, лучезапястный) таких тормозных механизмов не имеют. Глубоким изменениям в процессе антропогенеза подверглись кости, мышцы туловища, особенно осевого скелета позвоночного столба, который является опорой для головы, верхних конечностей, органов грудной и брюшной полостей. В связи с прямохождением образовались изгибы позвоночника, развилась мощная дорсальная мускулатура. Кроме того, позвоночник практически неподвижно соединен в парном прочном крестцово-подвздошном сочленении с поясом нижних конечностей (с тазовым поясом), который в биомеханическом отношении служит распределителем тяжести туловища на головки бедренных костей. Наряду с изложенными анатомическими факторами - особенностями строения нижней конечности, туловища, выработанными в процессе антропогенеза для поддержания тела в вертикальном положении, обеспечения устойчивого равновесия и динамики, особое внимание должно быть уделено положению центра тяжести тела.
В живом организме положение центра тяжести изменяется в зависимости от перемещения подвижных его частей (движения конечностей, изменение положения головы, наклоны туловища, перемещение внутренних органов и др.).
Центр тяжести тела человека находится на уровне II крестцового позвонка; отвесная линия центра тяжести проходит на 5 см позади поперечной оси тазобедренных суставов (приблизительно на 2,6 см кзади от большого вертела) и на 3 см впереди от поперечной оси голеностопного сустава. Центр тяжести головы располагается немного кпереди от поперечной оси атлантозатылочного сустава. Общий центр тяжести головы и туловища находится на уровне середины переднего края Х грудного позвонка.
С целью сохранения устойчивого равновесия тела человека на плоскости необходимо, чтобы перпендикуляр, опущенный из центра тяжести, падал на площадь, занимаемую обеими ступнями. Тело стоит тем прочнее, чем шире площадь опоры и чем ниже расположен центр тяжести. Поэтому для всех случаев вертикального положения тела человека сохранение равновесия является главной задачей, так как в противном случае должно последовать падение. Однако, напрягая соответствующие мыщцы, мы можем удержать тело в различных положениях (в известных пределах) даже тогда, когда проекция центра тяжести выведена за пределы площади опоры (сильный наклон туловища вперед, в стороны и т.д.). Вместе с тем стояние и передвижение человеческого тела нельзя считать устойчивым, при относительно длинных ногах человек имеет сравнительно небольшую площадь опоры. Поскольку центр тяжести тела человека расположен относительно высоко (на уровне II крестцового позвонка), а опорная площадь (площадь двух подошв и пространства между ними) незначительна, устойчивость тела очень невелика. Поэтому удержание тела в состоянии равновесия силой мышечных сокращений предотвращает его падение, и части тела (голова, туловище, конечности) удерживаются в надлежащем соотношении для каждого положения тела. Например, если при стоянии будет нарушено соотношение частей тела (вытягивание вперед рук, сгибание позвоночника и т.д.), то соответственно изменяются положение и равновесие других частей тела. Статистические и динамические моменты действия мускулатуры находятся в прямой связи с состоянием положения центра тяжести тела. Поскольку центр тяжести всего тела располагается на уровне II крестцового позвонка позади поперечной линии, соединяющей центры тазобедренных суставов, тенденции туловища (вместе с тазом.) опрокинуться назад противостоят сильно развитые мышцы и связки, укрепляющие тазобедренные суставы. Так обеспечивается равновесие всей верхней части тела, покоящейся на ногах в вертикальном положении.
Тенденция тела упасть вперед при стоянии связана также с прохождением вертикали центра тяжести впереди (на 3-4 см) от поперечной оси голеностопных суставов. Падению противостоят действия мышц задней поверхности голени. Если отвесная линия центра тяжести переместится еще дальше кпереди к пальцам, то сокращением задних мышц голени пятка приподнимается, отрывается от плоскости опоры и тогда отвесная линия центра тяжести перемещается вперед и опорой служат пальцы стопы:
Кроме опорной, нижние конечности выполняют локомоторную функцию, перемещая тело в пространстве. Например, при ходьбе тело человека совершает поступательное движение, попеременно опираясь то на одну, то на другую ногу; последние поочередно совершают маятникообразные движения. При ходьбе одна из нижних конечностей в определенный момент является опорной (задняя), другая-свободной (передняя). При каждом новом шаге свободная нога становится опорной, а опорная выносится вперед и делается свободной.
Сокращения мышц нижней конечности при ходьбе заметно усиливают изогнутость подошвы стопы, увеличивают кривизну ее поперечного и продольного сводов. В этот же момент туловище несколько наклоняется вперед вместе с тазом на головках бедренных костей. Если первый шаг начат правой ногой, то правая пятка, затем середина подошвы и пальцы поднимаются над плоскостью опоры, правая нога сгибается в тазобедренном и коленном суставах и выносится вперед. Одновременно тазобедренный сустав этой стороны и туловище следуют вперед за свободной ногой. Эта (правая) нога энергичным сокращением четырехглавой мышцы бедра выпрямляется в коленном суставе, касается поверхности опоры и становится опорной. В этот момент другая (левая) нога (до начала момента задняя, или опорная) отрывается от плоскости опоры, выносится вперед, становясь передней, свободной ногой. Правая нога в это время остается позади в качестве опорной. Вместе с нижней конечностью передвигается и тело вперед и несколько вверх. Так обе конечности поочередно проделывают одни и те же движения в строго определенной последовательности, подпирая тело то с одной стороны, то с другой и толкая его вперед. Однако во время ходьбы не бывает момента, чтобы обе ноги были одновременно оторваны от поверхности земли (плоскости опоры). Передняя (свободная) конечность успевает всегда коснуться плоскости опоры пяткой раньше, чем задняя (опорная) нога полностью отделится от нее. Этим ходьба отличается от бега и прыжков. Вместе с тем при ходьбе существует момент, когда обе ноги одновременно касаются земли, причем опорная всей подошвой, а свободная пальцами, перед тем как последние отделятся от земли. Чем быстрее ходьба, тем короче момент одновременного прикосновения обеих ног к плоскости опоры.
Прослеживая при ходьбе изменения положения центра тяжести, можно отметить движение всего тела вперед, вверх и в стороны в горизонтальной, фронтальной и сагиттальной плоскостях. Наибольшее смещение вперед происходит в горизонтальной плоскости. Смещение вверх и вниз составляет 3-4 см, а в стороны (боковые качания) - на 1-2 см. Характер и степень этих смещений подвержены значительным колебаниям и зависят от возраста, пола и индивидуальных особенностей. Совокупность этих факторов определяет индивидуальность походки, хотя последняя не есть нечто постоянное, так как может изменяться под влиянием тренировки. В среднем длина обычного спокойного шага 66 см и по времени занимает 0,6 с.
При ускорении ходьбы момент одновременного касания почвы обеими ногами выпадает, шаг переходит в бег. Поэтому бег отличается от ходьбы тем, что при нем имеют место только попеременная опора и касание площади опоры то одной, то другой ногой.
Момент инерции.
Моментом инерции материальной точки массы m относительно осиназывается величина, равная:
I = m·r2, где r - кратчайшее расстояние от оси вращения до точки.
Момент инерции твердого тела равен сумме моментов инерции его частей:
I = Smi·ri2
Следовательно, момент инерции твердого тела зависит от:
- массы тела;
- формы и размеров тела;
- распределения массы относительно оси вращения (при переносе оси вращения или отдельных частей тела его момент инерции изменяется).
Для симметричных тел момент инерции рассчитывается с помощью интегрального исчисления.
15. Момент силы. Рычаги. Виды рычагов в опорно-двигательном аппарате человека.
Момент силы - векторная величина. Для нахождения ее направления вектора r и F необходимо изобразить исходящими из одной точки и связать с ними правый винт. Затем головку правого винта нужно вращать от r к F. Направление движения винта будет совпадать с вектором M.
Величина вектора момента сил равна:
M = r·F·sin(α) = F·R,
где R = r·sin(α) - плечо силы, равное кратчайшему расстоянию между осью вращения и линией действия силы.
Рыча́г — простейшее механическое устройство, представляющее собой твёрдое тело (перекладину), вращающееся вокруг точки опоры. Стороны перекладины по бокам от точки опоры называются плечами рычага.
Рычаг используется для получения большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие.
Принцип работы рычага является прямым следствием закона сохранения энергии.
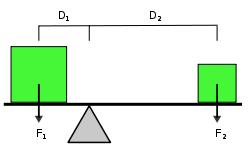Чтобы переместить рычаг на расстояние 
сила, действующая со стороны груза, должна совершить работу равную: 
Если посмотреть с другой стороны, сила, приложенная с другой стороны, должна совершать работу 
где 
— это перемещение конца рычага, к которому приложена сила 
. Чтобы выполнялся закон сохранения энергии для замкнутой системы, работа действующей и противодействующей сил должны быть равны, то есть: 
Различают:
1) рычаги 1 рода, в которых точка опоры располагается между точками приложения сил (детские качели (перекладина), ножницы);
2) рычаги 2 рода, в которых точки приложения сил располагаются по одну сторону от опоры (точка опоры - колесо), приподнимание предмета ломом движением вверх, тачка;
Среди рычагов 2 рода выделяют рычаги 3 рода, с точкой приложения "входящей" силы ближе к точке опоры, чем нагрузки, что даёт выигрыш в скорости и пути задняя дверь или капот легковых автомобилей на газовых пружинах, подъём кузова самосвала (с гидроцилиндром в центре), движение мышцами рук и ног человека и животных.
Костные рычаги – звенья тела, подвижно соединённые в суставах под действием приложенных сил, могут либо сохранять своё положение, либо изменять его. Они служат для передачи движения и работы на расстояние.
Когда силы приложены по обе стороны от оси (точки опоры) рычага, его называют двуплечим, а когда по одну сторону – одноплечим. Для разных мышц, прикреплённых в разных местах костного звена, рычаг может быть разного рода. В природе существуют три рода рычагов: рычаги I-го («весы»), II-го(«тачка») и III-го(«подъемный кран») родов.
Каждый рычаг имеет следующие элементы:
– точку опоры (ось вращения, точка 0);
– как минимум две силы (f и F);
– точки приложения этих сил (А и В);
– плечи рычага (расстояния от точки опоры до точек приложения сил – АО и ВО);
– плечи сил (наикратчайшие расстояния от точки опоры до линий действий сил – опущенные на неё перпендикуляры АО и 0В).
Мерой действия силы на рычаг служит её момент относительно точки опоры – вращательный момент. Момент силы определяется произведением силы на плечо этой силы.
Mf = F * OВ
Mf= F * АО
Момент силы – это векторная величина. Если сила лежит не в плоскости, перпендикулярной оси, то находят составляющую силы, лежащую в этой плоскости. Она и вызывает момент силы относительно оси. Остальные составляющие на момент силы не влияют.
Когда противоположные относительно оси сустава моменты сил равны, звено либо сохраняет своё положение, либо продолжает движение с постоянной скоростью (моменты сил уравновешены). Если же один из моментов сил больше другого, звено получает ускорение в направлении его действия.
В опорно-двигательном аппарате присутствуют рычаги всех трёх родов, причём значительно больше рычагов III-го рода, рычагов скорости, так как мышцы крепятся в основном вблизи суставов.
Таким образом, двигательный аппарат человека по природе своей в большей степени быстрый и ловкий, чем сильный. Кроме этого, во всех костных рычагах имеются потери в силе ввиду того, что мышцы крепятся к костям под острым или тупым углом.
Движущиеся части механизмов обычно бывают соединены частями. Подвижное соединение нескольких звеньев образует кинематическую связь. Тело человека – пример кинематической связи. Опорно-двигательная система человека, состоящая из сочлененных между собой костей скелета и мышц, представляет с точки зрения физики совокупность рычагов, удерживаемых человеком в равновесии. В анатомии различают рычаги силы, в которых происходит выигрыш в силе, но проигрыш в перемещении, и рычаги скорости, в которых, проигрывая в силе, выигрывают в скорости перемещения. Хорошим примером рычага скорости является нижняя челюсть. Действующая сила осуществляется жевательной мышцей. Противодействующая сила – сопротивление раздавливаемой пищи – действует на зубы. Плечо действующей силы значительно короче, чем у сил противодействия, поэтому жевательная мышца короткая и сильная. Когда надо разгрызть что-либо зубами, уменьшается плечо силы сопротивления.
Если рассматривать скелет как совокупность отдельных звеньев, соединенных в один организм, то окажется, что все эти звенья при нормальной стойке образуют систему, находящуюся в крайне неустойчивом равновесии. Так, опора туловища представлена шаровыми поверхностями тазобедренного сочленения. Центр массы туловища расположен выше опоры, что при шаровой опоре создает неустойчивое равновесие. То же относится и к коленному соединению, и к голеностопному. Все эти звенья находятся в состоянии неустойчивого равновесия.
Центр массы тела человека при нормальной стойке расположен как раз на одной вертикали с центрами тазобедренного, коленного и голеностопного сочленений ноги, на 2–2,5 см ниже мыса крестца и на 4–5 см выше тазобедренной оси. Таким образом, это самое неустойчивое состояние нагроможденных звеньев скелета. И если вся система держится в равновесии, то только благодаря постоянному напряжению поддерживающих мышц.
Механическая работа, которую способен совершить человек в течение дня, зависит от многих факторов, поэтому трудно указать какую-либо предельную величину. Это относится и к мощности. Так, при кратковременных усилиях человек может развивать мощность порядка нескольких киловатт. Если спортсмен массой 70 кг подпрыгивает с места так, что его центр массы поднимается на 1 м по отношению к нормальной стойке, а фаза отталкивания длится 0,2 с, то он развивает мощность около 3,5 кВт. При ходьбе человек совершает работу, так как при этом энергия затрачивается на периодическое небольшое поднятие конечностей, главным образом ног.
Работа обращается в нуль, если перемещения нет. Поэтому, когда груз находится на опоре или подставке или подвешен на шест, сила тяжести не совершает работы. Однако, если держать неподвижно на вытянутой руке гирю или гантель, отмечается усталость мышц руки и плеча. Точно так же устают мышцы спины и поясничной области, если сидящему человеку поместить на спину груз.
16. Уравнение моментов для вращательного движения (II закон Ньютона).
Конечно, положение одной, даже «особой», точки далеко не полностью описывает движение всей рассматриваемой системы тел, но все-таки лучше знать положение хотя бы одной точки, чем не знать ничего. Тем не менее рассмотрим применение законов Ньютона к описанию вращения твердого тела вокруг фиксированной оси1.
Начнем с простейшего случая: пусть материальная точка массы m прикреплена с помощью невесомого жесткого стержня длиной r к неподвижной оси ОО/.
Материальная точка может двигаться вокруг оси, оставаясь от нее на постоянном расстоянии, следовательно, ее траектория будет являться окружностью с центром на оси вращения.
Безусловно, движение точки подчиняется уравнению второго закона Ньютона
Однако непосредственное применение этого уравнения не оправдано: во-первых, точка обладает одной степенью свободы, поэтому в качестве единственной координаты удобно использовать угол поворота, а не две декартовые координаты; во-вторых, на рассматриваемую систему действуют силы реакции в оси вращения, а непосредственно на материальную точку − сила натяжения стержня. Нахождение этих сил представляет собой отдельную проблему, решение которой излишне для описания вращения. Поэтому имеет смысл получить на основании законов Ньютона специальное уравнение, непосредственно описывающее вращательное движение.
Пусть в некоторый момент времени на материальную точку действует некоторая сила F, лежащая в плоскости, перпендикулярной оси вращения (рис. 107).
рис. 107
При кинематическом описании криволинейного движения вектор полного ускорения а удобно разложить на две составляющие − нормальную аn, направленную к оси вращения, и тангенциальную аτ, направленную параллельно вектору скорости. Значение нормального ускорения для определения закона движения нам не нужно. Конечно, это ускорение также обусловлено действующими силами, одна из которых − неизвестная сила натяжения стержня.
Запишем уравнение второго закона в проекции на тангенциальное направление:
Заметим, что сила реакции стержня не входит в это уравнение, так как она направлена вдоль стержня и перпендикулярна выбранной проекции. Изменение угла поворота φ непосредственно определяется угловой скоростью
ω = Δφ/Δt,
изменение которой, в свою очередь, описывается угловым ускорением
ε = Δω/Δt.
Угловое ускорение связано с тангенциальной составляющей ускорения соотношением
аτ = rε.
Если подставим это выражение в уравнение (1), то получим уравнение, пригодное для определения углового ускорения. Удобно ввести новую физическую величину, определяющую взаимодействие тел при их повороте. Для этого умножим обе части уравнения (1) на r:
mr2ε = Fτr. (2)
Рассмотрим выражение в его правой части Fτr, имеющее смысл
произведения тангенциальной составляющей силы на расстояние от оси вращения до точки приложения силы. Это же произведение можно представить в несколько иной форме (рис. 108):
рис. 108
M = Fτr = Frcosα = Fd,
здесь d − расстояние от оси вращения до линии действия силы, которое также называют плечом силы.
Эта физическая величина − произведение модуля силы на расстояние от линии действия силы до оси вращения (плечо силы) М = Fd − называется моментом силы. Действие силы может приводить к вращению как по часовой стрелке, так и против часовой стрелки. В соответствии с выбранным положительным направлением вращения следует определять и знак момента силы. Заметьте, что момент силы определяется той составляющей силы, которая перпендикулярна радиус-вектору точки приложения. Составляющая вектора силы, направленная вдоль отрезка, соединяющего точку приложения и ось вращения, не приводит к раскручиванию тела. Эта составляющая при закрепленной оси компенсируется силой реакции в оси, поэтому не влияет на вращение тела.
Запишем еще одно полезное выражения для момента силы. Пусть сила F приложена к точке А, декартовые координаты которой равны х, у (рис. 109).
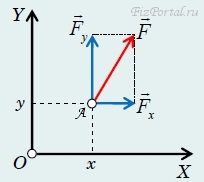
рис. 109
Разложим силу F на две составляющие Fх, Fу, параллельные соответствующим осям координат. Момент силы F относительно оси, проходящей через начало координат, очевидно равен сумме моментов составляющих Fх, Fу, то есть
М = хFу − уFх.
Аналогично, тому, как нами было введено понятие вектора угловой скорости, можно определить также и понятие вектора момента силы. Модуль этого вектора соответствует данному выше определению, направлен же он перпендикулярно плоскости, содержащей вектор силы и отрезок, соединяющий точку приложения силы с осью вращения (рис. 110).
рис. 110
Вектор момента силы также может быть определен как векторное произведение радиус-вектора точки приложения силы на вектор силы
Заметим, что при смещении точки приложения силы вдоль линии ее действия момент силы не изменяется.
Обозначим произведение массы материальной точки на квадрат расстояния до оси вращения
mr2 = I
(эта величина называется моментом инерции материальной точки относительно оси). С использованием этих обозначений уравнение (2) приобретает вид, формально совпадающий с уравнением второго закона Ньютона для поступательного движения:
Iε = M. (3)
Это уравнение называется основным уравнением динамики вращательного движения. Итак, момент силы во вращательном движении играет такую же роль, как и сила в поступательном движении, − именно он определяет изменение угловой скорости. Оказывается (и это подтверждает наш повседневный опыт), влияние силы на скорость вращения определяет не только величина силы, но и точка его приложения. Момент инерции определяет инерционные свойства тела по отношению к вращению (говоря простым языком − показывает, легко ли раскрутить тело): чем дальше от оси вращения находится материальная точка, тем труднее привести ее во вращение.
Уравнение (3) допускает обобщение на случай вращения произвольного тела. При вращении тела вокруг фиксированной оси угловые ускорения всех точек тела одинаковы. Поэтому аналогично тому, как мы проделали при выводе уравнения Ньютона для поступательного движения тела, можно записать уравнения (3) для всех точек вращающегося тела и затем их просуммировать. В результате мы получим уравнение, внешне совпадающее с (3), в котором I − момент инерции всего тела, равный сумме моментов составляющих его материальных точек, M − сумма моментов внешних сил, действующих на тело.
Покажем, каким образом вычисляется момент инерции тела. Важно подчеркнуть, что момент инерции тела зависит не только от массы, формы и размеров тела, но и от положения и ориентации оси вращения. Формально процедура расчета сводится к разбиению тела на малые части, которые можно считать материальными точками (рис. 111),
рис. 111
и суммированию моментов инерции этих материальных точек, которые равны