Глава 19. Касательная.
А.
№У19.1) Прямая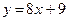 
параллельна касательной к графику функции 
. Найдите абсциссу точки касания.
№У19.2) Угловой коэффициент касательной к графику функции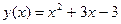 
равен значению функции в точке касания. Найдите сумму абсцисс точек касания.
Ответы к главе 19. №19.1) 1,5; №19.2) -1.
Глава 20. Исследование и графики функций.
А.
№У20.1) Построить график функции: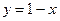 
.
№20.2) Построить график функции: 
.
№20.3) Построить график функции: 
.
№20.4) Построить график функции: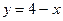 
.
№С20.5) Построить график функции: 
.
№20.6) Построить график функции: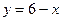 
.
№20.7) Построить график функции: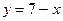 
.
№20.8) Построить график функции: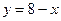 
.
№20.9) Построить график функции: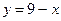 
.
№20.10) Построить график функции: 
.
№20.11) Найти область определения функции: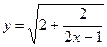 
.
№20.12) Найти область определения функции: 
.
№20.13) Найти область определения функции: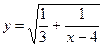 
.
№У20.14) Найти область определения функции: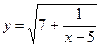 
.
№20.15) Найти область определения функции: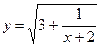 
.
№С20.16) Найти область определения функции: 
.
№У20.17) Найдите область определения дроби 
.
№У20.18) Найдите нули функции 
.
№У20.19) Найти область определения функции 
.
№У20.20) Найти область определения функции 
№У20.21) Найдите область определения функции 
.
№У20.22) Найти область значений функции: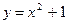 
.
№У20.23) Найти область определения функции: 
.
Ответы к главе 20. №20.11)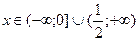 
; №20.12) 
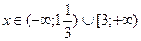; №20.13) 
; №20.14)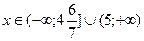 
; №20.15) 
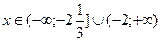; №20.16) 
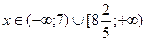; №20.17) 
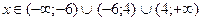; №20.18) 
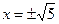; №20.19) 
; №20.20)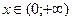 
; №20.21) 
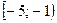; №20.22) 
; №20.23)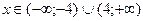 
.
В.
№У20.24) Кривая, изображенная на рисунке, может быть графиком функции…
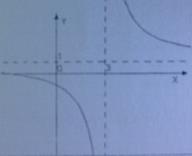
№У20.25) Постройте на плоскости и выделите штриховкой область, заданную системой неравенств 
.
№С20.25.1) Постройте на плоскости и выделите штриховкой область, заданную системой неравенств 
.
№У20.26) Постройте на плоскости и выделите штриховкой область, заданную системой неравенств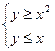 
.
№С20.27) Постройте на плоскости и выделите штриховкой область, заданную системой неравенств 
.
Ответы к главе 20. №20.24)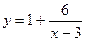 
.
Глава 32. Вписанные и описанные окружности.
А.
№У32.1) Найдите (в см) длину дуги окружности, ограничивающей круг площадью 
, если угловая мера этой дуги равна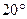 
.
№С32.2) Радиусы двух кругов относятся как 1:2. Найти площадь меньшего круга, если длина окружности большего круга равна 
.
№У32.3) Площади двух кругов относятся как 1:16. Радиус меньшего равен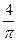 
. Найдите длину большей окружности.
№С32.3.1) Площади двух кругов относятся как 2:18. Радиус меньшего равен 
. Найдите длину большей окружности.
№У32.4) Длины двух окружностей относятся как 2:10. Радиус меньшего круга равен 
. Найдите площадь большего круга.
№С32.5) Длины двух окружностей относятся как 3:18. Радиус меньшего круга равен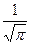 
. Найдите площадь большего круга.
№С32.6) Около треугольника, стороны которого равны 6 см, 8 см и 10 см, описана окружность. Найдите ее радиус.
№С32.7) В треугольник, стороны которого равны 3см, 4см и 5см, вписана окружность. Найдите ее радиус.
№У32.8) В прямоугольный треугольник, катеты которого равны 6 см и 8 см, вписана окружность. Найдите ее радиус.
Ответы к главе 32.
№32.1)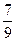 
; №32.2) 
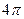; №32.3) 32; №32.3.1) 42; №32.4) 100; №32.5) 36; №32.6) 5 см; №32.7) 1 см; №32.8) 2 см.
В.
№У32.9) Две окружности радиусов 
имеют общую хорду длиной 8. Найдите расстояние между центрами окружностей.
№У32.10) В равнобедренную трапецию с основаниями 3см и 5см можно вписать окружность. Найти площадь этой трапеции.
Ответы к главе 32.
№32.9) 1; №32.10)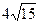 
;
С.
№У32.11) Медиана, проведенная из вершины А треугольника АВС, продлена до пересечения в точке F с описанной окружностью. Найдите сторону АС, если AF=26, BF=10, медиана равна 18.
№У32.12) Вокруг остроугольного равнобедренного треугольника АВС с основанием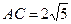 
, описана окружность радиуса 3. Найти длину стороны квадрата, две вершины которого лежат на отрезке 
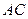, а две оставшиеся вершины на дуге 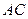окружности, не содержащей точку 
.
№У32.13) В окружность радиуса 25 вписана трапеция с боковой стороной 30 и площадью 1080. Найти основания трапеции.
№У32.14) Окружность с центром 
вписана в трапецию ABCD и касается меньшего основания ВС в точке N, а боковой стороны АВ – в точке M. Найдите площадь треугольника BOC, если MA=25, МВ=9 и CD=50.
№У32.15) В треугольнике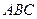 
расстояние от центра описанной окружности до стороны 
равно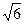 
, угол 
равен 
, угол 
равен 
. Найдите длину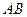 
.
№У32.16) В угол вписана окружность. Точки касания соединены хордой, длина которой 3см. К окружности проведены две касательные, параллельные хорде. Найти длину меньшего основания полученной трапеции и её площадь, если боковая сторона этой трапеции равна 48см.
Ответы к главе 32.
№32.11) 15; №32.12)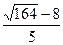 
; №32.13) 
; №32.14) 105; №32.15) 6; №32.16) 
.