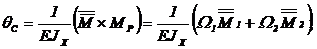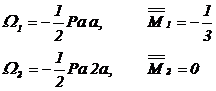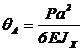Определение механических характеристик.
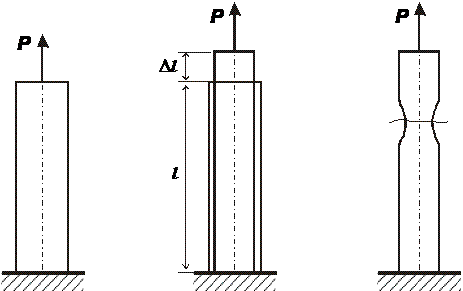Испытания на растяжение стального образца. Нагрузка увеличивается постепенно от нуля до значения, при котором происходит разрыв образца.
|
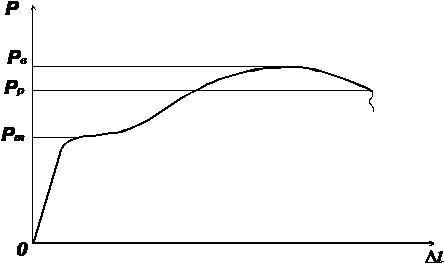Диаграмма растяжения стали (малоуглеродистая сталь):
Рт –нагрузка, при которой началась текучесть;
Рв – наибольшая нагрузка, выдержанная образцом;
Рр –нагрузка, при которой произошел разрыв образца.
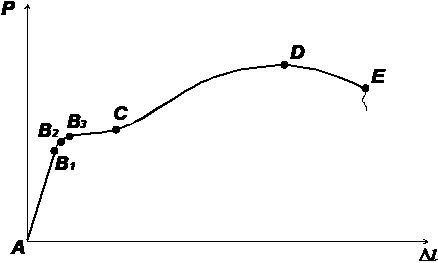
Основные зоны диаграммы:
АВ1 – зона действия закона Гука, деформации пропорциональны нагрузке;
АВ2 – зона упругости, в материале нарастают упругие деформации, пластические деформации пренебрежимо малы;
В3С – зона общей текучести, в материале при постоянной нагрузке по всему объему нарастают пластические деформации;
СD – зона упрочнения, в материале нарастают как пластические, так и упругие деформации, причем для удлинения образца требуется увеличение нагрузки;
DE – зона разрушения или зона местной текучести, материал течет вблизи ослабленного сечения, происходит образование шейки - местного сужения образца, затем происходит разрыв по месту образования шейки.
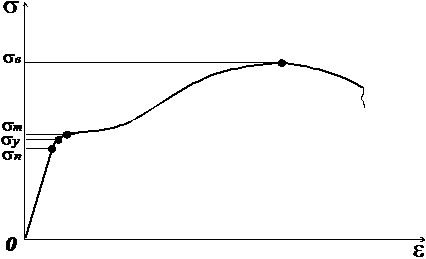
Диаграмма растяжения стали в напряжениях:
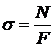
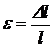
Механические характеристики материала:
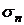- предел пропорциональности, наивысшее напряжение, при котором выполняется закон Гука 
;
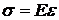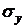- предел упругости, наивысшее напряжение, при котором в материале нарастают только упругие деформации, пластические деформации пренебрежимо малы;
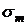- предел текучести, напряжение, при котором материал начинает течь, т.е. происходит рост пластических деформаций при постоянной нагрузке;
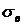- предел прочности, напряжение, соответствующее наибольшей нагрузке, которую материал выдержал до разрушения.
Диаграмма растяжения чугуна (хрупкого материала):
Разрушение происходит в зоне упругих деформаций, явление текучести отсутствует, единственная механическая характеристика – предел прочности .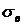
Кручение
В поперечных сечениях действуют:
внутренний силовой фактор – крутящий момент М (Н × м, кН × м),
касательное напряжение t (Па, МПа), вектор касательного напряжения лежит в плоскости поперечного сечения:
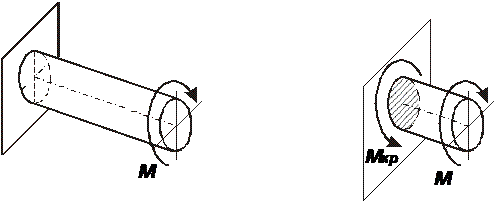
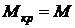
Напряжения в каждой точке сечения перпендикулярны радиусу проведенному в эту точку и пропорциональны расстоянию от точки до центра сечения. Наибольшие напряжения на поверхности скручиваемого стержня.
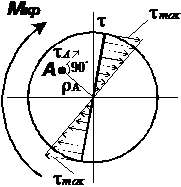
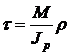
r – радиус-вектор точки сечения, в которой определяется напряжение,
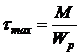
Jp, Wp – геометрические характеристики сечения.
Геометрические характеристики круглого сечения,
используемые в расчетах на кручение
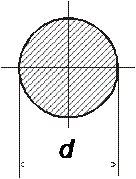Полярный момент инерции сечения:
 |
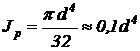, (м4).
Полярный момент сопротивления сечения:
 |
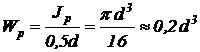, (м3).
Деформации при кручении:
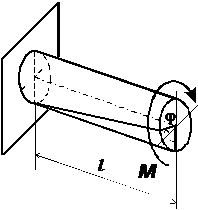
Угол закручивания Dj (рад) – угол, на который повернется рассматриваемое сечение относительно неподвижного:
 |
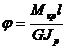
относительный угол закручивания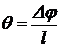 
(рад/м).
Закон Гука при кручении:
,
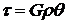G – модуль сдвига, для стали G=8 × 104 МПа.
Условие прочности при кручении:
,
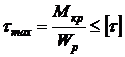допускаемое касательное напряжение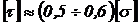 
.
Из условия прочности можно определить радиус круглого сечения: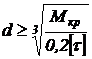 
Условие жесткости при кручении:
,
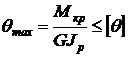допускаемый относительный угол закручивания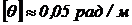 
.
Из условия жесткости можно определить радиус круглого сечения: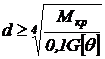 
Изгиб (плоский изгиб)
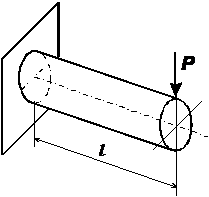
В поперечных сечениях действуют:
внутренние силовые факторы – поперечная сила Q (Н, кН); изгибающий момент М (Н × м, кН × м),
нормальное напряжение s от действия момента, касательное напряжение t от действия поперечной силы (как правило t << s):
Консольная балка (один участок нагружения):
Рассмотрим равновесие отсеченной части балки
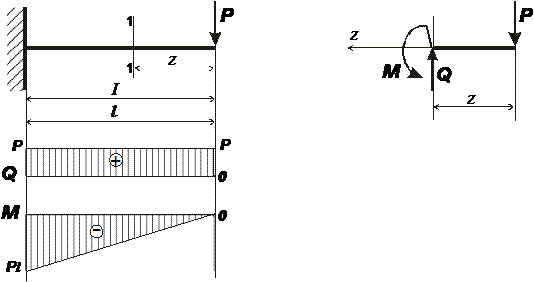
0 £ z £ l
Опасное сечение - в заделке, где момент наибольший по абсолютной величине.
Правило знаков для поперечных сил и изгибающих моментов:
Поперечная сила в сечении положительна, если внешние нагрузки вращают отсеченную часть балки по часовой стрелке.
Изгибающий момент в сечении положителен, если внешние нагрузки стремятся сжать верхние волокна балки.
Нормальные напряжения по высоте поперечного сечения балки изменяются по линейному закону, на верхней и нижней границах сечения напряжения максимальны (правило знаков – при растяжении продольных волокон балки напряжения положительны, при сжатии – отрицательны), ось х – нейтральная ось сечения, на ней напряжения равны нулю:
 |  |
; 
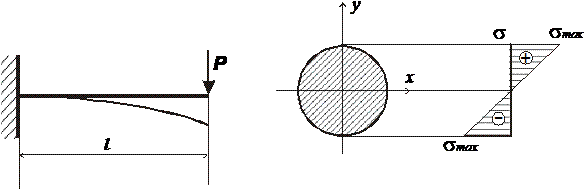
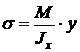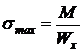
Jx, Wx – геометрические характеристики сечения
Геометрические характеристики сечений, используемые в расчетах на изгиб
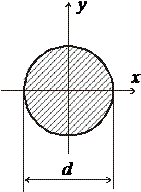Круглое сечение
Осевой момент инерции сечения:
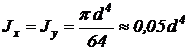, (м4).
Осевой момент сопротивления сечения:
 |
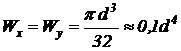, (м3).
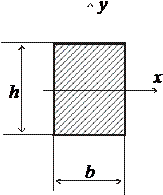Прямоугольное сечение
Осевой момент инерции сечения:
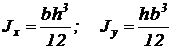, (м4).
Осевой момент сопротивления сечения:
 |
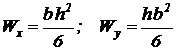, (м3).
Условие прочности при изгибе:
,
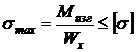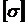- допускаемое напряжение, выбирается так же, как при растяжении-сжатии.
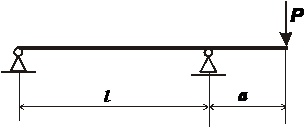Шарнирно опертая балка:
Построим эпюры внутренних силовых факторов и подберем прямоугольное сечение.
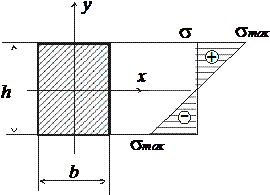
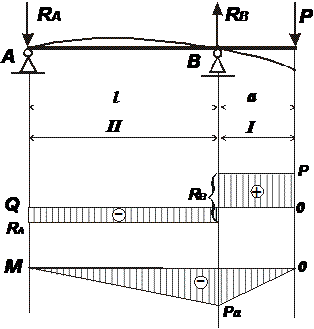
Определим вертикальные реакции в шарнирных опорах RA, RB. Уравнения равновесия:
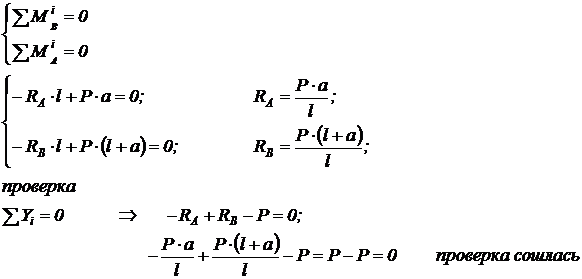
Определим поперечные силы и изгибающие моменты на каждом участке нагружения, пользуясь методом сечений.
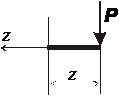I участок: 
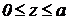(справа)
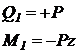
Тогда на границах участка
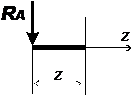II участок: 
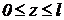(слева)
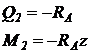
Тогда на границах участка
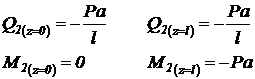
Опасным является сечение, где момент принимает наибольшее значение,
.
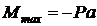Так как в опасном сечении момент отрицательный, верхние волокна растянуты, нижние - сжаты.
Условие прочности
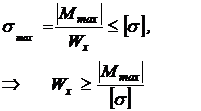
Подберем прямоугольное сечение, пусть h=2b, P=1 кН, а=0,2 м, [s]=100 МПа, тогда
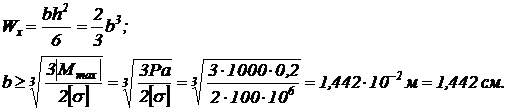
Определение перемещений при изгибе методом Верещагина
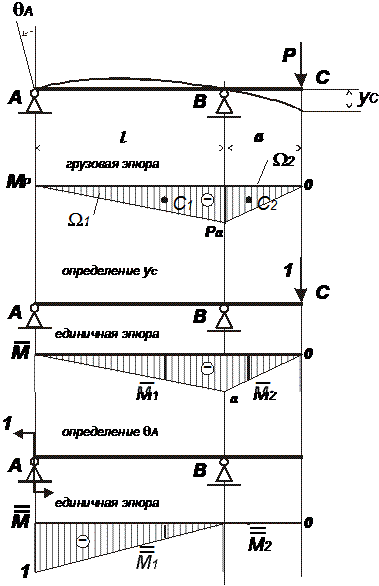
Определим прогиб в сечении С yC
1. Строим эпюру от внешней нагрузки (грузовая эпюра).
2. Строим эпюру от безразмерной единичной силы, приложенной в сечении С (единичная эпюра). Направление единичной силы – предположительное направление вертикального перемещения сечения.
3. Перемножаем эпюры (площади грузовой эпюры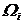 
умножаем на ординаты единичной 
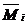под центрами тяжести грузовой 
)
.
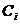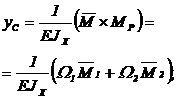
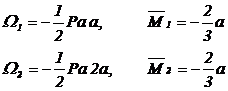
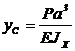Определим угол поворота сечения А qA
1. Строим эпюру от внешней нагрузки (грузовая эпюра).
2. Строим эпюру от безразмерного единичного момента, приложенного в сечении А (единичная эпюра). Направление единичного момента – предположительное направление поворота сечения.
3. Перемножаем эпюры (площади грузовой эпюры 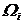умножаем на ординаты единичной 
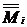под центрами тяжести грузовой )
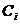